Question:
(a). Approximate f by a Taylor polynomial with degree at the number a.
(b). Graph f and Tn on a common screen.
(c). Use Taylor’s Inequality to estimate the accuracy of the approximation f (X) = Tn(x) when lies in the given interval.
(d). Check your result in part (c) by graphing |Rn(x)|.
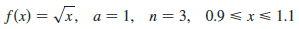
Transcribed Image Text:
f(x) = Vx, a = 1, n= 3, 0.9
> For the limit illustrate Definition 1 by finding values of that correspond to e = 0.5 and e = 0.1 e* - 1 lim - 1
> Find a power series representation for the function and determine the interval of convergence. x? f(x) = .3 a - x .3
> (a). Use the binomial series to expand 1/ √1 - x2. (b). Use part (a) to find the Maclaurin series for sin-1 x.
> Use the Maclaurin series for sin x to compute si 30 correct to five decimal places.
> Use the Maclaurin series for ex to calculate e-0.2 correct to five decimal places.
> Find the Maclaurin series of f (by any method) and its radius of convergence. Graph f and its first few Taylor polynomials on the same screen. What do you notice about the relationship between these polynomials and f? f(x) = In(1 + x²)
> If the radius of convergence of the power series ∑∞n=0cnxn is 10, what is the radius of convergence of the series ∑∞n=0ncnxn-1? Why?
> Let fn(x) = (sin nx)/n2. Show that the series ∑fn(x) converges for all values of x but the series of derivatives ∑fn'(x) diverges when x = 2nπ, an integer. For what values of x does the series ∑fn"(x) converge?
> Find the Maclaurin series of f (by any method) and its radius of convergence. Graph f and its first few Taylor polynomials on the same screen. What do you notice about the relationship between these polynomials and f? f(x) = cos(x²)
> Use a Maclaurin series in Table 1 to obtain the Maclaurin series for the given function. sin x if x+0 f(x) = if x = 0
> Find the area of the region enclosed by one loop of the curve. r= 4 sin 30
> Use a Maclaurin series in Table 1 to obtain the Maclaurin series for the given function. .2 f(x) = /2 + x
> Use a Maclaurin series in Table 1 to obtain the Maclaurin series for the given function. f(x) = - V4 + x? %3D
> The resistivity of a conducting wire is the reciprocal of the conductivity and is measured in units of ohm-meters (Ωm). The resistivity of a given metal depends on the temperature according to the equation where is the temperature i
> An electric dipole consists of two electric charges of equal magnitude and opposite sign. If the charges are q and -q and are located at a distance d from each other, then the electric field E at the point P in the figure is E = q/D2 –
> Use a Maclaurin series in Table 1 to obtain the Maclaurin series for the given function. f(x) — е* + 2е- e
> Use a Maclaurin series in Table 1 to obtain the Maclaurin series for the given function. f(x) = e + e2*
> Suppose you know that and the Taylor series of f centered at 4 converges to f (x) for all in the interval of convergence. Show that the fifth degree Taylor polynomial approximates f (5) with error less than 0.0002. (-1)*n! f®(4) 3"(n 1)
> Use a Maclaurin series in Table 1 to obtain the Maclaurin series for the given function. f(x) = sin 7x
> Use the binomial series to expand the function as a power series. State the radius of convergence. (1 – x)-/3
> Use the Alternating Series Estimation Theorem or Taylor’s Inequality to estimate the range of values of for which the given approximation is accurate to within the stated error. Check your answer graphically. x (| error |< 6 :0.01)
> Find the area of the region enclosed by one loop of the curve. r= sin 20
> Use the binomial series to expand the function as a power series. State the radius of convergence. 1 (1 + x)* 4
> Use the binomial series to expand the function as a power series. State the radius of convergence. + x
> Use the information from Exercise 14 to estimate sin 380 correct to five decimal places. Exercise 14: f(x) = sin x, a = "/6, n= 4, 0<x</3
> Use the information from Exercise 5 to estimate cos 800 correct to five decimal places. Exercise 5: Find the Taylor polynomial T3(x) for the function f at the number a. Graph f and T3 on the same screen. = cos x, a = T/2 1 = 7/2
> (a). Approximate f by a Taylor polynomial with degree n at the number a. (b). Use Taylor’s Inequality to estimate the accuracy of the approximation f (x) ≈ Tn (x) when x lies in the given interval. (c). Check your resu
> (a). Approximate f by a Taylor polynomial with degree n at the number a. (b). Use Taylor’s Inequality to estimate the accuracy of the approximation f (x) ≈ Tn (x) when x lies in the given interval. (c). Check your resu
> (a). Approximate f by a Taylor polynomial with degree n at the number a. (b). Use Taylor’s Inequality to estimate the accuracy of the approximation f (x) ≈ Tn (x) when x lies in the given interval. (c). Check your resu
> (a). Approximate f by a Taylor polynomial with degree n at the number a. (b). Use Taylor’s Inequality to estimate the accuracy of the approximation f (x) ≈ Tn (x) when x lies in the given interval. (c). Check your resu
> (a). Approximate f by a Taylor polynomial with degree n at the number a. (b). Use Taylor’s Inequality to estimate the accuracy of the approximation f (x) ≈ Tn (x) when x lies in the given interval. (c). Check your resu
> (a). Approximate f by a Taylor polynomial with degree n at the number a. (b). Use Taylor’s Inequality to estimate the accuracy of the approximation f (x) ≈ Tn (x) when x lies in the given interval. (c). Check your resu
> Graph the curve and find the area that it encloses. r= 2 sin e + 3 sin 90
> (a). Approximate f by a Taylor polynomial with degree n at the number a. (b). Use Taylor’s Inequality to estimate the accuracy of the approximation f (x) ≈ Tn (x) when x lies in the given interval. (c). Check your resu
> (a). Approximate f by a Taylor polynomial with degree n at the number a. (b). Use Taylor’s Inequality to estimate the accuracy of the approximation f (x) ≈ Tn (x) when x lies in the given interval. (c). Check your resu
> Find the Maclaurin series for f (x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn (x) → 0.] Also find the associated radius of convergence. f(x) = xe хе
> Find the Maclaurin series for f (x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn (x) → 0.] Also find the associated radius of convergence. f(x) = e5=
> Find the Taylor polynomial T3(x) for the function f at the number a. Graph f and T3 on the same screen. f(x) = tan-'x, a = 1
> Find the Taylor polynomial T3(x) for the function f at the number a. Graph f and T3 on the same screen. f(x) %3D хе -2:, а %3D 0 = xe a = 0
> Find the Taylor polynomial T3(x) for the function f at the number a. Graph f and T3 on the same screen. f(x) In x a = 1
> Find the Taylor polynomial T3(x) for the function f at the number a. Graph f and T3 on the same screen. = cos x, a = T/2 1 = 7/2
> Find the Taylor polynomial T3(x) for the function f at the number a. Graph f and T3 on the same screen. f(x) = x + e, a=0
> Find the Taylor polynomial T3(x) for the function f at the number a. Graph f and T3 on the same screen. f(x) = 1/x, a = 2
> Graph the curve and find the area that it encloses.
> (a). Find the Taylor polynomials up to degree 3 for f (x) = 1/x centered at a = 1. Graph f and these polynomials on a common screen. (b). Evaluate f and these polynomials at x = 0.9 and 1.3. (c). Comment on how the Taylor polynomials converge to f (x).
> (a). Find the Taylor polynomials up to degree 6 for f (x) = cos x centered at a = 0. Graph f and these polynomials on a common screen. (b). Evaluate f and these polynomials at x = π/4, π/2, and π. (c). Comment on how the Taylor polynomials converge to f
> Use series to evaluate the following limit. limx→0 sin x – x/ x3
> (a). Approximate f by a Taylor polynomial with degree at the number a. (b). Graph f and Tn on a common screen. (c). Use Taylor’s Inequality to estimate the accuracy of the approximation f (X) = Tn(x) when lies in the given interval. (d)
> Use series to approximate f10√1 + x4, dx correct to two decimal places.
> Evaluate f ex/x dx as an infinite series.
> Find the Maclaurin series for f and its radius of convergence. You may use either the direct method (definition of a Maclaurin series) or known series such as geometric series, binomial series, or the Maclaurin series for ex, sin x, and tan-1x. f(x)
> Find the Maclaurin series for f and its radius of convergence. You may use either the direct method (definition of a Maclaurin series) or known series such as geometric series, binomial series, or the Maclaurin series for ex, sin x, and tan-1x. f(x)
> Find the Maclaurin series for f and its radius of convergence. You may use either the direct method (definition of a Maclaurin series) or known series such as geometric series, binomial series, or the Maclaurin series for ex, sin x, and tan-1x. f(x)
> Sketch the curve and find the area that it encloses. r = 2 + cos 2θ
> Find the Maclaurin series for f and its radius of convergence. You may use either the direct method (definition of a Maclaurin series) or known series such as geometric series, binomial series, or the Maclaurin series for ex, sin x, and tan-1x. f(x)
> Find the Maclaurin series for f and its radius of convergence. You may use either the direct method (definition of a Maclaurin series) or known series such as geometric series, binomial series, or the Maclaurin series for ex, sin x, and tan-1x. f(x)
> Find the Maclaurin series for f and its radius of convergence. You may use either the direct method (definition of a Maclaurin series) or known series such as geometric series, binomial series, or the Maclaurin series for ex, sin x, and tan-1x. f(x)
> Find the Maclaurin series for f and its radius of convergence. You may use either the direct method (definition of a Maclaurin series) or known series such as geometric series, binomial series, or the Maclaurin series for ex, sin x, and tan-1x. f(x)
> Find the Maclaurin series for f and its radius of convergence. You may use either the direct method (definition of a Maclaurin series) or known series such as geometric series, binomial series, or the Maclaurin series for ex, sin x, and tan-1x. x? f
> Find the Taylor series of f (x) = cos x at a = π/3.
> Find the Taylor series of f (x) = sin x at a π/6.
> Find the radius of convergence of the series ∑∞n=1 (2n)!/(n!)2 xn.
> Find the radius of convergence and interval of convergence of the series. 2"(х — 3)" Σ In + 3 00
> Find the radius of convergence and interval of convergence of the series. 2"х — 2)" A-1 (п + 2)!
> Sketch the curve and find the area that it encloses. r = 2 cos 3θ
> Find the radius of convergence and interval of convergence of the series. (x + 2)* Σ n4" 00 n-
> Find the radius of convergence and interval of convergence of the series. x' E (-1)" - n25" ,2.
> Prove that if the series ∑∞n=1 an is absolutely convergent, then the series ∑∞n=1 (n + 1/n)an is also absolutely convergent.
> (a). Show that the series ∑∞n=1nn/(2n)! is convergent. (b). Deduce that limn→∞ nn/(2n)! = 0.
> Use the sum of the first eight terms to approximate the sum of the series∑∞n=1 (2 + 5n)-1. Estimate the error involved in this approximation.
> (a). Find the partial sum s5 of the series ∑∞n=1 1/n6 and estimate the error in using it as an approximation to the sum of the series. (b). Find the sum of this series correct to five decimal places.
> Find the sum of the series ∑∞n=1 (-1)n+1 /n5 correct to four decimal places.
> For what values of does the series ∑∞n=1(ln x)n converge?
> Express the repeating decimal as a 1.2345345345… fraction.
> Find the sum of the series. 1 – e + e2/2! + e3/3! + e4/4! - …
> Sketch the region in the plane consisting of points whose polar coordinates satisfy the given conditions. 2 <rs 5, 37/4 < 0 < 5T/4
> Find the sum of the series. ∑∞n=1 [tan-1 (n + 1) – tan-1 n]
> Find the sum of the series. ∑∞n=1 (-1)n πn/32n (2n)!
> Find the sum of the series. ∑∞n=1 (-3)n-1/23n
> Determine whether the series is convergent or divergent. ∑∞n=1 (-5)2n/n29n
> Determine whether the series is convergent or divergent. ∑∞n=1 1 ∙ 3 ∙5 ∙ ∙∙∙ (2n – 1)/5nn!
> Determine whether the series is convergent or divergent. ∑∞n=1 cos 3n/1 + (1.2)n
> Determine whether the series is convergent or divergent. ∑∞n=1 (-1)n-1 √n/n + 1
> Determine whether the series is convergent or divergent. ∑∞n=1 ln (n/3m + 1)
> Determine whether the series is convergent or divergent. ∑∞n=1 1/n √ln n
> Determine whether the series is convergent or divergent. ∑∞n=1 (-1)n/√n + 1
> Sketch the curve and find the area that it encloses. r2 = 4 cos 2θ
> Determine whether the series is convergent or divergent. ∑∞n=1 n3/5n
> Determine whether the series is convergent or divergent. ∑∞n=1 n2 +1/n3 + 1
> Determine whether the series is convergent or divergent. ∑∞n=1 n/n3 + 1
> A sequence is defined recursively by the equations a1 = 1, an+1 = 1/3(an + 4). Show that {an} is increasing and an < 2 for all n. Deduce that {an} is convergent and find its limit.
> Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. {(1 + 3/n)tr}
> Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. In n an
> Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. n sin n an ,2 + 1
> Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. an = = cos(nT/2)
> Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. 3 n a 1+ п? ,2
> Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. 94+1 an 10"
> Find the area of the shaded region. r= sin 20
> Determine whether the sequence is convergent or divergent. If it is convergent, find its limit. 2 + n3 1+ 2n3
> The force due to gravity on an object with mass m at a height above the surface of the earth is F = mgR2/ (R + h)2 where R is the radius of the earth and is the acceleration due to gravity. (a). Express F as a series in powers of h/R. (b). Observe that i

