Question: A clinical study was conducted to see
A clinical study was conducted to see whether an antibody called denosumab is effective in treatment of osteoporosis of postmenopausal women, as reported in the article “Denosumab in Postmenopausal Women with Low Bone Mineral Density (New England Journal of Medicine, Vol. 354, No. 8, pp. 821–831) by M. McClung et al. Postmenopausal women with osteoporosis were randomly assigned into groups that received either a placebo, or a six-month regimen of Denosumab at doses of 14 mg, 60 mg, 100 mg, or 210 mg. The following table provides summary statistics for the body-mass indexes (BMI) of the women in each treatment group.
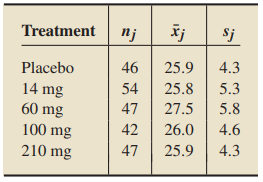
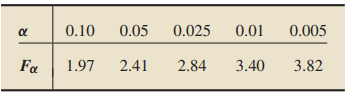
At the 10% significance level, do the data provide sufficient evidence to conclude that a difference exists in mean BMI for women in the five different treatment groups? Note: For the degrees of freedom in this exercise:
> We repeat the data and specify an alternative hypothesis for a correlation t-test. For each exercise, decide, at the 10% significance level, whether the data provide sufficient evidence to reject the null hypothesis in favor of the alternative hypothesis
> We repeat the data and specify an alternative hypothesis for a correlation t-test. For each exercise, decide, at the 10% significance level, whether the data provide sufficient evidence to reject the null hypothesis in favor of the alternative hypothesis
> We repeat the data and specify an alternative hypothesis for a correlation t-test. For each exercise, decide, at the 10% significance level, whether the data provide sufficient evidence to reject the null hypothesis in favor of the alternative hypothesis
> We repeat the data and provide the sample regression equations. a. Determine the standard error of the estimate. b. Construct a residual plot. c. Construct a normal probability plot of the residuals. yˆ = 2 + x
> We repeat the data and specify an alternative hypothesis for a correlation t-test. For each exercise, decide, at the 10% significance level, whether the data provide sufficient evidence to reject the null hypothesis in favor of the alternative hypothesis
> We repeat the data and specify an alternative hypothesis for a correlation t-test. For each exercise, decide, at the 10% significance level, whether the data provide sufficient evidence to reject the null hypothesis in favor of the alternative hypothesis
> If two variables are linearly correlated, one of the variables tends to decrease as the other increases.
> If two variables are positively linearly correlated, one of the variables tends to increase as the other.
> If ρ = 0, then the two variables under consideration are linearly.
> We have presented simple qualitative data set for practicing the concepts. For data set, a. determine a frequency distribution. b. obtain a relative-frequency distribution. c. draw a pie chart. d. construct a bar chart.
> Is ρ a parameter or a statistic? What about r? Explain your answers.
> Suppose that, for a sample of pairs of observations from two variables, the linear correlation coefficient, r, is negative. Does this result necessarily imply that the variables are negatively linearly correlated? Explain.
> Suppose that, for a sample of pairs of observations from two variables, the linear correlation coefficient, r, is positive. Does this result necessarily imply that the variables are positively linearly correlated? Explain.
> Identify the statistic used to estimate the population linear correlation coefficient.
> Refer to the confidence interval and prediction interval formulas. a. Explain why, for a fixed confidence level, the margin of error for the estimate of the conditional mean of the response variable increases as the value of the predictor variable moves
> Figure shows three residual plots and a normal probability plot of residuals. For each part, decide whether the graph suggests violation of one or more of the assumptions for regression inferences. Explain your answers.
> Refer to the data on age and price of a sample of 11 Orions. a. For each age between 2 and 7 years, obtain a 95% confidence interval for the mean price of all Orions of that age. Plot the confidence intervals against age and discuss your results. b. Dete
> The data for age and body fat of 18 randomly selected adults are on the WeissStats site. Specified value of the predictor variable: 30 years. Use the technology of your choice to do the following tasks. a. Decide whether you can reasonably apply the cond
> The data for volume, in cubic feet, and diameter at breast height, in inches, of 70 shortleaf pines are on the WeissStats site. Specified value of the predictor variable: 11 inches. Use the technology of your choice to do the following tasks. a. Decide w
> The data for estriol levels of pregnant women and birth weights of their children are on the WeissStats site. Specified value of the predictor variable: 18 mg/24 hr. Use the technology of your choice to do the following tasks. a. Decide whether you can r
> We have presented simple qualitative data set for practicing the concepts. For data set, a. determine a frequency distribution. b. obtain a relative-frequency distribution. c. draw a pie chart. d. construct a bar chart.
> The data from Exercise 14.41 for gas mileage and engine displacement of 121 vehicles are on the WeissStats site. Specified value of the predictor variable: 3.0 L. Use the technology of your choice to do the following tasks. a. Decide whether you can reas
> The data for shell thickness and concentration of PCBs of 60 Anacapa pelican eggs are on the WeissStats site. Specified value of the predictor variable: 220 ppm. Use the technology of your choice to do the following tasks. a. Decide whether you can reaso
> The data for average high and low temperatures in January of a random sample of 50 cities are on the WeissStats site. Specified value of the predictor variable: 55◦F. Use the technology of your choice to do the following tasks. a. Decide whether you can
> The data for home size (in square feet) and assessed value (in thousands of dollars) for the same homes as in Exercise 14.101 are on the WeissStats site. Specified value of the predictor variable: 3000 sq. ft. Use the technology of your choice to do the
> The data for lot size (in acres) and assessed value (in thousands of dollars) of a sample of homes in a particular area are on the WeissStats site. Specified value of the predictor variable: 2.5 acres. Use the technology of your choice to do the followin
> The data on domestic and overseas grosses for a random sample of 50 movies are on the WeissStats site. Specified value of the predictor variable: $100 million. Use the technology of your choice to do the following tasks. a. Decide whether you can reasona
> Figure shows three residual plots and a normal probability plot of residuals. For each part, decide whether the graph suggests violation of one or more of the assumptions for regression inferences. Explain your answers. Answer: (a) The graph does not
> Suppose that x and y are predictor and response variables, respectively, of a population. Consider the population that consists of all members of the original population that have a specified value of the predictor variable. The distribution, mean, and s
> Find the required F -values. For an F-curve with df = (20, 21), find a. F0.01. b. F0.05. c. F0.10.
> Find the required F -values. An F-curve has df = (12, 5). In each case, find the F-value having the specified area to its right. a. 0.01 b. 0.05 c. 0.005
> Explain the meaning of a. qualitative variable. b. discrete, quantitative variable. c. continuous, quantitative variable.
> Refer to Exercise 13.74. Suppose that you have obtained a 95% confidence interval for each of the two differences, μ1 − μ2 and μ1 − μ3. Can you be 95% confident of both results simultaneously, that is, that both differences are contained in their corresp
> Refer to Exercise 13.55. a. Find and interpret a 95% confidence interval for the mean monthly rent of newly completed apartments in the Midwest. b. Find and interpret a 95% confidence interval for the difference between the mean monthly rents of newly co
> We discussed how to use summary statistics (sample sizes, sample means, and sample standard deviations) to conduct a one-way ANOVA. a. Verify the formula presented there for obtaining the mean of all the observations, namely, b. Show that, if all the sam
> Use the technology of your choice to do the following tasks. a. Obtain individual normal probability plots and the standard deviations of the samples. b. Perform a residual analysis. c. Use your results from parts (a) and (b) to decide whether conducting
> Use the technology of your choice to do the following tasks. a. Obtain individual normal probability plots and the standard deviations of the samples. b. Perform a residual analysis. c. Use your results from parts (a) and (b) to decide whether conducting
> Use the technology of your choice to do the following tasks. a. Obtain individual normal probability plots and the standard deviations of the samples. b. Perform a residual analysis. c. Use your results from parts (a) and (b) to decide whether conducting
> Find the required F -values. An F-curve has df = (24, 30). In each case, find the F-value having the specified area to its right. a. 0.05 b. 0.01 c. 0.025
> Use the technology of your choice to do the following tasks. a. Obtain individual normal probability plots and the standard deviations of the samples. b. Perform a residual analysis. c. Use your results from parts (a) and (b) to decide whether conducting
> Use the technology of your choice to do the following tasks. a. Obtain individual normal probability plots and the standard deviations of the samples. b. Perform a residual analysis. c. Use your results from parts (a) and (b) to decide whether conducting
> Use the technology of your choice to do the following tasks. a. Obtain individual normal probability plots and the standard deviations of the samples. b. Perform a residual analysis. c. Use your results from parts (a) and (b) to decide whether conducting
> Answer true or false to each of the statements in parts (a) and (b), and explain your reasoning. a. Two data sets that have identical frequency distributions have identical relative-frequency distributions. b. Two data sets that have identical relative-f
> In the article by P. Ridker et al. titled “A Randomized Trial of Low-dose Aspirin in the Primary Prevention of Cardiovascular Disease in Women” (New England Journal of Medicine, Vol. 352, pp. 1293–1304), the researchers noted that “We randomly assigned 3
> In the article “Comparison of the Atkins, Ornish, Weight Watchers, and Zone Diets for Weight Loss and Heart Disease Risk Reduction” (Journal of the American Medical Association, Vol. 293, No. 1, pp. 43 53), M. Dansinger et al. conducted a randomized tria
> An article by J. Puranen of the Department of Statistics, University of Helsinki, discussed a classic study on several variables of seven different species of fish caught in Lake Laengelmaevesi, Finland. On the WeissStats site, we present the data on wei
> Nielsen Media Research collects information on daily TV viewing time, in hours, and publishes its findings in Time Spent Viewing. The WeissStats site provides data on daily viewing times of independent simple random samples of men, women, teens, and chil
> The National Association of Colleges and Employers(NACE) conducts surveys on salary offers to college graduates by field and degree. Results are published in Salary Survey. The following table provides summary statistics for starting salaries, in thousan
> Entanglement of marine mammals in fishing gear is a global issue and a significant threat to minke whales, in particular. In the article “Fishing Gears Involved in Entanglements of Minke Whales (Balaenoptera acutorostrata) in the East Sea of Korea” (Mari
> Considerable controversy exists over whether long-term neurodevelopment is affected by nutritional factors in early life. A. Lucas and R. Morley summarized their findings on that question for preterm babies in the publication “Breast Milk and Subsequent
> An F-curve has df = (8, 19). What is the number of degrees of freedom for the: a. denominator? b. numerator?
> In a study by J. Zeng et al., three materials for making artificial teeth—Endura, Duradent, and Duracross—were tested for hardness. Their results were published as the paper “In Vitro Wear Resistance of Three Types of Composite Resin Denture Teeth” (Jour
> In a study by J. Zeng et al., three materials for making artificial teeth—Endura, Duradent, and Duracross—were tested for wear. Their results were published as the paper “In Vitro Wear Resistance of Three Types of Composite Resin Denture Teeth” (Journal
> Explain the difference between a. frequency and relative frequency. b. percentage and relative frequency.
> Rock Sparrows breeding in northern Italy are the subject of a long-term ecology and conservation study due to their wide variety of breeding patterns. Both males and females have a yellow patch on their breasts that is thought to play a significant role
> The U.S. Geological Survey, in cooperation with the Florida Department of Environmental Protection, investigated the effects of waste disposal practices on ground water quality at five poultry farms in north-central Florida. At one site, they drilled fou
> The U.S. Census Bureau collects data on monthly rents of newly completed apartments and publishes the results in Current Housing Reports. Independent random samples of newly completed apartments in the four U.S. regions yielded the data on monthly rents,
> In the publication “How Often Do Fishes ‘Run on Empty’?” (Ecology, Vol. 83, No 8, pp. 2145–2151), D. Arrington et al. examined almost 37,000 fish of 254 species from the waters of Africa, South and Central America, and North America to determine the perc
> Consumer Reports publishes reviews and comparisons of products based on results from its laboratory. Data from their website gave the following table for battery lives, in hours, for samples of laptops made by four different computer companies. The four
> Permeation sampling is a method of sampling air in buildings for pollutants. It can be used over a long period of time and is not affected by humidity, air currents, or temperature. In the paper “Calibration of Permeation Passive Samplers With Silicone M
> In the article “Using EDE, ANOVA and Regression to Optimize Some Microbiology Data” (Journal of Statistics Education, Vol. 12, No. 2, online), N. Binnie analyzed bacteria culture data collected by G. Cooper at the Auckland University of Technology. Five
> We considered two hypothetical examples to explain the logic behind one-way ANOVA. Now, you are to further examine those examples. a. Perform a one-way ANOVA on the data and compare your conclusion to that stated in the corresponding “What Does it Mean?”
> An F-curve has df = (12, 7). What is the number of degrees of freedom for the: a. numerator? b. denominator?
> Copepods are tiny crustaceans that are an essential link in the estuarine food web. Marine scientists G. Weiss et al. at the Chesapeake Biological Laboratory in Maryland designed an experiment to determine whether dietary lipid (fat) content is important
> What is a frequency distribution of qualitative data and why is it useful?
> Movie fans use the annual Leonard Maltin Movie Guide for facts, cast members, and reviews of more than 21,000 films. The movies are rated from 4 stars (4*), indicating a very good movie, to 1 star (1*), which Leonard Maltin refers to as a BOMB. The follo
> We provide data from independent simple random samples from several populations. a. compute SST, SSTR, and SSE by using the computing formulas. b. compare your results in part (a) for SSTR and SSE where you employed the defining formulas. c. construct a
> We provide data from independent simple random samples from several populations. a. compute SST, SSTR, and SSE by using the computing formulas. b. compare your results in part (a) for SSTR and SSE where you employed the defining formulas. c. construct a
> We provide data from independent simple random samples from several populations. a. compute SST, SSTR, and SSE by using the computing formulas. b. compare your results in part (a) for SSTR and SSE where you employed the defining formulas. c. construct a
> We provide data from independent simple random samples from several populations. a. compute SST, SSTR, and SSE by using the computing formulas. b. compare your results in part (a) for SSTR and SSE where you employed the defining formulas. c. construct a
> We provide data from independent simple random samples from several populations. a. compute SST, SSTR, and SSE by using the computing formulas. b. compare your results in part (a) for SSTR and SSE where you employed the defining formulas. c. construct a
> We provide data from independent simple random samples from several populations. a. compute SST, SSTR, and SSE by using the computing formulas. b. compare your results in part (a) for SSTR and SSE where you employed the defining formulas. c. construct a
> Fill in the missing entries in the partially completed one-way ANOVA tables.
> Fill in the missing entries in the partially completed one-way ANOVA tables.
> A chi-square homogeneity test is to be conducted to decide whether a difference exists among the distributions of a variable of six populations. The variable has five possible values. What are the degrees of freedom for the χ2-statistic?
> Another important type of data is ordinal data, which are data about order or rank given on a scale such as 1, 2, 3, . . . or A, B, C, . . . . Following are several variables. Which, if any, yield ordinal data? Explain your answer. a. Height b. Weight c.
> Using the Fα-notation, identify the F-value having area 0.975 to its left.
> If a variable of two populations has only two possible values, the chi-square homogeneity test is equivalent to a two-tailed test that we discussed in an earlier chapter. What test is that?
> Fill in the missing entries in the partially completed one-way ANOVA tables.
> Fill in the blank: If a variable has only two possible values, the chi-square homogeneity test provides a procedure for comparing several population?
> Fill in the missing entries in the partially completed one-way ANOVA tables.
> State the null and alternative hypotheses for a chi-square homogeneity test a. without using the terms homogeneous and nonhomogeneous. b. using the terms homogeneous and nonhomogeneous.
> In each part, specify what type of analysis you might use. a. To study the effect of one factor on the mean of a response variable b. To study the effect of two factors on the mean of a response variable.
> Consider a variable of several populations. Define the terms homogeneous and nonhomogeneous in this context.
> True or false: If you know any two of the three sums of squares, SST, SSTR, and SSE, you can determine the remaining one. Explain your answer.
> For what purpose is a chi-square homogeneity test used?
> The following table presents information on the Kelley Blue Book’s “10 Best Green Cars of 2013.” Note that mpg and mpge are abbreviations for miles per gallon and miles per gallon equivalent, respectively. Identify the type of data provided by the inform
> State the one-way ANOVA identity, and interpret its meaning with regard to partitioning the total variation in the data.
> Although the chi-square homogeneity test and the chi-square independence test use essentially the same basic procedure, the context of the two tests are quite different. Explain the difference.
> Following are the notations for the three sums of squares. State the name of each sum of squares and the source of variation each sum of squares represents. a. SSE b. SSTR c. SST
> A CNN/USA TODAY poll conducted by Gallup asked a sample of employed Americans the following question: “Which do you enjoy more, the hours when you are on your job, or the hours when you are not on your job?” The responses to this question were cross-tabu
> We stated earlier that a one-way ANOVA test is always right tailed because the null hypothesis is rejected only when the test statistic, F, is too large. Why is the null hypothesis rejected only when F is too large?
> A CNN/USA TODAY poll conducted by Gallup asked a sample of employed Americans the following question: “Which do you enjoy more, the hours when you are on your job, or the hours when you are not on your job?” The responses to this question were cross-tabu
> Suppose that a one-way ANOVA is being performed to compare the means of three populations and that the sample sizes are 10, 12, and 15. Determine the degrees of freedom for the F-statistic.
> A CNN/USA TODAY poll conducted by Gallup asked a sample of employed Americans the following question: “Which do you enjoy more, the hours when you are on your job, or the hours when you are not on your job?” The responses to this question were cross-tabu
> Suppose that the variable under consideration is normally distributed on each of two populations and that the population standard deviations are equal. Further suppose that you want to perform a hypothesis test to decide whether the populations have diff
> Why is the phrase “goodness of fit” used to describe the type of hypothesis test considered in this section?
> The U.S. government’s flagship international educational exchange program, the Fulbright program, is sponsored by the Bureau of Educational and Cultural Affairs. Fulbright’s are awarded based on “academic and leadership potential, providing the opportuni
> Show that, for two populations, MSE = s2p, where s2p is the pooled variance defined in Section 10.2 on page 407. Conclude that √MSE is the pooled sample standard deviation, sp.
> A CNN/USA TODAY poll conducted by Gallup asked a sample of employed Americans the following question: “Which do you enjoy more, the hours when you are on your job, or the hours when you are not on your job?” The responses to this question were cross-tabu

