Question:
(a) Find the average value off on the given interval.
(b) Find c such that fave – f(c)
(c) Sketch the graph of f and a rectangle whose area is the same as the area under the graph of f.
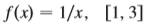
Transcribed Image Text:
f(x) = 1/x, [1, 3]
> A tank full of water has the shape of a paraboloid of revolution as shown in the figure; that is, its shape is obtained by rotating a parabola about a vertical axis. (a) If its height is 4 ft and the radius at the top is 4 ft, find the work required to p
> A 1600-lb elevator is suspended by a 200-ft cable that weighs 10 lb/ft. How much work is required to raise the elevator from the basement to the third floor, a distance of 30 ft?
> (a) The base of a solid is a square with vertices located at (1, 0), (0, 1), (21, 0), and (0, 21). Each cross-section perpendicular to the x-axis is a semicircle. Find the volume of the solid. (b) Show that by cutting the solid of part (a), we can rearra
> The height of a monument is 20 m. A horizontal cross section at a distance x meters from the top is an equilateral triangle with / meters. Find the volume of the monument.
> The base of a solid is the region bounded by the parabolas y = x2 and y = 2 - x2. Find the volume of the solid if the cross-sections perpendicular to the x-axis are squares with one side lying along the base.
> The base of a solid is a circular disk with radius 3. Find the volume of the solid if parallel cross-sections perpendicular to the base are isosceles right triangles with hypotenuse lying along the base.
> Sketch the region enclosed by the given curves and find its area. у 3 sinhx, у —е , х—0, х—2
> Each integral represents the volume of a solid. Describe the solid. 2т (6 — у)(4у — у?) dy
> Each integral represents the volume of a solid. Describe the solid. S T (2 – sin x)² dx
> Let / be the region bounded by the curves y = 1 - x2 and y = x6 - x + 1. Estimate the following quantities. (a) The x-coordinates of the points of intersection of the curves (b) The area of / (c) The volume generated when/is rotated about the x-axis (d)
> Let / be the region bounded by the curves y = tan(x2), x = 1, and y = 0. Use the Midpoint Rule with n = 4 to estimate the following quantities. (a) The area of/ b) The volume obtained by rotating / about the x-axis
> Let / be the region in the first quadrant bounded by the curves y = x3 and y = 2x 2 x2. Calculate the following quantities. (a) The area of / (b) The volume obtained by rotating / about the x-axis (c) The volume obtained by rotating / about the y-axis
> Find the volumes of the solids obtained by rotating the region bounded by the curves y = x and y = x2 about the following lines. (a) The x-axis (b) The y-axis (c) y = 2
> Set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. - y = Vx, y = x²; about y = 2
> Set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. у — соs х, [|x| < п/2, у — %: about.х — п, п/2
> Set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. у %3 tan x, у — х, х — п/3; about the y-axis TT
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. x? – y? = a², x = a + h (where a>0, h > 0); about the y-axis
> Sketch the region enclosed by the given curves and find its area. y = x*, y = 2 - |x| у — х",
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. y = x? + 1, y = 9 – x²; about y = -1
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. x = 0, x = 9 – y²; about x = -1
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. x = 1 + y², y - x – 3; about the y-axis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. _y = 2x, y = x²; about the x-axis %3D
> Find the area of the region bounded by the given curves. у 3 Vx, у— х?, х—2 y
> Find the area of the region bounded by the given curves. у у — х? — 2х sin(тx/2), 2.x y
> Find the area of the region bounded by the given curves. x + y = 0, x = y² + 3y
> Find the area of the region bounded by the given curves. у —1- 2x?, у — \x| y y = |x|
> Find the area of the region bounded by the given curves. у — x, у— —Vx, у—х— 2
> (a) An outfielder fields a baseball 280 ft away from home plate and throws it directly to the catcher with an initial velocity of 100 ft/s. Assume that the velocity v(t) of the ball after t seconds satisfies the differential equation dv/dt − 2 1 10v beca
> Sketch the region enclosed by the given curves and find its area. y = cos x, y=1 – cos x, 0<x<T
> In this problem we calculate the work required for a pitcher to throw a 90-miyh fastball by first considering kinetic energy. Suppose an object of mass m, moving in a straight line, is acted on by a force F = F(s) that depends on its position s. Accordin
> It may surprise you to learn that the collision of baseball and bat lasts only about a thousandth of a second. Here we calculate the average force on the bat during this collision by first computing the change in the ball’s momentum. Th
> Find the average value of the function on the given interval. h(u) — (In u)/и, [1,5]
> Find the average value of the function on the given interval. h(x) cos*x sin x, [0, 7]
> If fave [a, b] denotes the average value of f on the interval [a, b] and a b — с Save[c, b] b — а c - a fave[a, b] fave [a, c] + b — а
> Prove the Mean Value Theorem for Integrals by applying the Mean Value Theorem for derivatives (see Section 4.2) to the function /
> Use the diagram to show that if f is concave upward on [a, b], then a + b fave >f 2 y a +b b a 2.
> Use the result of Exercise 5.5.83 to compute the average volume of inhaled air in the lungs in one respiratory cycle.
> If a freely falling body starts from rest, then its displacement is given by / 2tt2. Let the velocity after a time T be vT. Show that if we compute the average of the velocities with respect to t we g / 2vT, but if we compute the average of the velocit
> In Example 3.8.1 we modeled the world population in the second half of the 20th century by the equation P(t) = 2560e0.017185t. Use this equation to estimate the average world population during this time period.
> Sketch the region enclosed by the given curves and find its area. y = 2x, y=x², 0<x<6
> (a) A cup of coffee has temperature 95°C and takes 30 minutes to cool to 61°C in a room with temperature 20°C. Use Newton’s Law of Cooling (Section 3.8) to show that the temperature of the coffee after t
> The velocity v of blood that flows in a blood vessel with radius R and length l at a distance r from the central axis is where P is the pressure difference between the ends of the vessel and is the viscosity of the blood (see Example 3.7.7). Find the av
> In a certain city the temperature (in °F) t hours after 9 am was modeled by the function Find the average temperature during the period from 9 am to 9 pm. T(1) = 50 + 14 sin 12
> The velocity graph of an accelerating car is shown. (a) Use the Midpoint Rule to estimate the average velocity of the car during the first 12 seconds. (b) At what time was the instantaneous velocity equal to the average velocity? (km/h) 60 40 20 4
> Find the average value off on [0, 8]. 1 4 6. 2.
> Find the numbers b such that the average value of f(x) = 2 + 6x = 3x2 on the interval [0, b] is equal to 3.
> If f is continuous and / show that f takes on the value 4 at least once on the interval [1, 3].
> (a) Find the average value of f on the given interval. (b) Find c such that fave – f(c) (c) Sketch the graph of f and a rectangle whose area is the same as the area under the graph of f. f(x) = 2xe *', [0, 2]
> (a) Find the average value of f on the given interval. (b) Find c such that fave – f(c) (c) Sketch the graph of f and a rectangle whose area is the same as the area under the graph of f. f(x) — [0, п] 2 sin x – sin 2x,
> Sketch the region enclosed by the given curves and find its area. .3 y = x', y=x
> (a) Find the average value of f on the given interval. (b) Find c such that fave – f(c) (c) Sketch the graph of f and a rectangle whose area is the same as the area under the graph of f. S(x) f() — (х — 3)?, [2, 5]
> Shown is the graph of a force function (in newtons) that increases to its maximum value and then remains constant. How much work is done by the force in moving an object a distance of 8 m? FA(N) 30 20 10 1 2 3 4 5 6 7 8 x (m)
> When a particle is located a distance x meters from the origin, a force of / newtons acts on it. How much work is done in moving the particle from x = 1 to x = 2? Interpret your answer by considering the work done from x = 1 to x = 1.5 and from x = 1.5 t
> The Great Pyramid of King Khufu was built of limestone in Egypt over a 20-year time period from 2580 bc to 2560 bc. Its base is a square with side length 756 ft and its height when built was 481 ft. (It was the tallest manmade structure in the world for
> (a) Newton’s Law of Gravitation states that two bodies with masses m1 and m2 attract each other with a force where r is the distance between the bodies and G is the gravitational constant. If one of the bodies is fixed, find the work ne
> Suppose that when launching an 800-kg roller coaster car an electromagnetic propulsion system exerts a force of 5.7x2 + 1.5x newtons on the car at a distance x meters along the track. Use Exercise 31(a) to find the speed of the car when it has traveled 6
> The kinetic energy KE of an object of mass m moving with velocity v is defined as / 2 mv2. If a force f(x) acts on the object, moving it along the x-axis from x1 to x2, the Work-Energy Theorem states that the net work done is equal to the change in kine
> In a steam engine the pressure P and volume V of steam satisfy the equation PV1.4 = k, where k is a constant. (This is true for adiabatic expansion, that is, expansion in which there is no heat transfer between the cylinder and its surroundings.) Use Exe
> When gas expands in a cylinder with radius r, the pressure at any given time is a function of the volume: P − P(V). The force exerted by the gas on the piston (see the figure) is the product of the pressure and the area: F −
> Solve Exercise 24 if the tank is half full of oil that has a density of 900 kg/m3.
> Sketch the region enclosed by the given curves and find its area. y = tan x, y = 2 sin x, -7/3 < x< #/3
> Find the area of the shaded region. yA x= y? – 2 y=1 (x=e' ソニー1
> Suppose that for the tank in Exercise 23 the pump breaks down after 4.7 × 105 J of work has been done. What is the depth of the water remaining in the tank? Data from Exercise 23: A tank is full of water. Find the work required to pump the
> A tank is full of water. Find the work required to pump the water out of the spout. In Exercises 25 and 26 use the fact that water weighs 62.5 lb/ft3. 6 ft 26. 12 ft - f 8 ft 6 ft - 3 ft 10 ft frustum of a cone
> A tank is full of water. Find the work required to pump the water out of the spout. In Exercises 25 and 26 use the fact that water weighs 62.5 lb/ft3. - 3 m - 24. |1 m 2 m 3 m 3 m 8 m
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A spherical water tank, 24 ft in diameter, sits atop a 60 ft tower. The tank is filled by a hose attached to the bottom of the sphere. If a
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. An aquarium 2 m long, 1 m wide, and 1 m deep is full of water. Find the work needed to pump half of the water out of the aquarium. (Use the
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A circular swimming pool has a diameter of 24 ft, the sides are 5 ft high, and the depth of the water is 4 ft. How much work is required to
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A 10-ft chain weighs 25 lb and hangs from a ceiling. Find the work done in lifting the lower end of the chain to the ceiling so that it’s le
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A bucket that weighs 4 lb and a rope of negligible weight are used to draw water from a well that is 80 ft deep. The bucket is filled with 4
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A leaky 10-kg bucket is lifted from the ground to a height of 12 m at a constant speed with a rope that weighs 0.8 kg/m. Initially the bucke
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A chain lying on the ground is 10 m long and its mass is 80 kg. How much work is required to raise one end of the chain to a height of 6 m?
> Sketch the region enclosed by the given curves and find its area. х — у, у— V2 — х, у— 0 2- х, у x =
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A cable that weighs 2 lb/ft is used to lift 800 lb of coal up a mine shaft 500 ft deep. Find the work done.
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A thick cable, 60 ft long and weighing 180 lb, hangs from a winch on a crane. Compute in two different ways the work done if the winch winds
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A heavy rope, 50 ft long, weighs 0.5 lb/ft and hangs over the edge of a building 120 ft high. (a) How much work is done in pulling the rope
> If 6 J of work is needed to stretch a spring from 10 cm to 12 cm and another 10 J is needed to stretch it from 12 cm to 14 cm, what is the natural length of the spring?
> A spring has natural length 20 cm. Compare the work W1 done in stretching the spring from 20 cm to 30 cm with the work W2 done in stretching it from 30 cm to 40 cm. How are W2 and W1 related?
> If the work required to stretch a spring 1 ft beyond its natural length is 12 ft-lb, how much work is needed to stretch it 9 in. beyond its natural length?
> Suppose that 2 J of work is needed to stretch a spring from its natural length of 30 cm to a length of 42 cm. (a) How much work is needed to stretch the spring from 35 cm to 40 cm? (b) How far beyond its natural length will a force of 30 N keep the sprin
> A spring has a natural length of 40 cm. If a 60-N force is required to keep the spring compressed 10 cm, how much work is done during this compression? How much work is required to compress the spring to a length of 25 cm?
> A force of 10 lb is required to hold a spring stretched 4 in. beyond its natural length. How much work is done in stretching it from its natural length to 6 in. beyond its natural length?
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. -у — х*, у— 0, х— 1, х— 2
> Sketch the region enclosed by the given curves and find its area. у — сos пх, у— 4x? — 1 y = 4x² – 1
> Use the method of cylindrical shells to find the volume generated by rotating the region bounded by the given curves about the y-axis. у — Vх, у— 0, х—1
> Let S be the solid obtained by rotating the region shown in the figure about the y-axis. Sketch a typical cylindrical shell and find its circumference and height. Use shells to find the volume of S. Do you think this method is preferable to slicing? Expl
> Let S be the solid obtained by rotating the region shown in the figure about the y-axis. Explain why it is awkward to use slicing to find the volume V of S. Sketch a typical approximating shell. What are its circumference and height? Use shells to find V
> Suppose you make napkin rings by drilling holes with different diameters through two wooden balls (which also have different diameters). You discover that both napkin rings have the same height h, as shown in the figure. (a) Guess which ring has more woo
> Use cylindrical shells to find the volume of the solid. A right circular cone with height h and base radius r
> Use cylindrical shells to find the volume of the solid. The solid torus of Exercise 6.2.63 Data from Exercise 6.2: Let S be the solid obtained by rotating the region shown in the figure about the y-axis. Sketch a typical cylindrical shell and find its
> Use cylindrical shells to find the volume of the solid. A sphere of radius r
> Let T be the triangular region with vertices (0, 0), (1, 0), and (1, 2), and let V be the volume of the solid generated when T is rotated about the line x = a, where a > 1. Express a in terms of V.
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. = X х — (у — 1), х — у — 1; aboutx — -1
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. x = (y – 3)', x = 4; about y = 1
> Sketch the region enclosed by the given curves and find its area. y = у — Vx — 1, х — у— 1 y
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. x? + (y – 1) = 1; about the y-axis
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. y? – x² = 1, y = 2; about the y-axis
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. y? – x? = 1, y = 2; about the x-axis
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. у 3 —х? + 6х — 8, у — 0;B about the x-axis
> The region bounded by the given curves is rotated about the specified axis. Find the volume of the resulting solid by any method. у — —х? + 6х - 8, у — 0;B about the y-axis

