Question: A flask contains a mixture of neon (
A flask contains a mixture of neon (Ne), krypton (Kr), and radon (Rn) gases. Compare (a) the average kinetic energies of the three types of atoms and (b) the root-mean-square speeds. (Hint: Appendix D shows the molar mass (in g/mol) of each element under the chemical symbol for that element.)
Appendix D:
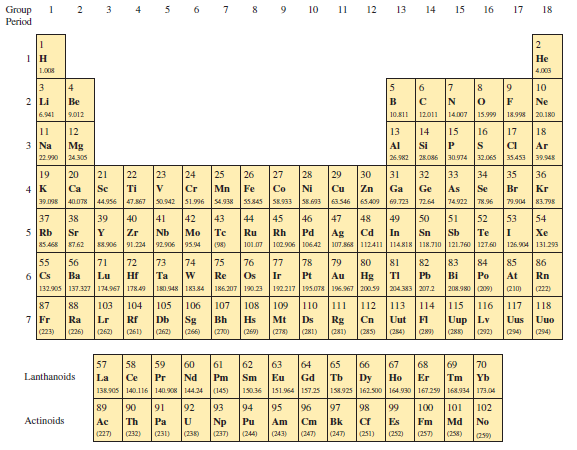
Transcribed Image Text:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Group Period 1 H Не 1.008 4.003 EEPEE 3 8 N 4 6 7 9. 10 2 Li Be B Ne 6.941 9.012 10.811 12.011 14.007 15.999 18.998 20.180 12 Mg 22.990 24.30s 15 IS 11 13 14 16 17 18 3 Na Al Si CI Ar 26.982 28.O6 30.974 32.065 35453 39.945 EEE 20 29 30 21 22 Ti 23 24 25 26 28 33 34 Se Br 19 27 31 32 35 36 4 K 39.098 40.078 44.956 47.867 s0.942 51.996 54.938 55345 S8.933 58.93 63.546 65.409 9.723 72.64 Ca Sc Cr Mn Fe Cu Zn Ga Ge As Kr 74.922 78.96 79.904 83.798 41 42 Nb Мо 91.224 92.906 95.94 47 48 46 Pd EE EEEELEBEEEEEE FE 37 38 5 Rb Sr Y 51 Sb 39 40 43 44 45 49 50 52 53 54 Zr Te Ru Rh Ag 107.868 112411 114818 118.71o 121.760 127.60 Cd In Sn Te I Xe 85.468 87.62 S8.906 (38) 101.07 102.906 10642 126.904 | 131.293 73 74 Та 83 Po 208.980 (209) 55 56 71 72 75 76 77 78 79 80 81 82 84 85 86 6 Cs 132.905 137.327 174.967 178.49 180.948 183.84 Ва Lu Hf Re Os Au Hg Pb Rn 186.207 190.23 192217 195.07s 196.967 200.59 204.383 207.2 210) (222) 87 110 88 Lr (226) 103 104 105 106 107 108 109 111 112 113 114 115 116 117 118 Db Uup Lv (28) 7 Fr Rf Sg (266) Hs Ra Bh Mt Ds Rg Cn Uut FI Uus Uuo (223) (262) (261) (262) (270) (26) (278) (281) (281) (285) (284) (280) (292) (294) (294) 57 58 59 60 Nd 62 Sm 65 Gd 150.36 151.964 1S7.25 64 69 70 Yb 61 63 66 67 68 Lanthanoids La 138.905 140.116 140.908 144.34 (145) Pr Pm Eu Но Er Tm 158.925 162.500 164.930 167.259 168.934 173.04 92 93 94 97 Bk 247) 89 90 91 95 96 98 99 100 101 102 Actinoids Ac No Md (25) Np Pu Am Cm Fm (227) (232) (231) (23) (237) (244) (243) (247) (251) (252) (257) EEEEEEEEEEEEEE
> With the assumption that the air temperature is a uniform 0.0°C, what is the density of the air at an altitude of 1.00 km as a percentage of the density at the surface?
> You live on a busy street, but as a music lover, you want to reduce the traffic noise. (a). If you install special sound reflecting windows that reduce the sound intensity level (in dB) by 30 dB, by what fraction have you lowered the sound intensity 1in
> An experimenter using a gas thermometer found the pressure at the triple point of water (0.01°C) to be 4.80 × 104 Pa and the pressure at the normal boiling point (100°C) to be 6.50 × 104 Pa. (a). Assuming that the pressure varies linearly with temperatu
> A cylindrical tank has a tight-fitting piston that allows the volume of the tank to be changed. The tank originally contains 0.110 m3 of air at a pressure of 0.355 atm. The piston is slowly pulled out until the volume of the gas is increased to 0.390 m3.
> A copper cylinder is initially at 20.0° C. At what temperature will its volume be 0.150% larger than it is at 20.0 °C?
> You are trying to overhear a juicy conversation, but from your distance of 15.0 m, it sounds like only an average whisper of 20.0 dB. How close should you move to the chatterboxes for the sound level to be 60.0 dB?
> The Humber Bridge in England has the world’s longest single span, 1410 m. Calculate the change in length of the steel deck of the span when the temperature increases from -5.0 °C to 18.0 °C.
> A U.S. penny has a diameter of 1.9000 cm at 20.0 C. The coin is made of a metal alloy (mostly zinc) for which the coefficient of linear expansion is 2.6 × 10-5 K-1. What would its diameter be on a hot day in Death Valley (48.0°C)? On a cold night in the
> One of the tallest buildings in the world is the Taipei 101 in Taiwan, at a height of 1671 feet. Assume that this height was measured on a cool spring day when the temperature was 15.5° C. You could use the building as a sort of giant thermometer on a ho
> A constant-volume gas thermometer registers an absolute pressure corresponding to 325 mm of mercury when in contact with water at the triple point. What pressure does it read when in contact with water at the normal boiling point?
> You put a bottle of soft drink in a refrigerator and leave it until its temperature has dropped 10.0 K. What is its temperature change in (a) F° and (b) C° ?
> (a). Calculate the one temperature at which Fahrenheit and Celsius thermometers agree with each other. (b). Calculate the one temperature at which Fahrenheit and Kelvin thermometers agree with each other.
> At a temperature of 27.0C, what is the speed of longitudinal waves in (a). hydrogen (molar mass 2.02 g/mol); (b). helium (molar mass 4.00 g/mol); (c). argon (molar mass 39.9 g/mol)? See Table 19.1 for values of γ. (d). Compare your answer
> (a). By what factor must the sound intensity be increased to raise the sound intensity level by 13.0 dB? (b). Explain why you don’t need to know the original sound intensity.
> The pressure of a gas at the triple point of water is 1.35 atm. If its volume remains unchanged, what will its pressure be at the temperature at which CO2 solidifies?
> Convert the following Kelvin temperatures to the Celsius and Fahrenheit scales: (a). the midday temperature at the surface of the moon (400 K); (b). the temperature at the tops of the clouds in the atmosphere of Saturn (95 K); (c). the temperature at
> (a). Whale communication. Blue whales apparently communicate with each other using sound of frequency 17 Hz, which can be heard nearly 1000 km away in the ocean. What is the wavelength of such a sound in seawater, where the speed of sound is 1531 m/s? (
> A loud factory machine produces sound having a displacement amplitude of 1.00 µm, but the frequency of this sound can be adjusted. In order to prevent ear damage to the workers, the maximum pressure amplitude of the sound waves is limited to 10.0 Pa. Und
> (a). On January 22, 1943, the temperature in Spearfish, South Dakota, rose from -4.0° F to 45.0 °F in just 2 minutes. What was the temperature change in Celsius degrees? (b). The temperature in Browning, Montana, was 44.0° F on January 23, 1916. The nex
> Example 16.1 (Section 16.1) showed that for sound waves in air with frequency 1000 Hz, a displacement amplitude of 1.2 × 10-8 m produces a pressure amplitude of 3.0 × 10-2 Pa. Water at 200C has a bulk modulus of 2.2 × 109 Pa, and the speed of sound in wa
> The hot glowing surfaces of stars emit energy in the form of electromagnetic radiation. It is a good approximation to assume e = 1 for these surfaces. Find the radii of the following stars (assumed to be spherical): (a). Rigel, the bright blue star in t
> The operating temperature of a tungsten filament in an incandescent light bulb is 2450 K, and its emissivity is 0.350. Find the surface area of the filament of a 150-W bulb if all the electrical energy consumed by the bulb is radiated by the filament as
> The emissivity of tungsten is 0.350. A tungsten sphere with radius 1.50 cm is suspended within a large evacuated enclosure whose walls are at 290.0 K. What power input is required to maintain the sphere at 3000.0 K if heat conduction along the supports i
> A spherical pot contains 0.75 L of hot coffee (essentially water) at an initial temperature of 95° C. The pot has an emissivity of 0.60, and the surroundings are at 20.0° C. Calculate the coffee’s rate of heat loss by radiation.
> Sound is detected when a sound wave causes the tympanic membrane (the eardrum) to vibrate. Typically, the diameter of this membrane is about 8.4 mm in humans. (a). How much energy is delivered to the eardrum each second when someone whispers (20 dB) a s
> A picture window has dimensions of 1.40 m × 2.50 m and is made of glass 5.20 mm thick. On a winter day, the temperature of the outside surface of the glass is -20.0 °C, while the temperature of the inside surface is a comfortable 19.5° C. (a). At what r
> You are asked to design a cylindrical steel rod 50.0 cm long, with a circular cross section, that will conduct 190.0 J/s from a furnace at 400.0 °C to a container of boiling water under 1 atmosphere. What must the rod’s diameter be?
> A pot with a steel bottom 8.50 mm thick rests on a hot stove. The area of the bottom of the pot is 0.150 m2. The water inside the pot is at 100.0° C, and 0.390 kg are evaporated every 3.00 min. Find the temperature of the lower surface of the pot, which
> A long rod, insulated to prevent heat loss along its sides, is in perfect thermal contact with boiling water (at atmospheric pressure) at one end and with an ice–water mixture at the other (Fig. E17.62). The rod consists of a 1.00-m sec
> The blood plays an important role in removing heat from the body by bringing this energy directly to the surface where it can radiate away. Nevertheless, this heat must still travel through the skin before it can radiate away. Assume that the blood is br
> An electric kitchen range has a total wall area of 1.40 m2 and is insulated with a layer of fiberglass 4.00 cm thick. The inside surface of the fiberglass has a temperature of 175 C, and its outside surface is at 35.0 C. The fiberglass has a thermal co
> A carpenter builds an exterior house wall with a layer of wood 3.0 cm thick on the outside and a layer of Styrofoam insulation 2.2 cm thick on the inside wall surface. The wood has k = 0.080 W/m ∙ K, and the Styrofoam has k = 0.027 W /m ∙ K. The interior
> Suppose that the rod in Fig. 17.24a is made of copper, is 45.0 cm long, and has a cross-sectional area of 1.25 cm2. Let TH = 100.0 C and TC = 0.0 C. (a). What is the final steady-state temperature gradient along the rod? (b). What is the heat curre
> Two rods, one made of brass and the other made of copper, are joined end to end. The length of the brass section is 0.300 m and the length of the copper section is 0.800 m. Each segment has cross-sectional area 0.00500 m2. The free end of the brass segme
> Calculate the volume of 1.00 mol of liquid water at 20°C (at which its density is 998 kg/m3), and compare that with the volume occupied by 1.00 mol of water at the critical point, which is 56 × 10-6 m3. Water has a molar mass of 18.0 g/mol.
> What must be the stress (F/A) in a stretched wire of a material whose Young’s modulus is Y for the speed of longitudinal waves to equal 30 times the speed of transverse waves?
> The vapor pressure is the pressure of the vapor phase of a substance when it is in equilibrium with the solid or liquid phase of the substance. The relative humidity is the partial pressure of water vapor in the air divided by the vapor pressure of water
> Solid water (ice) is slowly warmed from a very low temperature. (a). What minimum external pressure p1 must be applied to the solid if a melting phase transition is to be observed? Describe the sequence of phase transitions that occur if the applied pre
> For a gas of nitrogen molecules (N2), what must the temperature be if 94.7% of all the molecules have speeds less than (a). 1500 m/s; (b). 1000 m/s; (c). 500 m/s? Use Table 18.2. The molar mass of N2 is 28.0 g/mol. Table 18.2: sa/a v/U rms Fract
> (a). Calculate the specific heat at constant volume of water vapor, assuming the nonlinear triatomic molecule has three translational and three rotational degrees of freedom and that vibrational motion does not contribute. The molar mass of water is 18.0
> (a). Compute the specific heat at constant volume of nitrogen (N2) gas, and compare it with the specific heat of liquid water. The molar mass of N2 is 28.0 g/mol. (b). You warm 1.00 kg of water at a constant volume of 1.00 L from 20.00 C to 30.00 C in a
> Perfectly rigid containers each hold n moles of ideal gas, one being hydrogen (H2) and the other being neon (Ne). If it takes 300 J of heat to increase the temperature of the hydrogen by 2.50 0C, by how many degrees will the same amount of heat raise the
> How much heat does it take to increase the temperature of 1.80 mol of an ideal gas by 50.0 K near room temperature if the gas is held at constant volume and is (a) diatomic; (b) monatomic?
> Smoke particles in the air typically have masses of the order of 10-16 kg. The Brownian motion (rapid, irregular movement) of these particles, resulting from collisions with air molecules, can be observed with a microscope. (a). Find the root mean- squa
> Oxygen (O2) has a molar mass of 32.0 g/mol. What is (a). the average translational kinetic energy of an oxygen molecule at a temperature of 300 K; (b). the average value of the square of its speed; (c). the root-mean-square speed; (d). the momentum of
> (a) A deuteron, 21 H, is the nucleus of a hydrogen isotope and consists of one proton and one neutron. The plasma of deuterons in a nuclear fusion reactor must be heated to about 300 million K. What is the rms speed of the deuterons? Is this a significan
> A 60.0-m-long brass rod is struck at one end. A person at the other end hears two sounds as a result of two longitudinal waves, one traveling in the metal rod and the other traveling in air. What is the time interval between the two sounds? (The speed of
> A container with volume 1.64 L is initially evacuated. Then it is filled with 0.226 g of N2. Assume that the pressure of the gas is low enough for the gas to obey the ideal-gas law to a high degree of accuracy. If the root-mean-square speed of the gas mo
> We have two equal-size boxes, A and B. Each box contains gas that behaves as an ideal gas. We insert a thermometer into each box and find that the gas in box A is at 50 0C while the gas in box B is at 10 0C. This is all we know about the gas in the boxes
> (a) What is the total translational kinetic energy of the air in an empty room that has dimensions 8.00 m × 12.00 m × 4.00 m if the air is treated as an ideal gas at 1.00 atm? (b). What is the speed of a 2000-kg automobile if its kinetic energy equals t
> Consider an ideal gas at 270 C and 1.00 atm. To get some idea how close these molecules are to each other, on the average, imagine them to be uniformly spaced, with each molecule at the center of a small cube. (a). What is the length of an edge of each
> The Lagoon Nebula (Fig. E18.24) is a cloud of hydrogen gas located 3900 light-years from the earth. The cloud is about 45 light-years in diameter and glows because of its high temperature of 7500 K. (The gas is raised to this temperature by the stars tha
> Modern vacuum pumps make it easy to attain pressures of the order of 10-13 atm in the laboratory. Consider a volume of air and treat the air as an ideal gas. (a). At a pressure of 9.00 × 10-14 atm and an ordinary temperature of 300.0 K, how many molecul
> (a).Calculate the mass of nitrogen present in a volume of 3000 cm3 if the gas is at 22.0°C and the absolute pressure of 2.00 × 10-13 atm is a partial vacuum easily obtained in laboratories. (b).What is the density (in kg/m3) of the N2?
> With the assumptions of Example 18.4 (Section 18.1), at what elevation above sea level is air pressure 90% of the pressure at sea level?
> Three moles of an ideal gas are in a rigid cubical box with sides of length 0.300 m. (a). What is the force that the gas exerts on each of the six sides of the box when the gas temperature is 20.0° C? (b) What is the force when the temperature of the g
> (a). Show that the fractional change in the speed of sound (dv/v) due to a very small temperature change dT is given by dv/v = 1 2 dT/T. (Hint: Start with Eq. 16.10.) Eq. 16.10: U =
> Example 16.1 (Section 16.1) showed that for sound waves in air with frequency 1000 Hz, a displacement amplitude of 1.2 × 10-8 m produces a pressure amplitude of 3.0 × 10-2 Pa. (a). What is the wavelength of these waves? (b). For 1000-Hz waves in air, w
> A sled with mass 12.00 kg moves in a straight line on a frictionless, horizontal surface. At one point in its path, its speed is 4.00 m/s; after it has traveled 2.50 m beyond this point, its speed is 6.00 m/s. Use the work–energy theorem to find the forc
> You throw a 3.00-N rock vertically into the air from ground level. You observe that when it is 15.0 m above the ground, it is traveling at 25.0 m/s upward. Use the work–energy theorem to find (a) the rock’s speed just as it left the ground and (b) its ma
> You are a member of an Alpine Rescue Team. You must project a box of supplies up an incline of constant slope angle a so that it reaches a stranded skier who is a vertical distance h above the bottom of the incline. The incline is slippery, but there is
> Use the work–energy theorem to solve each of these problems. You can use Newton’s laws to check your answers. (a) A skier moving at 5.00 m>s encounters a long, rough horizontal patch of snow having a coefficient of kinetic friction of 0.220 with her skis
> Use the work–energy theorem to solve each of these problems. You can use Newton’s laws to check your answers. Neglect air resistance in all cases. (a) A branch falls from the top of a 95.0-m-tall redwood tree, starting from rest. How fast is it moving wh
> A 4.80-kg watermelon is dropped from rest from the roof of an 18.0-m-tall building and feels no appreciable air resistance. (a) Calculate the work done by gravity on the watermelon during its displacement from the roof to the ground. (b) Just before it s
> Using a cable with a tension of 1350 N, a tow truck pulls a car 5.00 km along a horizontal roadway. (a) How much work does the cable do on the car if it pulls horizontally? If it pulls at 35.0° above the horizontal? (b) How much work does the cable do on
> About 50,000 years ago, a meteor crashed into the earth near present-day Flagstaff, Arizona. Measurements from 2005 estimate that this meteor had a mass of about 1.4 × 108 kg (around 150,000 tons) and hit the ground at a speed of 12 km/s. (a) How much ki
> (a) In the Bohr model of the atom, the ground-state electron in hydrogen has an orbital speed of 2190 km/s. What is its kinetic energy? (Consult Appendix F.) (b) If you drop a 1.0-kg weight (about 2 lb) from a height of 1.0 m, how many joules of kinetic
> Adult cheetahs, the fastest of the great cats, have a mass of about 70 kg and have been clocked to run at up to 72 mi/h 132 m/s2. (a) How many joules of kinetic energy does such a swift cheetah have? (b) By what factor would its kinetic energy change if
> You are holding a briefcase by the handle, with your arm straight down by your side. Does the force your hand exerts do work on the briefcase when (a) you walk at a constant speed down a horizontal hallway and (b) you ride an escalator from the first to
> A 1.50-kg book is sliding along a rough horizontal surface. At point A it is moving at 3.21 m>s, and at point B it has slowed to 1.25 m/s. (a) How much work was done on the book between A and B? (b) If -0.750 J of work is done on the book from B to C, ho
> An airplane in flight is subject to an air resistance force proportional to the square of its speed v. But there is an additional resistive force because the airplane has wings. Air flowing over the wings is pushed down and slightly forward, so from Newt
> We usually ignore the kinetic energy of the moving coils of a spring, but let’s try to get a reasonable approximation to this. Consider a spring of mass M, equilibrium length L0, and force constant k. The work done to stretch or compress the spring by a
> A boxed 10.0-kg computer monitor is dragged by friction 5.50 m upward along a conveyor belt inclined at an angle of 36.9° above the horizontal. If the monitor’s speed is a constant 2.10 cm/s, how much work is done on the monitor by (a) friction, (b) grav
> A 128.0-N carton is pulled up a frictionless baggage ramp inclined at 30.0° above the horizontal by a rope exerting a 72.0-N pull parallel to the ramp’s surface. If the carton travels 5.20 m along the surface of the ramp, calculate the work done on it by
> A 12.0-kg package in a mail-sorting room slides 2.00 m down a chute that is inclined at 53.0° below the horizontal. The coefficient of kinetic friction between the package and the chute’s surface is 0.40. Calculate the work done on the package by (a) fri
> You push your physics book 1.50 m along a horizontal tabletop with a horizontal push of 2.40 N while the opposing force of friction is 0.600 N. How much work does each of the following forces do on the book: (a) your 2.40-N push, (b) the friction force,
> A man pushes on a piano with mass 180 kg; it slides at constant velocity down a ramp that is inclined at 19.0° above the horizontal floor. Neglect any friction acting on the piano. Calculate the magnitude of the force applied by the man if he pushes (a)
> A 1130-kg car is held in place by a light cable on a very smooth (frictionless) ramp (Fig. E5.8). The cable makes an angle of 31.0° above the surface of the ramp, and the ramp itself rises at 25.0° above the horizontal. (a) Draw a f
> Find the tension in each cord in Fig. E5.7 if the weight of the suspended object is w. Fig. E5.7: Figure E5.7 (a) (b) 30° 45° 45° B A B 60° C C
> It is often said that “friction always opposes motion.” Give at least one example in which (a) static friction causes motion, and (b) kinetic friction causes motion.
> A large wrecking ball is held in place by two light steel cables (Fig. E5.6). If the mass m of the wrecking ball is 3620 kg, what are (a) the tension TB in the cable that makes an angle of 40° with the vertical and (b) the tension TA in the ho
> A picture frame hung against a wall is suspended by two wires attached to its upper corners. If the two wires make the same angle with the vertical, what must this angle be if the tension in each wire is equal to 0.75 of the weight of the frame? (Ignore
> In the treatment of spine injuries, it is often necessary to provide tension along the spinal column to stretch the backbone. One device for doing this is the Stryker frame (Fig. E5.4a). A weight W is attached to the patient (sometimes around a neck coll
> A 75.0-kg wrecking ball hangs from a uniform, heavy-duty chain of mass 26.0 kg. (a) Find the maximum and minimum tensions in the chain. (b) What is the tension at a point three-fourths of the way up from the bottom of the chain?
> A 45.0-kg crate of tools rests on a horizontal floor. You exert a gradually increasing horizontal push on it, and the crate just begins to move when your force exceeds 313 N. Then you must reduce your push to 208 N to keep it moving at a steady 25.0 cm/s
> A box of bananas weighing 40.0 N rests on a horizontal surface. The coefficient of static friction between the box and the surface is 0.40, and the coefficient of kinetic friction is 0.20. (a) If no horizontal force is applied to the box and the box is a
> A stockroom worker pushes a box with mass 16.8 kg on a horizontal surface with a constant speed of 3.50 m/s. The coefficient of kinetic friction between the box and the surface is 0.20. (a) What horizontal force must the worker apply to maintain the moti
> In a laboratory experiment on friction, a 135-N block resting on a rough horizontal table is pulled by a horizontal wire. The pull gradually increases until the block begins to move and continues to increase thereafter. Figure E5.26 shows a graph of the
> After emergencies with major blood loss, a patient is placed in the Trendelenburg position, in which the foot of the bed is raised to get maximum blood flow to the brain. If the coefficient of static friction between a typical patient and the bed sheets
> A 5.00-kg crate is suspended from the end of a short vertical rope of negligible mass. An upward force F1t2 is applied to the end of the rope, and the height of the crate above its initial position is given by y(t)=(2.80 m/s)t +(0.610 m/s3)t3. What is th
> You are pushing a large crate from the back of a freight elevator to the front as the elevator is moving to the next floor. In which situation is the force you must apply to move the crate the least, and in which is it the greatest: when the elevator is
> A 2.00-kg box is moving to the right with speed 9.00 m/s on a horizontal, frictionless surface. At t = 0 a horizontal force is applied to the box. The force is directed to the left and has magnitude F(t)=(6.00 N/s2)t2. (a) What distance does the box move
> A 2540-kg test rocket is launched vertically from the launch pad. Its fuel (of negligible mass) provides a thrust force such that its vertical velocity as a function of time is given by v(t)= At + Bt2, where A and B are constants and time is measured fro
> When jumping straight up from a crouched position, an average person can reach a maximum height of about 60 cm. During the jump, the person’s body from the knees up typically rises a distance of around 50 cm. To keep the calculations simple and yet get a
> A 550-N physics student stands on a bathroom scale in an elevator that is supported by a cable. The combined mass of student plus elevator is 850 kg. As the elevator starts moving, the scale reads 450 N. (a) Find the acceleration of the elevator (magnitu
> In Fig. E5.2 each of the suspended blocks has weight w. The pulleys are frictionless, and the ropes have negligible weight. In each case, draw a free-body diagram and calculate the tension T in the rope in terms of w. Fig. E5.2: Figure E5.2 (a) (b)
> A 750.0-kg boulder is raised from a quarry 125 m deep by a long uniform chain having a mass of 575 kg. This chain is of uniform strength, but at any point it can support a maximum tension no greater than 2.50 times its weight without breaking. (a) What i
> A transport plane takes off from a level landing field with two gliders in tow, one behind the other. The mass of each glider is 700 kg, and the total resistance (air drag plus friction with the runway) on each may be assumed constant and equal to 2500 N
> A light rope is attached to a block with mass 4.00 kg that rests on a frictionless, horizontal surface. The horizontal rope passes over a frictionless, massless pulley, and a block with mass m is suspended from the other end. When the blocks are released
> An 8.00-kg block of ice, released from rest at the top of a 1.50-m-long frictionless ramp, slides downhill, reaching a speed of 2.50 m>s at the bottom. (a) What is the angle between the ramp and the horizontal? (b) What would be the speed of the ice at t

