Question: A light is to be placed atop
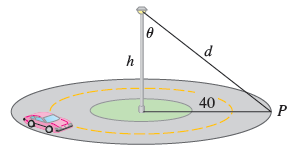
A light is to be placed atop a pole of height h feet to illuminate a busy traffic circle, which has a radius of 40 ft. The intensity of illumination I at any point P on the circle is directly proportional to the cosine of the angle θ (see the figure) and inversely proportional to the square of the distance d from the source.
(a) How tall should the light pole be to maximize I?
(b) Suppose that the light pole is h feet tall and that a woman is walking away from the base of the pole at the rate of 4 ft/s. At what rate is the intensity of the light at the point on her back 4 ft above the ground decreasing when she reaches the outer edge of the traffic circle?
Transcribed Image Text:
d h 40
> Evaluate the indefinite integral. Illustrate and check that your answer is reasonable by graphing both the function and its antiderivative (take C = 0). x3 -dx x² + 1
> The table shows how the average age of first marriage of Japanese women has varied since 1950. (a) Use a graphing calculator or computer to model these data with a fourth-degree polynomial. (b) Use part (a) to find a model for A’(t).
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. 3 dx = 8 -2 X
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. So (x – x) dx represents the area under the curve y = x – x³ from 0 to 2.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f is continuous on [a, b], then d f(x) dx ) -f(x) dx
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If fo f(x) dx = 0, then f(x) = 0 for 0 <x< 1.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. fe*ax = {f e*dx + f, e* dx ex* dx J5 Jo
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. All continuous functions have antiderivatives.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. All continuous functions have derivatives.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. L (ax? + bx + c) dx = 2 (ax? + c) dx
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. sin x – 6xº + dx = 0 - (1 + x*)?
> Evaluate the indefinite integral. Illustrate and check that your answer is reasonable by graphing both the function and its antiderivative (take C = 0). cs X dx V1 + sin x
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f and g are differentiable and f(x) > g(x) for a <x < b, then f'(x) > g'(x) for a <x < b.
> The table gives the population of the world P(t), in millions, where t is measured in years and t = 0 corresponds to the year 1900. (a) Estimate the rate of population growth in 1920 and in 1980 by averaging the slopes of two secant lines. (b) Use a g
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f and g are continuous and f(x) > g(x) for a < x< b, then g(x) dx
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f' is continuous on [1, 3], then f'(v) dv = f(3) – f(1).
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f is continuous on [a, b] and f(x) > 0, then L VF) dx f(x) dx
> Use the given graph of f to find the Riemann sum with six subintervals. Take the sample points to be (a) left endpoints and (b) midpoints. In each case draw a diagram and explain what the Riemann sum represents. y = f(x) 2- 6. 2.
> Boyle’s Law states that when a sample of gas is compressed at a constant temperature, the product of the pressure and the volume remains constant: PV = C. (a) Find the rate of change of volume with respect to pressure. (b) A sample of gas is in a contain
> Estimate the value of the number c such that the area under the curve y = sinh cx between x = 0 and x = 1 is equal to 1.
> A population of honeybees increased at a rate of r(t) bees per week, where the graph of r is as shown. Use the Midpoint Rule with six subintervals to estimate the increase in the bee population during the first 24 weeks. 12000 8000 4000 4 8 12 16 20
> In Example 6 we considered a bacteria population that doubles every hour. Suppose that another population of bacteria triples every hour and starts with 400 bacteria. Find an expression for the number n of bacteria after t hours and use it to estimate th
> A radar gun was used to record the speed of a runner at the times given in the table. Use the Midpoint Rule to estimate the distance the runner covered during those 5 seconds. 1 (s) v (m/s) I (s) v (m/s) 3.0 10.51 0.5 4.67 3.5 10.67 1.0 7.34 4.0 10.
> A particle moves along a line with velocity function v(t) = t2 - t, where v is measured in meters per second. Find (a) the displacement and (b) the distance traveled by the particle during the time interval [0, 5].
> Find the vector that has the same direction as 6, 2, −3 but has length 4.
> Find a unit vector that has the same direction as the given vector. 8i - j + 4k
> Find a + b, 4a + 2b, |a |, and |a - b |. a = 8, 1, −4 , b = 5, −2, 1
> Find a + b, 4a + 2b, |a |, and |a - b |. a = 4i - 3j + 2k, b = 2i - 4k
> Use vectors to prove that the line joining the midpoints of two sides of a triangle is parallel to the third side and half its length.
> The cost function for a certain commodity is C(q) = 84 + 0.16q - 0.0006q2 + 0.000003q3 (a) Find and interpret C9s100d. (b) Compare C’(100) with the cost of producing the 101st item.
> Prove Property 5 of vectors algebraically for the case n = 3. Then use similar triangles to give a geometric proof.
> Figure 16 gives a geometric demonstration of Property 2 of vectors. Use components to give an algebraic proof of this fact for the case n = 2.
> Find a + b, 4a + 2b, |a |, and |a - b |. a = 5i + 3j, b = -i - 2j
> What is the relationship between the point (4, 7) and the vector (4, 7)? Illustrate with a sketch.
> Find a + b, 4a + 2b, |a |, and |a - b |. a = −3, 4 , b = 9, −1
> Find an equation of the set of all points equidistant from the points A (-1, 5, 3) and B (6, 2, -2). Describe the set.
> Consider the points P such that the distance from P to A (-1, 5, 3d is twice the distance from P to B (6, 2, -2). Show that the set of all such points is a sphere, and find its center and radius.
> If A, B, and C are the vertices of a triangle, find АВ + ВС + СА
> Write inequalities to describe the region. The region consisting of all points between (but not on) the spheres of radius r and R centered at the origin, where r < R
> Differentiate. f (t) = cot t / et
> Find the sum of the given vectors and illustrate geometrically. 3, −1 , −1, 5
> Write inequalities to describe the region. The region between the yz-plane and the vertical plane x = 5
> Describe in words the region of R3 represented by the equation(s) or inequality. x2 + y2 + z2 > 2z
> Find the sum of the given vectors and illustrate geometrically. −1, 4 , 6, −2
> Find dy/dx by implicit differentiation. x2 / x + y = y2 + 1
> Find the local and absolute extreme values of the function on the given interval. f (x) = x3 - 9x2 + 24x - 2, [0, 5]
> Newton’s Law of Gravitation says that the magnitude F of the force exerted by a body of mass m on a body of mass M is F = GmM / r2 where G is the gravitational constant and r is the distance between the bodies. (a) Find dF/dr and explain its meaning. Wha
> Use the guidelines of Section 4.5 to sketch the curve. y = 3x4 - 4x3 + 2
> Water is flowing at a constant rate into a spherical tank. Let V(t) be the volume of water in the tank and H(t) be the height of the water in the tank at time t. (a) What are the meanings of V’(t) and H’(t)? Are these derivatives positive, negative, or z
> Show that, for x > 0, x/1 + x2 < tan-1x < x
> A rectangular beam will be cut from a cylindrical log of radius 10 inches. (a) Show that the beam of maximal cross-sectional area is a square. (b) Four rectangular planks will be cut from the four sections of the log that remain after cutting the square
> In an automobile race along a straight road, car A passed car B twice. Prove that at some time during the race their accelerations were equal. State the assumptions that you make.
> A canister is dropped from a helicopter 500 m above the ground. Its parachute does not open, but the canister has been designed to withstand an impact velocity of 100 m/s. Will it burst?
> Use the guidelines of Section 4.5 to sketch the curve. y = -2x3 - 3x2 + 12x + 5
> The quantity of charge Q in coulombs (C) that has passed through a point in a wire up to time t (measured in seconds) is given by Q(t) = t3 - 2t2 + 6t + 2. Find the current when (a) t = 0.5 s and (b) t = 1 s. [See Example 3. The unit of current is an amp
> Investigate the family of curves given by f (x) = x4 + x3 + cx2 In particular you should determine the transitional value of c at which the number of critical numbers changes and the transitional value at which the number of inflection points changes. Il
> (a) If f (x) = 0.1ex + sin x, -4 ≤ x ≤ 4, use a graph of f to sketch a rough graph of the antiderivative F of f that satisfies F(0) = 0. (b) Find an expression for F(x). (c) Graph F using the expression in part (b). Compare with your sketch in part (a).
> A particle is moving with the given data. Find the position of the particle. a(t) = sin t + 3 cos t, s(0) = 0, v(0) = 2
> A particle is moving with the given data. Find the position of the particle. v(t) = 2t – 1/(1 + t2), s(0) = 1
> Find f. f ‘(t) = 2t - 3 sin t, f (0) = 5
> Use the guidelines of Section 4.5 to sketch the curve. y = 2 - 2x - x3
> Use the guidelines in Section 4.5 to sketch the curve y = x sin x, 0 ≤ x ≤ 2 π. Use Newton’s method when necessary.
> Use Newton’s method to find the absolute maximum value of the function f (t) = cos t + t - t2 correct to eight decimal places.
> Use Newton’s method to find all solutions of the equation sin x = x2 - 3x + 1 correct to six decimal places.
> Use Newton’s method to find the root of the equation x5 - x4 + 3x2 - 3x - 2 = 0 in the interval [1, 2] correct to six decimal places.
> A manufacturer determines that the cost of making x units of a commodity is C(x) = 1800 + 25x - 0.2x2 + 0.001x3 and the demand function is p(x) = 48.2 - 0.03x. (a) Graph the cost and revenue functions and use the graphs to estimate the production level f
> A hockey team plays in an arena with a seating capacity of 15,000 spectators. With the ticket price set at $12, average attendance at a game has been 11,000. A market survey indicates that for each dollar the ticket price is lowered, average attendance w
> The figure shows the graph of the derivative f ‘ of a function f. (a) On what intervals is f increasing or decreasing? (b) For what values of x does f have a local maximum or minimum? (c) Sketch the graph of f ’â
> A metal storage tank with volume V is to be constructed in the shape of a right circular cylinder surmounted by a A metal storage tank with volume V is to be constructed in the shape of a right circular cylinder surmounted by a
> The mass of the part of a metal rod that lies between its left end and a point x meters to the right is 3x2 kg. Find the linear density (see Example 2) when x is (a) 1 m, (b) 2 m, and (c) 3 m. Where is the density the highest? The lowest?
> Solve Exercise 55 when |CD| = 2 cm. Exercise 55: In ΔABC, D lies on AB, CD AB, |AD| = |BD| = 4 cm, and |CD| = 5 cm. Where should a point P be chosen on CD so that the sum |PA | + |PB | + |PC | is a minimum?
> In ΔABC, D lies on AB, CD AB, |AD| = |BD| = 4 cm, and |CD| = 5 cm. Where should a point P be chosen on CD so that the sum |PA | + |PB | + |PC | is a minimum?
> Find the volume of the largest circular cone that can be inscribed in a sphere of radius r.
> Find the smallest possible area of an isosceles triangle that is circumscribed about a circle of radius r.
> Find the point on the hyperbola xy = 8 that is closest to the point (3, 0).
> Find two positive integers such that the sum of the first number and four times the second number is 1000 and the product of the numbers is as large as possible.
> Sketch the graph of a function that satisfies the given conditions. f is odd, f ‘(x) f'(x) > 0 for x > 2, f"(x) > 0 for 0 < x< 3, f"(x) < 0 for x > 3, lim f(x) = -2 X 00
> Let g(x) = f (x2), where f is twice differentiable for all x, f ‘(x) > 0 for all x ≠ 0, and f is concave downward on (-∞, 0) and concave upward on (0, ∞). (a) At what numbers does g have an extreme value? (b) Discuss the concavity of g.
> For what values of the constants a and b is (1, 3) a point of inflection of the curve y = ax3 + bx2?
> By applying the Mean Value Theorem to the function f (x) = x1/5 on the interval [32, 33], show that 2 < 5 33 < 2.0125
> (a) The volume of a growing spherical cell is V = 4/3 πr3, where the radius r is measured in micrometers (1 μm − 1026 m). Find the average rate of change of V with respect to r when r changes from (i) 5 to 8 μm (ii) 5 to 6 μm (iii) 5 to 5.1 μm (b) Find t
> Suppose that f is continuous on [0, 4], f (0) = 1, and 2 ≤ f ‘(x) ≤ 5 for all x in (0, 4). Show that 9 ≤ f (4) ≤ 21.
> Show that the equation 3x + 2 cos x + 5 = 0 has exactly one real root.
> Investigate the family of functions f (x) = ln(sin x + C). What features do the members of this family have in common? How do they differ? For which values of C is f continuous on (-∞, ∞)? For which values of C does f have no graph at all? What happens a
> (a) Find the average rate of change of the area of a circle with respect to its radius r as r changes from (i) 2 to 3 (ii) 2 to 2.5 (iii) 2 to 2.1 (b) Find the instantaneous rate of change when r = 2. (c) Show that the rate of change of the area of a cir
> (a) Graph the function f (x) = 1/(1 + e1/x). (b) Explain the shape of the graph by computing the limits of f (x) as x approaches ∞, -∞, 0+, and 0-. (c) Use the graph of f to estimate the coordinates of the inflection points. (d) Use your CAS to compute a
> Produce graphs of f that reveal all the important aspects of the curve. Use graphs of f ‘ and f ’’ to estimate the intervals of increase and decrease, extreme values, intervals of concavity, and inflection points. In Exercise 35 use calculus to find thes
> Produce graphs of f that reveal all the important aspects of the curve. Use graphs of f ‘ and f ’’ to estimate the intervals of increase and decrease, extreme values, intervals of concavity, and inflection points. In Exercise 35 use calculus to find thes
> A spherical balloon is being inflated. Find the rate of increase of the surface area (S = 4πr2) with respect to the radius r when r is (a) 1 ft, (b) 2 ft, and (c) 3 ft. What conclusion can you make?
> Use the guidelines of Section 4.5 to sketch the curve. y = x + ln(x2 + 1)
> Use the guidelines of Section 4.5 to sketch the curve. y = (x – 2)e-x
> Sketch the graph of a function that satisfies the given conditions. f (0) = 0, f is continuous and even, f ‘(x) = 2x if 0 < x < 1, f ‘(x) = -1 if 1 < x < 3, f ‘(x) = 1 if x > 3
> Use the guidelines of Section 4.5 to sketch the curve. y = sin-1(1/x)
> Use the guidelines of Section 4.5 to sketch the curve. y = 4x - tan x, -π/2 < x
> Use the guidelines of Section 4.5 to sketch the curve. y = ex sin x, -π ≤ x ≤ π
> A stone is dropped into a lake, creating a circular ripple that travels outward at a speed of 60 cm/s. Find the rate at which the area within the circle is increasing after (a) 1 s, (b) 3 s, and (c) 5 s. What can you conclude?
> Some of the highest tides in the world occur in the Bay of Fundy on the Atlantic Coast of Canada. At Hopewell Cape the water depth at low tide is about 2.0 m and at high tide it is about 12.0 m. The natural period of oscillation is a little more than 12
> Differentiate. y = c cos t + t2 sin t
> (a) Sodium chlorate crystals are easy to grow in the shape of cubes by allowing a solution of water and sodium chlorate to evaporate slowly. If V is the volume of such a cube with side length x, calculate dV / dx when x = 3 mm and explain its meaning. (b
> Find the local and absolute extreme values of the function on the given interval. f (x) = x2e-x, [-1, 3]

