[SOLVED] A population of honeybees increased at a

A population of honeybees increased at a rate of r (t) bees per week, where the graph of is as shown. Use Simpsonâ€™s Rule with six subintervals to estimate the increase in the bee population during the first 24 weeks.

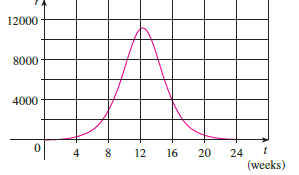
Transcribed Image Text:

12000 8000 4000 8 8 12 16 20 4 24 (weeks)

Related Questions

> For what value of a is the following equation true? + a = e lim x - a х —

> A string is wound around a circle and then unwound while being held taut. The curve traced by the point P at the end of the string is called the involute of the circle. If the circle has radius r and center O and the initial position of is P (r, 0), and

> If f (x) = fg(x)01/√1 + t3, dt, where g (x) = fcosx0[1 + sin (t2)], dt, find f'(π/2).

> Find the approximations Ln, Rn, Tn and Mn for n = 5, 10 and 20. Then compute the corresponding errors EL, ER and ET. and EM (Round your answers to six decimal places. You may wish to use the sum command on a computer algebra system.) What observations ca

> A solid is generated by rotating about the -axis the region under the curve y = f (x), where f is a positive function and x > 0. The volume generated by the part of the curve from x = 0 to x = b is b2 for all b > 0. Find the function f.

> In lies on ∆ABC, D, lies on AB, |CD| = 5cm, |AD| = 4 cm, |BD = 4cm, and CD ⊥ AB. Where should a point p be chosen on CD so that the sum |PA| + |PB| + |PC| is a minimum? What if |CD| = 2 cm?

> Find the volume of the largest circular cone that can be inscribed in a sphere of radius r.

> (a). Use an improper integral and information from Exercise 27 to find the work needed to propel a 1000-kg satellite out of the earthâs gravitational field. Exercise 27: (a). Newtonâs Law of Gravitation states that t

> Find the smallest possible area of an isosceles triangle that is circumscribed about a circle of radius r.

> Find the point on the hyperbola xy = 8 that is closest to the point (3, 0).

> A water skier skis over the ramp shown in the figure at a speed of 30 ft/s. How fast is she rising as she leaves the ramp? -15 ft

> A balloon is rising at a constant speed of 5 ft/s. A boy is cycling along a straight road at a speed of 15 ft/s. When he passes under the balloon, it is 45 ft above him. How fast is the distance between the boy and the balloon increasing 3 s later?

> A paper cup has the shape of a cone with height 10 cm and radius 3 cm (at the top). If water is poured into the cup at a rate of 2 cm3/s, how fast is the water level rising when the water is 5 cm deep?

> The angle of elevation of the sun is decreasing at a rate of 0.25 rad/h. How fast is the shadow cast by a 400-ft-tall building increasing when the angle of elevation of the sun is π/6?

> Evaluate the limit. lim x→(π/2)- (tan x) cos x

> The left, right, Trapezoidal, and Midpoint Rule approximations were used to estimate f20 f (x) dx, where f is the function whose graph is shown. The estimates were 0.7811, 0.8675, 0.8632, and 0.9540, and the same number of subintervals were used in each

> Evaluate the limit. lim x→1+ (x / 1 – x – 1/ ln x)

> Find the volumes of the solids obtained by rotating the region bounded by the curves y = x and y = x2 about the following lines. (a). The x-axis (b). The y-axis (c). y = 2

> Evaluate the integral. f-55 e dx

> A 1600-lb elevator is suspended by a 200-ft cable that weighs 10 lb/ft. How much work is required to raise the elevator from the basement to the third floor, a distance of 30 ft?

> Evaluate the limit. lim x→0+ x2 ln x

> Evaluate the limit. lim x→∞ x3 e-x

> Evaluate the limit. lim x→∞ e4x -1 – 4x/x2

> Find the local and absolute extreme values of the function on the given interval. Зх — 4 f(x) [-2, 2] x² + 1'

> Evaluate the limit. lim x→0 e4x – 1 – 4x /x2

> Evaluate the limit. lim x→0 1 – cos x / x2 + x

> Evaluate the limit. lim x→0 tan πx/ln (1 + x)

> For what values of the constants a and b is a point of inflection of the curve y = x3 + ax2 + bx + 1?

> If a diver of mass m stands at the end of a diving board with length L and linear density p, then the board takes on the shape of a curve y = f (x), where E and are positive constants that depend on the material of the board and g ( (a). Find an expre

> Evaluate the integral. f-10 (2x – ex) dx

> Find the local and absolute extreme values of the function on the given interval. f(x) = x/T- x, [-1, 1]

> Let R be the region in the first quadrant bounded by the curves y = x3 and y = 2x – x2. Calculate the following quantities. (a). The area of R (b). The volume obtained by rotating R about the x-axis (c). The volume obtained by rotating R about the y-axis

> Graph f (x) = e-1/x2 in a viewing rectangle that shows all the main aspects of this function. Estimate the inflection points. Then use calculus to find them exactly.

> (a). Find the vertical and horizontal asymptotes, if any. (b). Find the intervals of increase or decrease. (c). Find the local maximum and minimum values. (d). Find the intervals of concavity and the inflection points. (e). Use the information from parts

> The figure shows two regions in the first quadrant: A (t) is the area under the curve y = sin (x2) from 0 to t, and B (t) is the area of the triangle with vertices O, P, and (t, 0). Find limtâ0+A (t)/B (t). y y. P(t, sin(12)) P(t,

> If f' is continuous on [0, ∞] and limx→∞f (x) = 0, show that f∞0f' (x) dx = -f (0).

> If oil leaks from a tank at a rate r (t) of gallons per minute at time f020 r (t) dt, what does represent?

> Evaluate the integral. f18 3√x dx

> If n is a positive integer, prove that f10 (ln x) n dx = (-1) n n!

> If f' is continuous on [a, b], show that 2 fba f (x) f' (x) dx = [f (b)]2 – [f (a)]2

> Find a function f and a value of the constant a such that 2 f(t) dt = 2 sin x – 1

> Let be the region bounded by the curves y = tan (x2), x = 1 and y = 0. Use the Midpoint Rule with n = 4 to estimate the following quantities. (a). The area of (b). The volume obtained by rotating about the -axis

> If f is a continuous function such that for all x, find an explicit formula for f (x). , r) dt = xe² + [ e "f)di

> Find the local and absolute extreme values of the function on the given interval. f(x) = x' – 6x² + 9x + 1, [2, 4]

> Suppose that the temperature in a long, thin rod placed along the x-axis is initially C/(2a) if |x| a. It can be shown that if the heat diffusivity of the rod is k, then the temperature of the rod at the point x at time t is To find the temperature d

> Let r (t) be the rate at which the world’s oil is consumed, where is measured in years starting at t = 0 on January 1, 2000, and r (t) is measured in barrels per year. What does f80r (t) dt represent?

> The speedometer reading (v) on a car was observed at 1-minute intervals and recorded in the chart. Use Simpsonâs Rule to estimate the distance traveled by the car. t (min) v (mi/h) t (min) v (mi/h) 40 6 56 1 42 7 57 2 45 8 57 3 49

> Evaluate the integral. f01 x4/5 dx

> (a). Evaluate the integral f∞0 xne-x dx for n = 0, 1, 2, and 3. (b). Guess the value of f∞0 xne-x dx when n is an arbitrary positive integer. (c). Prove your guess using mathematical induction.

> A particle moves along a line with velocity function v (t) = t2 - t, where is measured in meters per second. Find (a) the displacement and (b) the distance traveled by the particle during the time interval [0, 5].

> For what values of a is f∞0eax cos x dx convergent? Use the Table of Integrals to evaluate the integral for those values of a.

> Use the Comparison Theorem to determine whether the Integral is convergent or divergent. dx x' + 2

> Evaluate the integral or show that it is divergent. f62y/√y – 2, dy

> Find the volume of the solid obtained by rotating about the x-axis the region bounded by the curves y = e-2x, y = 1 + x and x = 1.

> Evaluate the integral or show that it is divergent. fe1dx/x √lnx

> Evaluate the integral or show that it is divergent. f101/2 – 3x, dx

> Evaluate the integral or show that it is divergent. f0-∞e-2x dx

> Evaluate the integral or show that it is divergent. f∞0ln x/x4, dx

> Use a graph to give a rough estimate of the area of the region that lies beneath the given curve. Then find the exact area. y = sin x, 0 <I<T

> Evaluate the integral or show that it is divergent. f∞11/ (2x + 1)3, dx

> Use Newton’s method to find the coordinates, correct to six decimal places, of the point on the parabola y = (x – 1)2 that is closest to the origin.

> Use the properties of integrals to verify that 0 < f10x4 cos x dx < 0.2.

> Use Property 8 of integrals to estimate the value of f31√x2 + 3, dx.

> Find the most general antiderivative of the function. g(1) = (1 + t)//E

> Find the most general antiderivative of the function. f(x) = e* – (2//x)

> Use Simpson’s Rule with n = 6 to estimate the area under the curve y = ex/x from x = 1 to x = 4.

> The curve traced out by a point at a distance 1 m from the center of a circle of radius 2 m as the circle rolls along the x-axis is called a trochoid and has parametric equations One arch of the trochoid is given by the parameter interval 0 x= 20 -

> Use Newton’s method to find the absolute maximum value of the function f (t) = cos t + t – t2 correct to eight decimal places.

> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpsonâs Rule with n = 10 to approximate the given integral. Round your answers to six decimal places. Can you say whether your answers are underestimates or overestimates?

> What is wrong with the equation? f0π sec2x dx = tan x]0π = 0

> Use the Table of Integrals on the Reference Pages to evaluate the integral. cot x dx V1 + 2 sin x

> A stone was dropped off a cliff and hit the ground with a speed of 120 ft/s. What is the height of the cliff?

> Use the Table of Integrals on the Reference Pages to evaluate the integral. x² + x + 1 dx

> Use the Table of Integrals on the Reference Pages to evaluate the integral. | csc*t dt

> Use the Table of Integrals on the Reference Pages to evaluate the integral. VT- e2* dx

> Find the derivative of the function. y = f3x+12x sin (t4) dt

> Find the derivative of the function. y = fx√x, et/t, dt

> Find the derivative of the function. g (x) = fsinx11 – t2/1 + t4 dt

> Find the area of the region bounded by the given curves. x + y = 0, x= y² + 3y

> What is wrong with the equation? f-13 1/x2 dx = x-1/-1]-13 = -4/3

> The length of time spent waiting in line at a certain bank is modeled by an exponential density function with mean 8 minutes. (a). What is the probability that a customer is served in the first 3 minutes? (b). What is the probability that a customer has

> Lengths of human pregnancies are normally distributed with mean 268 days and standard deviation 15 days. What percentage of pregnancies last between 250 days and 280 days?

> (a). Explain why the function is a probability density function. (b). Find P (X (c). Calculate the mean. Is the value what you would expect? sin f(x) = { 20 10 if 0 <x< 10 if x<0 or x> 10

> (a). Use Newton’s method with x1 = 1 to find the root of the equation x3 – x = 1 correct to six decimal places. (b). Solve the equation in part (a) using x1 = 0.6 as the initial approximation. (c). Solve the equation in part (a) using x1 = 0.57. (You def

> After a 6-mg injection of dye into a heart, the readings of dye concentration at two-second intervals are as shown in the table. Use Simpsonâs Rule to estimate the cardiac output. c(t) c(t) t 14 4.7 1.9 16 3.3 4 3.3 18 2.1 5.1 20 1

> If f is a continuous function, what is the limit as f→0 of the average value of f on the interval [x, x + h]?

> Find the average value of the function f (x) = x2 √1 + x3 on the interval [0, 2].

> The demand function for a commodity is given by p = 200 – 0.1x – 0.01x2 Find the consumer surplus when the sales level is 100.

> Find the centroid of the region shown. yA (3, 2)

> A gate in an irrigation canal is constructed in the form of a trapezoid 3 ft wide at the bottom, 5 ft wide at the top, and 2 ft high. It is placed vertically in the canal so that the water just covers the gate. Find the hydrostatic force on one side of t

> Evaluate the integral. f03π/2 |sin x| dx

> A trough is filled with water and its vertical ends have the shape of the parabolic region in the figure. Find the hydrostatic force on one end of the trough. 8 ft 4 ft

> Find the area of the region bounded by the given curves. y = 1 - 2x², y = |x|

> Evaluate the integral. f dt/t2 + 6t+ 8

> Evaluate the integral. f sin x cos (cos x) dx

> For what values of m do the line y = mx and the curve y = x/ (x2 + 1) enclose a region? Find the area of the region.

Question: A population of honeybees increased at a

Transcribed Image Text: