Question: A proton with mass m moves in
A proton with mass m moves in one dimension. The potential-energy function is U(x)=(a/x2)-(b/x), where a and b are positive constants. The proton is released from rest at x0 = a/b.
(a) Show that U(x) can be written as
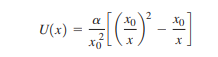
Graph U(x). Calculate U(x0) and thereby locate the point x0 on the graph.
(b) Calculate v(x), the speed of the proton as a function of position. Graph v(x) and give a qualitative description of the motion.
(c) For what value of x is the speed of the proton a maximum? What is the value of that maximum speed?
(d) What is the force on the proton at the point in part (c)?
(e) Let the proton be released instead at x1 = 3a/b. Locate the point x1 on the graph of U(x). Calculate v(x) and give a qualitative description of the motion.
(f) For each release point 1x = x0 and x = x12, what are the maximum and minimum values of x reached during the motion?
Transcribed Image Text:
U(x) = 2
> (a) For the elevator of Example 7.9 (Section 7.2), what is the speed of the elevator after it has moved downward 1.00 m from point 1 in Fig. 7.17? (b) When the elevator is 1.00 m below point 1 in Fig. 7.17, what is its acceleration?
> The food calorie, equal to 4186 J, is a measure of how much energy is released when the body metabolizes food. A certain fruitandcereal bar contains 140 food calories. (a) If a 65kg hiker eats one bar, how high a mountain must he climb to “work off” t
> You are designing a flywheel to store kinetic energy. If all of the following uniform objects have the same mass and same angular velocity, which one will store the greatest amount of kinetic energy? Which will store the least? Explain. (a) A solid spher
> What is the purpose of the spin cycle of a washing machine? Explain in terms of acceleration components.
> A flywheel rotates with constant angular velocity. Does a point on its rim have a tangential acceleration? A radial acceleration? Are these accelerations constant in magnitude? In direction? In each case give your reasoning.
> What is the difference between tangential and radial acceleration for a point on a rotating body?
> Estimate your own moment of inertia about a vertical axis through the center of the top of your head when you are standing up straight with your arms outstretched. Make reasonable approximations and measure or estimate necessary quantities.
> A wheel is rotating about an axis perpendicular to the plane of the wheel and passing through the center of the wheel. The angular speed of the wheel is increasing at a constant rate. Point A is on the rim of the wheel and point B is midway between the r
> A diatomic molecule can be modeled as two point masses, m1 and m2, slightly separated (Fig. Q9.2). If the molecule is oriented along the y-axis, it has kinetic energy K when it spins about the x-axis. What will its kinetic energy (in terms of K) be if it
> You can use any angular measure—radians, degrees, or revolutions—in some of the equations in Chapter 9, but you can use only radian measure in others. Identify those for which using radians is necessary and those for which it is not, and in each case giv
> An elaborate pulley consists of four identical balls at the ends of spokes extending out from a rotating drum (Fig. Q9.18). A box is connected to a light, thin rope wound around the rim of the drum. When it is released from rest, the box acquires a speed
> Two identical balls, A and B, are each attached to very light string, and each string is wrapped around the rim of a frictionless pulley of mass M. The only difference is that the pulley for ball A is a solid disk, while the one for ball B is a hollow di
> A spring of negligible mass has force constant k = 1600 N/m. (a) How far must the spring be compressed for 3.20 J of potential energy to be stored in it? (b) You place the spring vertically with one end on the floor. You then drop a 1.20-kg book onto it
> For the equations for I given in parts (a) and (b) of Table 9.2 to be valid, must the rod have a circular cross section? Is there any restriction on the size of the cross section for these equations to apply? Explain. Table 9.2: TABLE 9.2 Moments o
> Describe how you could use part (b) of Table 9.2 to derive the result in part (d). Table 9.2: TABLE 9.2 Moments of Inertia of Various Bodies (a) Slender rod, axis through center (b) Slender rod, axis through one end (c) Rectangular plate, axis thro
> How might you determine experimentally the moment of inertia of an irregularly shaped body about a given axis?
> In a completely inelastic collision between two objects, where the objects stick together after the collision, is it possible for the final kinetic energy of the system to be zero? If so, give an example in which this would occur. If the final kinetic en
> (a) If the momentum of a single point object is equal to zero, must the object’s kinetic energy also be zero? (b) If the momentum of a pair of point objects is equal to zero, must the kinetic energy of those objects also be zero? (c) If the kinetic energ
> When rain falls from the sky, what happens to its momentum as it hits the ground? Is your answer also valid for Newton’s famous apple?
> When an object breaks into two pieces (explosion, radioactive decay, recoil, etc.), the lighter fragment gets more kinetic energy than the heavier one. This is a consequence of momentum conservation, but can you also explain it by using Newton’s laws of
> At the highest point in its parabolic trajectory, a shell explodes into two fragments. Is it possible for both fragments to fall straight down after the explosion? Why or why not?
> Suppose you catch a baseball and then someone invites you to catch a bowling ball with either the same momentum or the same kinetic energy as the baseball. Which would you choose? Explain.
> A very heavy SUV collides head-on with a very light compact car. Which of these statements about the collision are correct? (a) The amount of kinetic energy lost by the SUV is equal to the amount of kinetic energy gained by the compact; (b) the amount of
> A 1.20-kg piece of cheese is placed on a vertical spring of negligible mass and force constant k = 1800 N/m that is compressed 15.0 cm. When the spring is released, how high does the cheese rise from this initial position? (The cheese and the spring are
> Two objects of mass M and 5M are at rest on a horizontal, frictionless table with a compressed spring of negligible mass between them. When the spring is released, which of the following statements are true? (a) The two objects receive equal magnitudes o
> Two pieces of clay collide and stick together. During the collision, which of these statements are true? (a) Only the momentum of the clay is conserved; (b) only the mechanical energy of the clay is conserved; (c) both the momentum and the mechanical ene
> An apple falls from a tree and feels no air resistance. As it is falling, which of these statements about it are true? (a) Only its momentum is conserved; (b) only its mechanical energy is conserved; (c) both its momentum and its mechanical energy are co
> The net force on a particle of mass m has the potential­ energy function graphed in Fig. 7.24a. If the total energy is E1, graph the speed v of the particle versus its position x. At what value of x is the speed greatest? Sketch v versus x if
> A particle is in neutral equilibrium if the net force on it is zero and remains zero if the particle is displaced slightly in any direction. Sketch the potential energy function near a point of neutral equilibrium for the case of one dimensional moti
> Explain why the points x = A and x = -A in Fig. 7.23b are called turning points. How are the values of E and U related at a turning point? Fig. 7.23b: (b) On the graph, the limits of motion are the points where the U curve intersects the horizontal
> An egg is released from rest from the roof of a building and falls to the ground. As the egg falls, what happens to the momentum of the system of the egg plus the earth?
> A tennis player hits a tennis ball with a racket. Consider the system made up of the ball and the racket. Is the total momentum of the system the same just before and just after the hit? Is the total momentum just after the hit the same as 2 s later, whe
> Figure 7.22a shows the potential ­ energy function for the force Fx = -kx. Sketch the potential ­ energy function for the force Fx = +kx. For this force, is x = 0 a point of equilibrium? Is this equilibrium stable or unstable? Expla
> Since only changes in potential energy are important in any problem, a student decides to let the elastic potential energy of a spring be zero when the spring is stretched a distance x1. The student decides, therefore, to let U = 1 2 k(x - x1)2. Is this
> A spring of negligible mass has force constant k = 800 N/m. (a) How far must the spring be compressed for 1.20 J of potential energy to be stored in it? (b) You place the spring vertically with one end on the floor. You then lay a 1.60-kg book on top of
> In each of Examples 8.10, 8.11, and 8.12 (Section 8.4), verify that the relative velocity vector of the two bodies has the same magnitude before and after the collision. In each case, what happens to the direction of the relative velocity vector? Exampl
> A box slides down a ramp and work is done on the box by the forces of gravity and friction. Can the work of each of these forces be expressed in terms of the change in a potential energy function? For each force explain why or why not.
> In Fig. 8.23b, the kinetic energy of the Ping-Pong ball is larger after its interaction with the bowling ball than before. From where does the extra energy come? Describe the event in terms of conservation of energy. Fig. 8.23b: (b) Moving bowling
> Two objects with different masses are launched vertically into the air by placing them on identical compressed springs and then releasing the springs. The two springs are compressed by the same amount before launching. Ignore air resistance and the masse
> A 1.0kg stone and a 10.0kg stone are released from rest at the same height above the ground. Ignore air resistance. Which of these statements about the stones are true? Justify each answer. (a) Both have the same initial gravitational potential energy.
> (a) A block of wood is pushed against a spring, which is compressed 0.080 m. Does the force on the block exerted by the spring do positive or negative work? Does the potential energy stored in the spring increase or decrease? (b) A block of wood is place
> (a) A book is lifted upward a vertical distance of 0.800 m. During this displacement, does the gravitational force acting on the book do positive work or negative work? Does the gravitational potential energy of the book increase or decrease? (b) A can o
> In Example 8.7 (Section 8.3), where the two gliders of Fig. 8.18 stick together after the collision, the collision is inelastic because K2 < K1 . In Example 8.5 (Section 8.2), is the collision inelastic? Explain. Example 8.7: We repeat the collision de
> A woman holding a large rock stands on a frictionless, horizontal sheet of ice. She throws the rock with speed v0 at an angle a above the horizontal. Consider the system consisting of the woman plus the rock. Is the momentum of the system conserved? Why
> Is it possible for a friction force to increase the mechanical energy of a system? If so, give examples.
> A slingshot will shoot a 10-g pebble 22.0 m straight up. (a) How much potential energy is stored in the slingshot’s rubber band? (b) With the same potential energy stored in the rubber band, how high can the slingshot shoot a 25-g pebble? (c) What physic
> A physics teacher had a bowling ball suspended from a very long rope attached to the high ceiling of a large lecture hall. To illustrate his faith in conservation of energy, he would back up to one side of the stage, pull the ball far to one side until t
> An egg is released from rest from the roof of a building and falls to the ground. Its fall is observed by a student on the roof of the building, who uses coordinates with origin at the roof, and by a student on the ground, who uses coordinates with origi
> An object is released from rest at the top of a ramp. If the ramp is frictionless, does the object’s speed at the bottom of the ramp depend on the shape of the ramp or just on its height? Explain. What if the ramp is not frictionless?
> Use the methods of Challenge Problem 8.104 to calculate the x- and y-coordinates of the center of mass of a semicircular metal plate with uniform density r and thickness t. Let the radius of the plate be a. The mass of the plate is thus M = 1/2 rpa2t. Us
> In Section 8.5 we calculated the center of mass by considering objects composed of a finite number of point masses or objects that, by symmetry, could be represented by a finite number of point masses. For a solid object whose mass distribution does not
> In a rocket- propulsion problem the mass is variable. Another such problem is a raindrop falling through a cloud of small water droplets. Some of these small droplets adhere to the raindrop, thereby increasing its mass as it falls. The force on the raind
> On a compact disc (CD), music is coded in a pattern of tiny pits arranged in a track that spirals outward toward the rim of the disc. As the disc spins inside a CD player, the track is scanned at a constant linear speed of v = 1.25m/s. Because the radius
> Calculate the moment of inertia of a uniform solid cone about an axis through its center (Fig. P9.90). The cone has mass M and altitude h. The radius of its circular base is R. Fig. P9.90: Figure P9.90 h Axis
> A bicycle wheel has an initial angular velocity of 1.50 rad/s. (a) If its angular acceleration is constant and equal to 0.200 rad/s2, what is its angular velocity at t = 2.50 s? (b) Through what angle has the wheel turned between t = 0 and t = 2.50 s?
> A spring stores potential energy U0 when it is compressed a distance x0 from its uncompressed length. (a) In terms of U0, how much energy does the spring store when it is compressed (i) twice as much and (ii) half as much? (b) In terms of x0, how much mu
> A wheel is rotating about an axis that is in the z-direction. The angular velocity
> The angle u through which a disk drive turns is given by
> At t = 0 the current to a dc electric motor is reversed, resulting in an angular displacement of the motor shaft given by
> A slender rod with length L has a mass per unit length that varies with distance from the left end, where x = 0, according to dm/dx = gx, where g has units of kg/m2. (a) Calculate the total mass of the rod in terms of g and L. (b) Use Eq. (9.20) to calcu
> Use Eq. (9.20) to calculate the moment of inertia of a slender, uniform rod with mass M and length L about an axis at one end, perpendicular to the rod.
> Use Eq. (9.20) to calculate the moment of inertia of a uniform, solid disk with mass M and radius R for an axis perpendicular to the plane of the disk and passing through its center.
> A thin uniform rod of mass M and length L is bent at its center so that the two segments are now perpendicular to each other. Find its moment of inertia about an axis perpendicular to its plane and passing through (a) the point where the two segments mee
> A thin, rectangular sheet of metal has mass M and sides of length a and b. Use the parallel-axis theorem to calculate the moment of inertia of the sheet for an axis that is perpendicular to the plane of the sheet and that passes through one corner of the
> (a) For the thin rectangular plate shown in part (d) of Table 9.2, find the moment of inertia about an axis that lies in the plane of the plate, passes through the center of the plate, and is parallel to the axis shown. (b) Find the moment of inertia of
> A child is pushing a merry-go-round. The angle through which the merry-go-round has turned varies with time according to
> Tendons are strong elastic fibers that attach muscles to bones. To a reasonable approximation, they obey Hooke’s law. In laboratory tests on a particular tendon, it was found that, when a 250-g object was hung from it, the tendon stretched 1.23 cm. (a)
> About what axis will a uniform, balsa-wood sphere have the same moment of inertia as does a thin-walled, hollow, lead sphere of the same mass and radius, with the axis along a diameter?
> Find the moment of inertia of a hoop (a thin-walled, hollow ring) with mass M and radius R about an axis perpendicular to the hoop’s plane at an edge.
> If we multiply all the design dimensions of an object by a scaling factor f, its volume and mass will be multiplied by f3. (a) By what factor will its moment of inertia be multiplied? (b) If a 1/48-scale model has a rotational kinetic energy of 2.5 J, wh
> A uniform 2.00-m ladder of mass 9.00 kg is leaning against a vertical wall while making an angle of 53.0° with the floor. A worker pushes the ladder up against the wall until it is vertical. What is the increase in the gravitational potential energy of t
> A thin, light wire is wrapped around the rim of a wheel (Fig. E9.45). The wheel rotates without friction about a stationary horizontal axis that passes through the center of the wheel. The wheel is a uniform disk with radius R = 0.280 m. An object of mas
> A bucket of mass m is tied to a massless cable that is wrapped around the outer rim of a frictionless uniform pulley of radius R, similar to the system shown in Fig. E9.43. In terms of the stated variables, what must be the moment of inertia of the pulle
> A frictionless pulley has the shape of a uniform solid disk of mass 2.50 kg and radius 20.0 cm. A 1.50-kg stone is attached to a very light wire that is wrapped around the rim of the pulley (Fig. E9.43), and the system is released from rest. (a) How far
> A light, flexible rope is wrapped several times around a hollow cylinder, with a weight of 40.0 N and a radius of 0.25 m, that rotates without friction about a fixed horizontal axis. The cylinder is attached to the axle by spokes of a negligible moment o
> Energy is to be stored in a 70.0-kg flywheel in the shape of a uniform solid disk with radius R = 1.20 m. To prevent structural failure of the flywheel, the maximum allowed radial acceleration of a point on its rim is 3500 m/s2. What is the maximum kinet
> You need to design an industrial turntable that is 60.0 cm in diameter and has a kinetic energy of 0.250 J when turning at 45.0 rpm (rev/min). (a) What must be the moment of inertia of the turntable about the rotation axis? (b) If your workshop makes thi
> A force of 520 N keeps a certain spring stretched a distance of 0.200 m. (a) What is the potential energy of the spring when it is stretched 0.200 m? (b) What is its potential energy when it is compressed 5.00 cm?
> A fan blade rotates with angular velocity given by
> The flywheel of a gasoline engine is required to give up 500 J of kinetic energy while its angular velocity decreases from 650 rev/min to 520 rev/min. What moment of inertia is required?
> A hollow spherical shell has mass 8.20 kg and radius 0.220 m. It is initially at rest and then rotates about a stationary axis that lies along a diameter with a constant acceleration of 0.890 rad/s2. What is the kinetic energy of the shell after it has t
> A uniform sphere with mass 28.0 kg and radius 0.380 m is rotating at constant angular velocity about a stationary axis that lies along a diameter of the sphere. If the kinetic energy of the sphere is 236 J, what is the tangential velocity of a point on t
> A wheel is turning about an axis through its center with constant angular acceleration. Starting from rest, at t = 0, the wheel turns through 8.20 revolutions in 12.0 s. At t = 12.0 s the kinetic energy of the wheel is 36.0 J. For an axis through its cen
> A compound disk of outside diameter 140.0 cm is made up of a uniform solid disk of radius 50.0 cm and area density 3.00 g/cm2 surrounded by a concentric ring of inner radius 50.0 cm, outer radius 70.0 cm, and area density 2.00 g/cm2. Find the moment of i
> An airplane propeller is 2.08 m in length (from tip to tip) with mass 117 kg and is rotating at 2400 rpm (rev/min) about an axis through its center. You can model the propeller as a slender rod. (a) What is its rotational kinetic energy? (b) Suppose that
> A wagon wheel is constructed as shown in Fig. E9.33. The radius of the wheel is 0.300 m, and the rim has mass 1.40 kg. Each of the eight spokes that lie along a diameter and are 0.300 m long has mass 0.280 kg. What is the moment of inertia of the wheel a
> You are a project manager for a manufacturing company. One of the machine parts on the assembly line is a thin, uniform rod that is 60.0 cm long and has mass 0.400 kg. (a) What is the moment of inertia of this rod for an axis at its center, perpendicular
> A uniform bar has two small balls glued to its ends. The bar is 2.00 m long and has mass 4.00 kg, while the balls each have mass 0.300 kg and can be treated as point masses. Find the moment of inertia of this combination about an axis (a) perpendicular t
> An ideal spring of negligible mass is 12.00 cm long when nothing is attached to it. When you hang a 3.15-kg weight from it, you measure its length to be 13.40 cm. If you wanted to store 10.0 J of potential energy in this spring, what would be its total l
> Small blocks, each with mass m, are clamped at the ends and at the center of a rod of length L and negligible mass. Compute the moment of inertia of the system about an axis perpendicular to the rod and passing through (a) the center of the rod and (b) a
> The angular velocity of a flywheel obeys the equation
> Calculate the moment of inertia of each of the following uniform objects about the axes indicated. Consult Table 9.2 as needed. (a) A thin 2.50-kg rod of length 75.0 cm, about an axis perpendicular to it and passing through (i) one end and (ii) its cente
> Four small spheres, each of which you can regard as a point of mass 0.200 kg, are arranged in a square 0.400 m on a side and connected by extremely light rods (Fig. E9.28). Find the moment of inertia of the system about an axis (a) through the center of
> According to the shop manual, when drilling a 12.7-mm-diameter hole in wood, plastic, or aluminum, a drill should have a speed of 1250 rev/min. For a 12.7-mm- diameter drill bit turning at a constant 1250 rev/min, find (a) the maximum linear speed of any
> At t = 3.00 s a point on the rim of a 0.200-m-radius wheel has a tangential speed of 50.0 m/s as the wheel slows down with a tangential acceleration of constant magnitude 10.0 m/s2. (a) Calculate the wheel’s constant angular acceleration. (b) Calculate t
> An advertisement claims that a centrifuge takes up only 0.127 m of bench space but can produce a radial acceleration of 3000g at 5000 rev/min. Calculate the required radius of the centrifuge. Is the claim realistic?
> An electric turntable 0.750 m in diameter is rotating about a fixed axis with an initial angular velocity of 0.250 rev>s and a constant angular acceleration of 0.900 rev/s2. (a) Compute the angular velocity of the turntable after 0.200 s. (b) Through how
> A flywheel with a radius of 0.300 m starts from rest and accelerates with a constant angular acceleration of 0.600 rad/s2. Compute the magnitude of the tangential acceleration, the radial acceleration, and the resultant acceleration of a point on its rim
> You are to design a rotating cylindrical axle to lift 800-N buckets of cement from the ground to a rooftop 78.0 m above the ground. The buckets will be attached to a hook on the free end of a cable that wraps around the rim of the axle; as the axle turns
> A 10.0-kg microwave oven is pushed 6.00 m up the sloping surface of a loading ramp inclined at an angle of 36.9° above the horizontal, by a constant force

