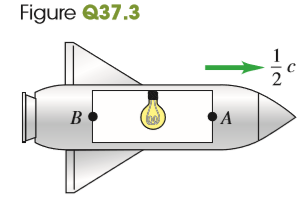
Question: A rocket is moving to the right
A rocket is moving to the right at 1/2 the speed of light relative to the earth. A light bulb in the center of a room inside the rocket suddenly turns on. Call the light hitting the front end of the room event A and the light hitting the back of the room event B (Fig. Q37.3). Which event occurs first, A or B, or are they simultaneous, as viewed by
a. an astronaut riding in the rocket and
b. a person at rest on the earth?
Transcribed Image Text:
Figure Q37.3 В A -IN
> A photon of frequency f undergoes Compton scattering from an electron at rest and scatters through an angle ɸ. The frequency of the scattered photon is f ′. How is f ′ related to f? Does your answer depend on ɸ? Explain.
> The materials called phosphors that coat the inside of a fluorescent lamp convert ultraviolet radiation (from the mercury vapor discharge inside the tube) into visible light. Could one also make a phosphor that converts visible light to ultraviolet? Expl
> In an experiment involving the photoelectric effect, if the intensity of the incident light (having frequency higher than the threshold frequency) is reduced by a factor of 10 without changing anything else, which (if any) of the following statements abo
> Explain why Fig. 38.4 shows that most photoelectrons have kinetic energies less than hf - ɸ, and also explain how these smaller kinetic energies occur.
> Consider Compton scattering of a photon by a moving electron. Before the collision the photon has wavelength λ and is moving in the +x-direction, and the electron is moving in the –x-direction with total energy E (including
> A spherical, concave shaving mirror has a radius of curvature of 32.0 cm. a. What is the magnification of a person’s face when it is 12.0 cm to the left of the vertex of the mirror? b. Where is the image? Is the image real or virtual? c. Draw a princip
> The starships of the Solar Federation are marked with the symbol of the federation, a circle, while starships of the Denebian Empire are marked with the empire’s symbol, an ellipse whose major axis is 1.40 times longer than its minor ax
> After being produced in a collision between elementary particles, a positive pion (π+) must travel down a 1.90-km-long tube to reach an experimental area. A π+ particle has an average lifetime (measured in its rest frame) of 2.60 * 10-8 s; the π+ we are
> You are a scientist studying small aerosol particles that are contained in a vacuum chamber. The particles carry a net charge, and you use a uniform electric field to exert a constant force of 8.00 * 10-14 N on one of them. That particle moves in the dir
> You are an astronomer investigating four astronomical sources of infrared radiation. You have identified the nature of each source, so you know the frequency f0 of each when it is at rest relative to you. Your detector, which is at rest relative to the e
> As a research scientist at a linear accelerator, you are studying an unstable particle. You measure its mean lifetime ∆t as a function of the particle’s speed relative to your laboratory equipment. You record the speed
> The French physicist Armand Fizeau was the first to measure the speed of light accurately. He also found experimentally that the speed, relative to the lab frame, of light traveling in a tank of water that is itself moving at a speed V relative to the la
> A spaceship moving at constant speed u relative to us broadcasts a radio signal at constant frequency f0. As the spaceship approaches us, we receive a higher frequency f; after it has passed, we receive a lower frequency. a. As the spaceship passes by,
> A baseball coach uses a radar device to measure the speed of an approaching pitched baseball. This device sends out electromagnetic waves with frequency f0 and then measures the shift in frequency ∆f of the waves reflected from the moving baseball. If th
> Einstein and Lorentz, being avid tennis players, play a fast-paced game on a court where they stand 20.0 m from each other. Being very skilled players, they play without a net. The tennis ball has mass 0.0580 kg. You can ignore gravity and assume that th
> Two events are observed in a frame of reference S to occur at the same space point, the second occurring 1.80 s after the first. In a frame S′ moving relative to S, the second event is observed to occur 2.15 s after the first. What is the difference betw
> Suppose that in the situation of Example 34.7 of Section 34.3 (see Fig. 34.26) a vertical arrow 2.00 m tall is painted on the side of the pool beneath the water line. According to the calculations in the example, this arrow would appear to the person sho
> In the earth’s rest frame, two protons are moving away from each other at equal speed. In the frame of each proton, the other proton has a speed of 0.700c. What does an observer in the rest frame of the earth measure for the speed of each proton?
> The distance to a particular star, as measured in the earth’s frame of reference, is 7.11 light-years (1 light-year is the distance that light travels in 1 y). A spaceship leaves the earth and takes 3.35 y to arrive at the star, as measured by passengers
> Two atomic clocks are carefully synchronized. One remains in New York, and the other is loaded on an airliner that travels at an average speed of 250 m/s and then returns to New York. When the plane returns, the elapsed time on the clock that stayed behi
> The net force F on a particle of mass m is directed at 30.0° counterclockwise from the +x-axis. At one instant of time, the particle is traveling in the +x-direction with a speed (measured relative to the earth) of 0.700c. At this instant, what is the di
> A muon is created 55.0 km above the surface of the earth (as measured in the earth’s frame). The average lifetime of a muon, measured in its own rest frame, is 2.20 µs, and the muon we are considering has this lifetime. In the frame of the muon, the eart
> A space probe is sent to the vicinity of the star Capella, which is 42.2 light-years from the earth. (A light-year is the distance light travels in a year.) The probe travels with a speed of 0.9930c. An astronaut recruit on board is 19 years old when the
> A cube of metal with sides of length a sits at rest in a frame S with one edge parallel to the x-axis. Therefore, in S the cube has volume a3. Frame S′ moves along the x-axis with a speed u. As measured by an observer in frame S′, what is the volume of t
> In the alternate universe, how fast must an object be moving for it to have a kinetic energy equal to its rest mass? a. 225 m/s; b. 260 m/s; c. 300 m/s; d. The kinetic energy could not be equal to the rest mass.
> If the airplane of Passage Problem 37.71 has a rest mass of 20,000 kg, what is its relativistic mass when the plane is moving at 180 m/s ? a. 8000 kg; b. 12,000 kg; c. 16,000 kg; d. 25,000 kg; e. 33,300 kg. From Passage Problem 37.71 An airplane h
> An airplane has a length of 60 m when measured at rest. When the airplane is moving at 180 m/s (400 mph) in the alternate universe, how long would the plane appear to be to a stationary observer? a. 24 m; b. 36 m; c. 48 m; d. 60 m; e. 75 m.
> In Example 34.4 (Section 34.2), there appears to be an ambiguity for the case s = 10 cm as to whether s ′ is +∞ or -∞ and whether the image is erect or inverted. How is this resolved? Or is it? From
> A spaceship flies past Mars with a speed of 0.985c relative to the surface of the planet. When the spaceship is directly overhead, a signal light on the Martian surface blinks on and then off. An observer on Mars measures that the signal light was on for
> The positive muon (µ+), an unstable particle, lives on average 2.20 * 10-6 s (measured in its own frame of reference) before decaying. a. If such a particle is moving, with respect to the laboratory, with a speed of 0.900c, what average lifetime is meas
> Suppose the two lightning bolts shown in Fig. 37.5a are simultaneous to an observer on the train. Show that they are not simultaneous to an observer on the ground. Which lightning strike does the ground observer measure to come first? Lightning hits
> The sun produces energy by nuclear fusion reactions, in which matter is converted into energy. By measuring the amount of energy we receive from the sun, we know that it is producing energy at a rate of 3.8 * 1026 W. a. How many kilograms of matter does
> What is the kinetic energy of a proton moving at a. 0.100c; b. 0.500c; c. 0.900c? How much work must be done to d. increase the proton’s speed from 0.100c to 0.500c and e. increase the proton’s speed from 0.500c to 0.900c? f. How do the last two re
> Two protons (each with rest mass M = 1.67 * 10-27 kg) are initially moving with equal speeds in opposite directions. The protons continue to exist after a collision that also produces an h0 particle (see Chapter 44). The rest mass of the h0 is m = 9.75 *
> A particle has rest mass 6.64 * 10-27 kg and momentum 2.10 * 10-18 kg.m/s. a. What is the total energy (kinetic plus rest energy) of the particle? b. What is the kinetic energy of the particle? c. What is the ratio of the kinetic energy to the rest en
> Electrons are accelerated through a potential difference of 750 kV, so that their kinetic energy is 7.50 * 105 eV. a. What is the ratio of the speed v of an electron having this energy to the speed of light, c? b. What would the speed be if it were com
> To determine whether a frog can judge distance by means of the amount its lens must move to focus on an object, researchers covered one eye with an opaque material. An insect was placed in front of the frog, and the distance that the frog snapped its ton
> Given that frogs are nearsighted in air, which statement is most likely to be true about their vision in water? a. They are even more nearsighted; because water has a higher index of refraction than air, a frog’s ability to focus light increases in wate
> A person looks at his reflection in the concave side of a shiny spoon. Is it right side up or inverted? Does it matter how far his face is from the spoon? What if he looks in the convex side? (Try this yourself!)
> What is the farthest distance at which a typical “nearsighted” frog can see clearly in air? a. 12 m; b. 6.0 m; c. 80 cm; d. 17 cm.
> A frog can see an insect clearly at a distance of 10 cm. At that point the effective distance from the lens to the retina is 8 mm. If the insect moves 5 cm farther from the frog, by how much and in which direction does the lens of the frog’s eye have to
> People with normal vision cannot focus their eyes underwater if they aren’t wearing a face mask or goggles and there is water in contact with their eyes (see Discussion Question Q34.23). a. Why not? b. With the simplified model of the eye described in
> a. How much work must be done on a particle with mass m to accelerate it (a) from rest to a speed of 0.090c and b. from a speed of 0.900c to a speed of 0.990c ? (Express the answers in terms of mc2.) c. How do your answers in parts (a) and (b) compare?
> a. For a lens with focal length f, find the smallest distance possible between the object and its real image. b. Graph the distance between the object and the real image as a function of the distance of the object from the lens. Does your graph agree wit
> The science museum where you work is constructing a new display. You are given a glass rod that is surrounded by air and was ground on its left-hand end to form a hemispherical surface there. You must determine the radius of curvature of that surface and
> It is your first day at work as a summer intern at an optics company. Your supervisor hands you a diverging lens and asks you to measure its focal length. You know that with a converging lens, you can measure the focal length by placing an object a dista
> In setting up an experiment for a high school biology lab, you use a concave spherical mirror to produce real images of a 4.00-mm-tall firefly. The firefly is to the right of the mirror, on the mirror’s optic axis, and serves as a real
> Figure P34.101 shows a simple version of a zoom lens. The converging lens has focal length f1 and the diverging lens has focal length f2 = - f2 . The two lenses are separated by a variable distance d that is always less than f1 Also, the magnitude of the
> Figure P34.100 is a diagram of a Galilean telescope, or opera glass, with both the object and its final image at infinity. The image I serves as a virtual object for the eyepiece. The final image is virtual and erect. a. Prove that the angular magnifica
> A spherical mirror is cut in half horizontally. Will an image be formed by the bottom half of the mirror? If so, where will the image be formed?
> A shaft is drilled from the surface to the center of the earth. As in Example 13.10 (Section 13.6), make the unrealistic assumption that the density of the earth is uniform. With this approximation, the gravitational force on an object with mass m, that
> A uniform wire with mass M and length L is bent into a semicircle. Find the magnitude and direction of the gravitational force this wire exerts on a point with mass m placed at the center of curvature of the semicircle.
> An object in the shape of a thin ring has radius a and mass M. A uniform sphere with mass m and radius R is placed with its center at a distance x to the right of the center of the ring, along a line through the center of the ring, and perpendicular to i
> One of the brightest comets of the 20th century was Comet Hyakutake, which passed close to the sun in early 1996. The orbital period of this comet is estimated to be about 30,000 years. Find the semi-major axis of this comet’s orbit. Compare it to the av
> Planets are not uniform inside. Normally, they are densest at the center and have decreasing density outward toward the surface. Model a spherically symmetric planet, with the same radius as the earth, as having a density that decreases linearly with dis
> A satellite with mass 848 kg is in a circular orbit with an orbital speed of 9640 m/s around the earth. What is the new orbital speed after friction from the earth’s upper atmosphere has done -7.50 × 109 J of work on the satellite? Does the speed increas
> A 5000-kg spacecraft is in a circular orbit 2000 km above the surface of Mars. How much work must the spacecraft engines perform to move the spacecraft to a circular orbit that is 4000 km above the surface?
> A rocket with mass 5.00 × 103 kg is in a circular orbit of radius 7.20 × 106 m around the earth. The rocket’s engines fire for a period of time to increase that radius to 8.80 * 106 m, with the orbit again circular. (a) What is the change in the rocket’s
> Consider a spacecraft in an elliptical orbit around the earth. At the low point, or perigee, of its orbit, it is 400 km above the earth’s surface; at the high point, or apogee, it is 4000 km above the earth’s surface. (a) What is the period of the spacec
> The planet Uranus has a radius of 25,360 km and a surface acceleration due to gravity of 9.0 m>s2 at its poles. Its moon Miranda (discovered by Kuiper in 1948) is in a circular orbit about Uranus at an altitude of 104,000 km above the planet’s surface. M
> At what point in the motion of a simple pendulum is the string tension greatest? Least? In each case give the reasoning behind your answer.
> Comets travel around the sun in elliptical orbits with large eccentricities. If a comet has speed 2.0 × 104 m/s when at a distance of 2.5 × 1011 m from the center of the sun, what is its speed when at a distance of 5.0 × 1010 m?
> Two stars, with masses M1 and M2, are in circular orbits around their center of mass. The star with mass M1 has an orbit of radius R1; the star with mass M2 has an orbit of radius R2. (a) Show that the ratio of the orbital radii of the two stars equals t
> Two identical stars with mass M orbit around their center of mass. Each orbit is circular and has radius R, so that the two stars are always on opposite sides of the circle. (a) Find the gravitational force of one star on the other. (b) Find the orbital
> The preceding problems in this chapter have assumed that the springs had negligible mass. But of course no spring is completely massless. To find the effect of the spring’s mass, consider a spring with mass M, equilibrium length L0, and spring constant k
> Two springs with the same unstretched length but different force constants k1 and k2 are attached to a block with mass m on a level, frictionless surface. Calculate the effective force constant keff in each of the three cases (a), (b), and (c) depicted i
> On July 4, 2005, the NASA spacecraft Deep Impact fired a projectile onto the surface of Comet Tempel 1. This comet is about 9.0 km across. Observations of surface debris released by the impact showed that dust with a speed as low as 1.0 m/s was able to e
> An unmanned spacecraft is in a circular orbit around the moon, observing the lunar surface from an altitude of 50.0 km (see Appendix F). To the dismay of scientists on earth, an electrical fault causes an on-board thruster to fire, decreasing the speed o
> The 0.100-kg sphere in Fig. P13.58 is released from rest at the position shown in the sketch, with its center 0.400 m from the center of the 5.00-kg mass. Assume that the only forces on the 0.100-kg sphere are the gravitational forces exerted by the othe
> You are exploring a distant planet. When your spaceship is in a circular orbit at a distance of 630 km above the planet’s surface, the ship’s orbital speed is 4900 m/s. By observing the planet, you determine its radius to be 4.48 × 106 m. You then land o
> Your starship, the Aimless Wanderer, lands on the mysterious planet Mongo. As chief scientist-engineer, you make the following measurements: A 2.50-kg stone thrown upward from the ground at 12.0 m/s returns to the ground in 4.80 s; the circumference of M
> Can a standing wave be produced on a string by superposing two waves traveling in opposite directions with the same frequency but different amplitudes? Why or why not? Can a standing wave be produced by superposing two waves traveling in opposite directi
> An astronaut, whose mission is to go where no one has gone before, lands on a spherical planet in a distant galaxy. As she stands on the surface of the planet, she releases a small rock from rest and finds that it takes the rock 0.480 s to fall 1.90 m. I
> (a) Suppose you are at the earth’s equator and observe a satellite passing directly overhead and moving from west to east in the sky. Exactly 12.0 hours later, you again observe this satellite to be directly overhead. How far above the earth’s surface is
> Planet X rotates in the same manner as the earth, around an axis through its north and south poles, and is perfectly spherical. An astronaut who weighs 943.0 N on the earth weighs 915.0 N at the north pole of Planet X and only 850.0 N at its equator. The
> A landing craft with mass 12,500 kg is in a circular orbit 5.75 × 105 m above the surface of a planet. The period of the orbit is 5800 s. The astronauts in the lander measure the diameter of the planet to be 9.60 × 106 m. The lander sets down at the nort
> What is the escape speed from a 300-km-diameter asteroid with a density of 2500 kg/m3?
> Mass M is distributed uniformly over a disk of radius a. Find the gravitational force (magnitude and direction) between this disk-shaped mass and a particle with mass m located a distance x above the center of the disk (Fig. P13.81). Does your result red
> An astronaut inside a spacecraft, which protects her from harmful radiation, is orbiting a black hole at a distance of 120 km from its center. The black hole is 5.00 times the mass of the sun and has a Schwarzschild radius of 15.0 km. The astronaut is po
> The most efficient way to send a spacecraft from the earth to another planet is to use a Hohmann transfer orbit (Fig. P13.79). If the orbits of the departure and destination planets are circular, the Hohmann transfer orbit is an elliptical orbit whose pe
> For a planet in our solar system, assume that the axis of orbit is at the sun and is circular. Then the angular momentum about that axis due to the planet’s orbital motion is L = MvR. (a) Derive an expression for L in terms of the planet’s mass M, orbita
> A deep-sea diver is suspended beneath the surface of Loch Ness by a 100-m-long cable that is attached to a boat on the surface (Fig. P15.77). The diver and his suit have a total mass of 120 kg and a volume of 0.0800 m3. The cable has a diameter of 2.00 c
> A planet makes a circular orbit with period T around a star. If the planet were to orbit at the same distance around this star, but the planet had three times as much mass, what would the new period (in terms of T) be: (a) 3T, (b) T√3, (c) T, (d) T/√3,
> You are measuring the frequency dependence of the average power Pav transmitted by traveling waves on a wire. In your experiment you use a wire with linear mass density 3.5 g/m. For a transverse wave on the wire with amplitude 4.0 mm, you measure Pav (in
> In your physics lab, an oscillator is attached to one end of a horizontal string. The other end of the string passes over a frictionless pulley. You suspend a mass M from the free end of the string, producing tension Mg in the string. The oscillator prod
> Scale length is the length of the part of a guitar string that is free to vibrate. A standard value of scale length for an acoustic guitar is 25.5 in. The frequency of the fundamental standing wave on a string is determined by the stringâ€
> A musician tunes the C-string of her instrument to a fundamental frequency of 65.4 Hz. The vibrating portion of the string is 0.600 m long and has a mass of 14.4 g. (a) With what tension must the musician stretch it? (b) What percent increase in tension
> A string or rope will break apart if it is placed under too much tensile stress [see Eq. (11.8)]. Thicker ropes can withstand more tension without breaking because the thicker the rope, the greater the cross-sectional area and the smaller the stress. One
> A large rock that weighs 164.0 N is suspended from the lower end of a thin wire that is 3.00 m long. The density of the rock is 3200 kg/m3. The mass of the wire is small enough that its effect on the tension in the wire can be ignored. The upper end of t
> A string with both ends held fixed is vibrating in its third harmonic. The waves have a speed of 192 m/s and a frequency of 240 Hz. The amplitude of the standing wave at an antinode is 0.400 cm. (a) Calculate the amplitude at points on the string a dista
> A uniform cylindrical steel wire, 55.0 cm long and 1.14 mm in diameter, is fixed at both ends. To what tension must it be adjusted so that, when vibrating in its first overtone, it produces the note D-sharp of frequency 311 Hz? Assume that it stretches a
> A guitar string is vibrating in its fundamental mode, with nodes at each end. The length of the segment of the string that is free to vibrate is 0.386 m. The maximum transverse acceleration of a point at the middle of the segment is 8.40 × 103 m/s2 and t
> A thin string 2.50 m in length is stretched with a tension of 90.0 N between two supports. When the string vibrates in its first overtone, a point at an antinode of the standing wave on the string has an amplitude of 3.50 cm and a maximum transverse spee
> If a projectile is fired straight up from the earth’s surface, what would happen if the total mechanical energy (kinetic plus potential) is (a) less than zero, and (b) greater than zero? In each case, ignore air resistance and the gravitational effects o
> A strong string of mass 3.00 g and length 2.20 m is tied to supports at each end and is vibrating in its fundamental mode. The maximum transverse speed of a point at the middle of the string is 9.00 m/s. The tension in the string is 330 N. (a) What is th
> Clothesline Nodes. Cousin Throckmorton is once again playing with the clothesline in Example 15.2 (Section 15.3). One end of the clothesline is attached to a vertical post. Throcky holds the other end loosely in his hand, so the speed of waves on the cl
> A vibrating string 50.0 cm long is under a tension of 1.00 N. The results from five successive stroboscopic pictures are shown in Fig. P15.64. The strobe rate is set at 5000 flashes per minute, and observations reveal that the maximum displacement occurr
> A sinusoidal transverse wave travels on a string. The string has length 8.00 m and mass 6.00 g. The wave speed is 30.0 m>s, and the wavelength is 0.200 m. (a) If the wave is to have an average power of 50.0 W, what must be the amplitude of the wave? (b)
> A vertical, 1.20-m length of 18-gauge (diameter of 1.024 mm) copper wire has a 100.0-N ball hanging from it. (a) What is the wavelength of the third harmonic for this wire? (b) A 500.0-N ball now replaces the original ball. What is the change in the wave
> A horizontal wire is tied to supports at each end and vibrates in its second-overtone standing wave. The tension in the wire is 5.00 N, and the node-to-node distance in the standing wave is 6.28 cm. (a) What is the length of the wire? (b) A point at an a

