Question: A spirogram is a device that records
A spirogram is a device that records on a graph the volume of air in a person’s lungs as a function of time. If a person undergoes spontaneous hyperventilation, the spirogram trace will closely approximate a sine curve. A typical trace is given by
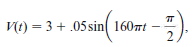
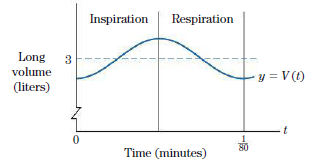
where t is measured in minutes and V(t) is the lung volume in liters. (See Fig. 1.) Exercise refers to this function.
Figure 1:
The minute volume is defined as the total amount of air inspired (breathed in) during 1 minute. According to a standard text on respiratory physiology, when a person undergoes spontaneous hyperventilation, the peak inspiratory flow equals p times the minute volume, and the mean inspiratory flow equals twice the minute volume. Verify these assertions using the data from Exercise 57.
Exercise 57:
(a) Find a formula for the rate of flow of air into the lungs at time t.
(b) Find the maximum rate of flow of air during inspiration (breathing in). This quantity is called the peak inspiratory flow.
(c) Inspiration occurs during the time from t = 0 to t = 1/160. Find the average rate of flow of air during inspiration. This quantity is called the mean inspiratory flow.
Transcribed Image Text:
V(t) = 3+.05 sin 160mt 05 sin(16 -7). 2 Long volume (liters) 3 0 Inspiration Respiration Time (minutes) - 80 y = V(t) t
> Find all points (x, y) where f (x, y) has a possible relative maximum or minimum. f (x, y) = x2 - 5xy + 6y2 + 3x - 2y + 4
> Find ∂f/∂x and ∂f/∂y for each of the following functions. f (x, y) = ex/(1 + ey)
> Find ∂f/∂x and ∂f/∂y for each of the following functions. f (x, y) = (2x - y + 5)2
> Find ∂f/∂x and ∂f/∂y for each of the following functions. f (x, y) = 1/(x + y)
> Find ∂f/∂x and ∂f/∂y for each of the following functions. f (x, y) = x/y + y/x
> Find ∂f/∂x and ∂f/∂y for each of the following functions. f (x, y) = x exy
> Let f (x, y) = xy. Show that f (2, 3 + k) - f (2, 3) = 2k.
> Find ∂f/∂x and ∂f/∂y for each of the following functions. f (x, y) = 2x2ey
> Find ∂f/∂x and ∂f/∂y for each of the following functions. f (x, y) = x2 - y2
> Find ∂f/∂x and ∂f/∂y for each of the following functions. f (x, y) = 5xy
> The productivity of a country is given by f (x, y) = 300x2/3y1/3, where x and y are the amount of labor and capital. (a) Compute the marginal productivities of labor and capital when x = 125 and y = 64. (b) Use part (a) to determine the approximate effec
> A farmer can produce f (x, y) = 200 √(6x2 + y2) units of produce by utilizing x units of labor and y units of capital. (The capital is used to rent or purchase land, materials, and equipment.) (a) Calculate the marginal productivities of labor and capita
> Let f (x, y) = xey + x4y + y3. Find ∂2f/∂x2, ∂2f/∂y2, ∂2f/∂x∂y, and ∂2f/∂y∂x.
> Let f (x, y) = x3y + 2xy2. Find ∂2f/∂x2, ∂2f/∂y2, ∂2f/∂x∂y, and ∂2f/∂y∂x.
> Let f (x, y) = x/(y – 6). Compute ∂f/∂y (2, 1) and interpret your result.
> Let f (x, y) = xy2 + 5. Evaluate ∂f/∂y at (x, y) = (2, -1) and interpret your result.
> Let f (x, y) = (x + y2)3. Evaluate ∂f/∂x and ∂f/∂y at (x, y) = (1, 2).
> Let f (x, y) = xy. Show that f (2 + h, 3) - f (2, 3) = 3h.
> Let f (x, y) = x2 + 2xy + y2 + 3x + 5y. Find ∂f/∂x (2, -3) and ∂f/∂x (2, -3).
> Let f (x, y, z) = xy/z. Find ∂f/∂x, ∂f/∂y, and ∂f/∂z.
> Construct angles with the following radian measure. -π
> Determine the radian measure of the angle shown.
> Determine the radian measure of the angle shown.
> Determine the radian measure of the angle shown.
> Evaluate the given integral. ∫0 π/4 (2 + 2 tan2 x) dx
> Let f (x, y, z) = xz eyz. Find ∂f/∂x, ∂f/∂y, and ∂f/∂z.
> Evaluate the given integral. ∫0 π/4 tan2 x dx
> Evaluate the given integral. ∫ (2 + tan2 x) dx
> Evaluate the given integral. ∫ (1 + tan2 x) dx
> Evaluate the given integral. ∫ tan2 3x dx
> Evaluate the given integral. ∫ tan2 x dx
> Find the average of the function f (t) over the given interval. f (t) = cos t + sin t, - π ≤ t ≤ 0
> Find the average of the function f (t) over the given interval. f (t) = 1000 + 200 sin 2 (t - π /4), 0 ≤ t ≤ 3 π /4
> Find the average of the function f (t) over the given interval. f (t) = t - cos 2t, 0 ≤ t ≤ π
> Find the average of the function f (t) over the given interval. f (t) = 1 + sin 2t – 1/3 cos 2t, 0 ≤ t ≤ 2π
> In Fig. 2: Find the shaded area A4. Figure 2: 1 Y 0 A₁ cosx TU2 A3 sin x X
> Let f (x, y, z) = zex/y. Find ∂f/∂x, ∂f/∂y, and ∂f/∂z.
> In Fig. 2: Find the shaded area A3. Figure 2: 1 Y 0 A₁ cosx TU2 A3 sin x X
> In Fig. 2: Find the shaded area A2. Figure 2: 1 Y 0 A₁ cosx TU2 A3 sin x X
> In Fig. 2: Find the shaded area A1. Figure 2: 1 Y 0 A₁ cosx TU2 A3 sin x X
> Evaluate the following integrals. ∫ 2 sec2 2x dx
> Evaluate the following integrals. ∫ sec2 x/2 dx
> Evaluate the following integrals. ∫-π π (cos 3x + 2 sin 7x) dx
> Evaluate the following integrals. ∫0 π (x - 2 cos (π - 2x))
> Evaluate the following integrals. ∫ cos (6 - 2x) dx
> Evaluate the following integrals. ∫0 π /2 cos 6x dx
> Evaluate the following integrals. ∫ (3 cos 3x - 2 sin 2x) dx
> Let f (x, y, z) = (1 + x2y)/z. Find ∂f/∂x, ∂f/∂y, and ∂f/∂z.
> Evaluate the following integrals. ∫ sin (π - x) dx
> A spirogram is a device that records on a graph the volume of air in a person’s lungs as a function of time. If a person undergoes spontaneous hyperventilation, the spirogram trace will closely approximate a sine curve. A typical trace
> A spirogram is a device that records on a graph the volume of air in a person’s lungs as a function of time. If a person undergoes spontaneous hyperventilation, the spirogram trace will closely approximate a sine curve. A typical trace
> Find the area of the region bounded by the curves y = x and y = sin x from x = 0 to x = π.
> Find the area of the region between the curve y = cos t and the t-axis from t = 0 to t = 3π/2.
> Find the area of the region between the curve y = sin t and the t-axis from t = 0 to t = 2π.
> Find the area under the curve y = 2 + sin 3t from t = 0 to t = π/2.
> Sketch the graph of y = t + sin t for 0 ≤ t ≤ 2π.
> Find the equation of the line tangent to the graph of y = tan t at t = π/4.
> Let f (p, q) = 1 - p(1 + q). Find ∂f/∂q and ∂f/∂p.
> The identity sin (s + t) = sin s cos t + cos s sin t was given in Section 8.2. Compute the partial derivative of each side with respect to t, and obtain an identity involving cos (s + t).
> If f (s, t) = t sin st, find ∂f/∂s and ∂f/∂t.
> If z = sin wt, find ∂z/∂w and ∂z/∂t.
> If f (s, t) = sin s cos 2t, find ∂f/∂s and ∂f/∂t.
> Show that y = 3 sin 2t + cos 2t satisfies the differential equation y’’ = -4y.
> If f (t) = sin2 t, find f ‘(t).
> f (t) = et tan t
> f (t) = etan t
> Differentiate (with respect to t or x): f (t) = tan 2t / cos t
> Differentiate (with respect to t or x): f (t) = sin t / tan 3t
> Let f (L, K) = 3√(LK). Find ∂f/∂L.
> Differentiate (with respect to t or x): y = sin4 e3x
> Differentiate (with respect to t or x): y = e3x sin4 x
> Differentiate (with respect to t or x): y = ln (cos x)
> Differentiate (with respect to t or x): y = ln (sin x)
> Differentiate (with respect to t or x): y = ln x cos x
> Differentiate (with respect to t or x): y = sin x tan x
> Differentiate (with respect to t or x): y = tan (sin x)
> Differentiate (with respect to t or x): y = sin (tan x)
> Differentiate (with respect to t or x): y = tan e-2x
> Differentiate (with respect to t or x): y = tan (x4 + x2)
> Find ∂f/∂x and ∂f/∂y for each of the following functions. f (x, y) = √(x2 + y2)
> Differentiate (with respect to t or x): f (x) = tan3 2x
> Differentiate (with respect to t or x): f (x) = cos3 4x
> Differentiate (with respect to t or x): f (x) = (cos x – 1) / x3
> Differentiate (with respect to t or x): f (x) = cos 2x / sin 3x
> Differentiate (with respect to t or x): g(x) = sin(-2x) cos 5x
> Differentiate (with respect to t or x): g(x) = x3 sin x
> Differentiate (with respect to t or x): f (t) = cos t3
> Differentiate (with respect to t or x): f (t) = sin√t
> Differentiate (with respect to t or x): f (t) = sin 3t
> Differentiate (with respect to t or x): f (t) = 3 sin t
> Find ∂f/∂x and ∂f/∂y for each of the following functions. f (x, y) = (x – y)/(x + y)
> Determining the height of a Tree A tree casts a 60-foot shadow when the angle of elevation of the sun (measured from the horizontal) is 53˚ . How tall is the tree?
> Geometry of a roof A gabled roof is to be built on a house that is 30 feet wide so that the roof rises at a pitch of 23˚ . Determine the length of the rafters needed to support the roof.
> When π /2 < t < π, is sin t positive or negative?
> When – π/2 < t < 0, is tan t positive or negative?
> Find the four values of t between -2π and 2π at which sin t = -cos t.
> Find the four values of t between -2π and 2π at which sin t = cos t.
> If cos t = - 2/3, what are the possible values for sin t?
> If sin t = 1/5, what are the possible values for cos t?
> The point with the given coordinates determines an angle of t radians, where 0 ≤ t ≤ 2π. Find sin t, cos t, and tan t. (3, -4)

