Question: A study of traffic delays in 68
A study of traffic delays in 68 U.S. cities found the following relationship between Total Delay (in total hours lost) and Mean Highway Speed:
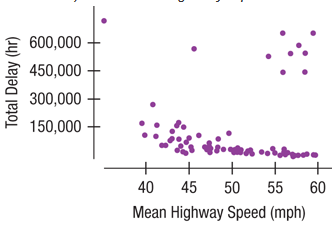
Is it appropriate to summarize the strength of association with a correlation? Explain.
> The scatterplot shows the gross domestic product (GDP) of the United States in trillions of 2009 dollars plotted against years since 1950 A linear model fit to the relationship looks like this: Dependent variable is: GDP($T) R-squared = 96.9% s = 0.8137
> In Exercise 58 we looked at United Nations data about a country GDP and the average number of people per room (Crowdedness) in housing there. For a re-expression, a student tried the reciprocal 10000|sol|GDP, representing the number of people per $10,000
> Let try the re-expressed variable Fuel Consumption (gal/100 mi) to examine the fuel efficiency of the 11 cars in Exercise 57. Here are the revised regression analysis and residuals plot: Dependent variable is: Fuel Consumption R-squared = 89.2% 1. Explai
> In a Chance magazine article (Summer 2005), Danielle Vasilescu and Howard Wainer used data from the United Nations Center for Human Settlements to investigate aspects of living conditions for several countries. Among the variables they looked at were the
> Hurricane Katrina hurricane force winds extended 120 miles from its center. Katrina was a big storm, and that affects how we think about the prediction errors. Suppose we add 120 miles to each error to get an idea of how far from the predicted track we m
> Now consider the variables igÆ’ and weight in the data set Igf13. 1. Fit a regression model. If the data violate any assumptions, find a suitable re-expression of igÆ’. 2. Add sex to the model in part a as a predictor. Interpret the coefficient of sex. 3
> As the example in the chapter indicates, one of the important factors determining a car Fuel Efficiency is its Weight. Let examine this relationship again, for 11 cars. 1. Describe the association between these variables shown in the scatterplot at the t
> In Chapter 4, we examined Consider the wind speeds in the Hopkins Forest over the course of a year. Here the scatterplot we saw then: (Data in Hopkins Forest) 1. Describe the pattern you see here. 2. Should we try re-expressing either variable to make th
> In Exercise 29, we considered whether a linear model would be appropriate to describe the trend in the number of passengers departing from the Oakland (CA) airport each month since the start of 1997. If we fit a regression model, we obtain this residual
> Look once more at the data from Tour de France 2016. In Exercise 52, we looked at the whole history of the race, but now let consider just the modern era from 1967 on. 1. Make a scatterplot and find the regression of Avg Speed by Year only for years from
> The Consumer Price Index (CPI) tracks the prices of consumer goods in the United States, as shown in the following table. The CPI is reported monthly, but we can look at selected values. The table shows the January CPI at five-year intervals. It indicate
> We met the Tour de France dataset in Chapter 1 (in Just Checking). Look at the Tour de France dataset. One hundred years ago, the fastest rider finished the course at an average speed of about 25.3 kph (around 15.8 mph). By the 21st century, winning ride
> The World Bank reports many demographic statistics about countries of the world. The data file holds the Fertility rate (births per woman) and the female Life Expectancy at birth (in years) for 200 countries of the world. Response variable is: Life expec
> In Chapter 7, we There is found a relationship between the age of a bridge in Tompkins County, New York, and its condition as found by inspection. (Data in Tompkins County Bridges 2016) But we considered only bridges built or replaced since 1900. Tompkin
> Look again at the graph of the age at first marriage for women in Exercise 42. Here is a regression model for the data on women, along with a residuals plot: Response variable is: Women R-squared = 61.1% s = 1.474 1. Based on this model, what would you p
> In Exercise 46, we saw in the Swim the Lake 2016 data that Vicki Keith round-trip swim of Lake Ontario was an obvious outlier among the other one-way times. Here is the new regression after this unusual point is removed: Dependent variable is Time R-Squa
> The errors in predicting hurricane tracks (examined in this chapter) were given in nautical miles. A statutory mile is 0.86898 nautical mile. Most people living on the Gulf Coast of the United States would prefer to know the prediction errors in statutor
> We removed humans from the scatterplot of the Gestation data in Exercise 45 because our species was an outlier in life expectancy. The resulting scatterplot (below) shows two points that now may be of concern. The point in the upper right corner of this
> People swam across Lake Ontario from Niagara-on-the-Lake to Toronto (52 km, or about 32.3 mi) 62 times between 1954 and 2016. We might be interested in whether the swimmers are getting any faster or slower. Here are the regression of the crossing Times (
> For humans, pregnancy lasts about 280 days. In other species of animals, the length of time from conception to birth varies. Is there any evidence that the gestation period is related to the animal life span? The first scatterplot shows Gestation Period
> Has the trend of decreasing difference in age at first marriage seen in Exercise 42 gotten stronger recently? The scatterplot and residual plot for the data from 1980 through 2015, along with a regression for just those years, are below. 1. Is this linea
> In Exercise 41, you investigated the federal rate on 3-month Treasury bills between 1950 and 1980. The scatterplot below shows that the trend changed dramatically after 1980, so we computed a new regression model for the years 1981 to 2015. Here the mode
> The graph shows the ages of both men and women at first marriage (www.census.gov). Clearly, the patterns for men and women are similar. But are the two lines getting closer together? Here are a timeplot showing the difference in average age (menÃ&
> Here are a plot and regression output showing the federal rate on 3-month Treasury bills from 1950 to 1980, and a regression model fit to the relationship between the Rate (in %) and Years Since 1950 (www.gpoaccess.gov/eop/). 1. What is the correlation b
> How does the speed at which you drive affect your fuel economy? To find out, researchers drove a compact car for 200 miles at speeds ranging from 35 to 75 miles per hour. From their data, they created the model Fuel Efficiency=320.1 Speed and created thi
> After keeping track of his heating expenses for several winters, a homeowner believes he can estimate the monthly cost from the average daily Fahrenheit temperature by using the model Cost=133 2.13 Temp. Here is the residuals plot for his data: 1. Interp
> A college admissions officer, defending the college use of SAT scores in the admissions process, produced the following graph. It shows the mean GPAs for last year freshmen, grouped by SAT scores. How strong is the evidence that SAT Score is a good predi
> A researcher investigating the association between two variables collected some data and was surprised when he calculated the correlation. He had expected to find a fairly strong association, yet the correlation was near 0. Discouraged, he didn’t bother
> To measure progress in reading ability, students at an elementary school take a reading comprehension test every year. Scores are measured in grade-level units; that is, a score of 4.2 means that a student is reading at slightly above the expected level
> A researcher studying violent behavior in elementary school children asks the children parents how much time each child spends playing computer games and has their teachers rate each child on the level of aggressiveness they display while playing with ot
> Suppose a researcher studying health issues measures blood pressure and the percentage of body fat for several adult males and finds a strong positive association. Describe three different possible cause-and-effect relationships that might be present.
> The original five points in Exercise 33 produce a regression line with slope 0. Match each of the red points (ae) with the slope of the line after that one point is added: 1. 0.45 2. 0.30 3. 0.00 4. 0.05 5. 0.85
> The scatterplot shows five blue data points at the left. Not surprisingly, the correlation for these points is r=0. Suppose one additional data point is added at one of the five positions suggested below in red. Match each point (ae) with the correct new
> Each of the following scatterplots shows a cluster of points and one stray point. For each, answer these questions: 1. In what way is the point unusual? Does it have high leverage, a large residual, or both? 2. Do you think that point is an influential p
> Each of these four scatterplots shows a cluster of points and one stray point. For each, answer these questions: 1. In what way is the point unusual? Does it have high leverage, a large residual, or both? 2. Do you think that point is an influential poin
> In Chapter 6, we saw data on the errors (in nautical miles) made by the National Hurricane Center in predicting the path of hurricanes. The scatterplot below shows the trend in the 24-hour tracking errors since 1970 (www.nhc.noaa.gov). 1. Interpret the s
> The scatterplot below shows the number of passengers at Oakland (CA) airport month by month since 1997 (oaklandairport.com/news/statistics/passenger-history/). 1. Describe the patterns in passengers at Oakland airport that you see in this time plot. 2. U
> In Exercise 22, we examined the percentage of men aged 1824 who smoked from 1965 to 2014 according to the Centers for Disease Control and Prevention. How about women? Here a scatterplot showing the corresponding percentages for both men and women along w
> Is there an association between time of year and the nighttime temperature in North Dakota? A researcher assigned the numbers 1365 to the days January 1 December 31 and recorded the temperature at 2:00 A.M. for each. What might you expect the correlation
> Here a scatterplot of the production budgets (in millions of dollars) vs. the running time (in minutes) for major release movies in 2005. Dramas are plotted as red x and all other genres are plotted as blue dots. (The re-make of King Kong is plotted as a
> A student who has created a linear model is disappointed to find that her R2 value is a very low 13%. 1. Does this mean that a linear model is not appropriate? Explain. 2. Does this model allow the student to make accurate predictions? Explain.
> In justifying his choice of a model, a student wrote, know this is the correct model because R2=99.4%. 1. Is this reasoning correct? Explain. 2. Does this model allow the student to make accurate predictions? Explain.
> As explained in Exercise 23, the Human Development Index (HDI) is a measure that attempts to summarize in one number the progress in health, education, and economics of a country. The percentage of older people (65 and older) in a country is positively a
> The United Nations Development Programme (UNDP) uses the Human Development Index (HDI) in an attempt to summarize in one number the progress in health, education, and economics of a country (hdr.undp.org/en/data#). In 2015, the HDI was as high as 0.94 fo
> The Centers for Disease Control and Prevention tracks cigarette smoking in the United States (www.cdc.gov/nchs). How has the percentage of people who smoke changed since the danger became clear during the last half of the 20th century? The scatterplot sh
> Is there evidence that the age at which women get married has changed over the past 100 years? The scatterplot shows the trend in age at first marriage for American women (www.census.gov). 1. Is there a clear pattern? Describe the trend. 2. Is the associ
> The data file Receivers 2015 holds information about the 488 NFL players who caught at least one pass during the 2015 football season. A typical 53-man roster has about 13 players who would be expected to catch passes (primarily wide receivers, tight end
> Exercise 41 Chapter 6 looked at a sample of 35 vehicles to examine the relationship between gas mileage and engine displacement. The full dataset holds data on 1211 cars. How well did our sample of 35 represent the underlying relationship between displac
> Consider the four points (200,1950), (400,1650), (600,1800), and (800,1600). The least squares line is y^=1975+0.45x. Explain what least squares means, using these data as a specific example.
> Consider the four points (10,10), (20,50), (40,20), and (50,80). The least squares line is y=7.0+1.1x. Explain what least squares means, using these data as a specific example.
> Wildlife researchers monitor many wildlife populations by taking aerial photographs. Can they estimate the weights of alligators accurately from the air? Here is a regression analysis of the Weight of alligators (in pounds) and their Length (in inches) b
> In an investigation of environmental causes of disease, data were collected on the annual mortality rate (deaths per 100,000) for males in 61 large towns in England and Wales. In addition, the water hardness was recorded as the calcium concentration (par
> We saw the data for the women 2016 Olympic heptathlon in Exercise 73. Are the two jumping events associated? Perform a regression of the long-jump results on the high-jump results. 1. What is the regression equation? What does the slope mean? 2. What per
> We discussed the women 2016 Olympic heptathlon in Chapter 5. Here are the results from the high jump, 800-meter run, and long jump for the 27 women who successfully completed all three events of the heptathlon in the 2016 Olympics: Let examine the associ
> Would a model that uses the person Waist size be able to predict the %Body Fat more accurately than one that uses Weight? Using the data in Exercise 71, create and analyze that model.
> It is difficult to determine a person body fat percentage accurately without immersing him or her in water. Researchers hoping to find ways to make a good estimate immersed 20 male subjects, then measured their waists and recorded their weights shown in
> In Exercise 69, we saw the relationship between CO2 measured at Mauna Loa and average global temperature anomaly from 1959 to 2016. Here is a plot of average global temperatures plotted against the yearly final value of the Dow Jones Industrial Average f
> The earth climate is getting warmer. The most common theory attributes the increase to an increase in atmospheric levels of carbon dioxide (CO2), a greenhouse gas. Here is a scatterplot showing the mean annual temperature anomaly (the difference between
> The table shows the number of live births per 1000 population in the United States, starting in 1965. (National Center for Health Statistics, www.cdc.gov/nchs/) 1. Make a scatterplot and describe the general trend in Birthrates. (Enter Year as years sinc
> In a study of streams in the Adirondack Mountains, the following relationship was found between the water pH and its hardness (measured in grains): Is it appropriate to summarize the strength of association with a correlation? Explain. (Data in Streams)
> We saw in this chapter that in Tompkins County, New York, older bridges were in worse condition than newer ones. Tompkins is a rural area. Is this relationship true in New York City as well? Here are data on the Condition (as measured by the state Depart
> Numbeo.com lists the cost of living (COL) for 576 cities around the world. It reports the typical cost of a number of staples. Here are a scatterplot and regression relating the cost of a cappuccino to the cost of a third of a liter of water: 1. Using th
> In Exercise 63, you created a model that can estimate the number of Calories in a burger when the Fat content is known. 1. Explain why you cannot use that model to estimate the fat content of a burger with 600 calories. 2. Using an appropriate model, est
> Chicken sandwiches are often advertised as a healthier alternative to beef because many are lower in fat. Tests on 11 brands of fast-food chicken sandwiches produced the following summary statistics and scatterplot from a graphing calculator: 1. Do you t
> In Chapter 6, you examined We can examine the association between the amounts of Fat and Calories in fast-food hamburgers. Here are the data: 1. Create a scatterplot of Calories vs. Fat. 2. Interpret the value of R2 in this context. 3. Write the equation
> Burger King introduced a meat-free burger in 2002. The nutrition label for the 2014 BK Veggie burger (no mayo) is shown here: (Data in Burger King items) 1. Use the regression model created in this chapter, Fat=8.4+0.91 Protein to predict the fat content
> Use the advertised prices for Toyota Corollas given in Exercise 59 to create a linear model for the relationship between a car Age and its Price. 1. Find the equation of the regression line. 2. Explain the meaning of the slope of the line. 3. Explain the
> Chapter 6, Exercise 42 examines results of a survey A survey was conducted in the United States and 10 countries of Western Europe to determine the percentage of teenagers who had used marijuana and other drugs. Below is the scatterplot. Summary statisti
> Carmax.com lists numerous Toyota Corollas for sale within a 250 mile radius of Redlands, CA. The table lists the ages of the cars and the advertised prices. 1. Make a scatterplot for these data. 2. Describe the association between Age and Price of a used
> We saw in Exercise 57 that the number of fires was nearly constant. But has the damage they cause remained constant as well? Here a regression that examines the trend in Acres per Fire (in hundreds of thousands of acres) together with some supporting plo
> A study compared the effectiveness of several antidepressants by examining the experiments in which they had passed the FDA requirements. Each of those experiments compared the active drug with a placebo, an inert pill given to some of the subjects. In e
> The National Interagency Fire Center (www.nifc.gov) reports statistics about wildfires. Here an analysis of the number of wildfires between 1985 and 2015. 1. Is a linear model appropriate for these data? Explain. 2. Interpret the slope in this context. 3
> Based on the statistics for college freshmen given in Exercise 54, what SAT score would you predict for a freshmen who attained a first-semester GPA of 3.0?
> Suppose we wanted to use SAT math scores to estimate verbal scores based on the information in Exercise 53. 1. What is the correlation? 2. Write the equation of the line of regression predicting verbal scores from math scores. 3. In general, what would a
> Colleges use SAT scores in the admissions process because they believe these scores provide some insight into how a high school student will perform at the college level. Suppose the entering freshmen at a certain college have mean combined SAT Scores of
> The SAT is a test often used as part of an application to college. SAT scores are between 200 and 800, but have no units. Tests are given in both Math and Verbal areas. SAT-Math problems require the ability to read and understand the questions, but can a
> For the online clothing retailer discussed in the previous problem, the scatterplot of Total Yearly Purchases by Income looks like this: The correlation between Total Yearly Purchases and Income is 0.722. Summary statistics for the two variables are: 1.
> An online clothing retailer keeps track of its customers purchases. For those customers who signed up for the company credit card, the company also has information on the customer Age and Income. A random sample of 500 of these customers shows the follow
> In Chapter 6, Exercise 40, we saw Below is a plot of mortgages in the United States (in trillions of 2013 dollars) vs. the interest rate at various times over the past 25 years. The correlation is r=0.845. The mean mortgage amount is $8.207 T and the mea
> In Chapter 6, Exercise 39, We learned that the Office of Federal Housing Enterprise Oversight (OFHEO) collects data on various aspects of housing costs around the United States. Here a scatterplot (by state) of the Housing Cost Index (HCI) vs. the Median
> Refer again to the regression analysis for home average attendance and games won by baseball teams, seen in Exercise 44. 1. Write the equation of the regression line. 2. Estimate the Home Average Attendance for a team with 750 Runs. 3. Interpret the mean
> Most roller coasters get their speed by dropping down a steep initial incline, so it makes sense that the height of that drop might be related to the speed of the coaster. Here a scatterplot of top Speed and largest Drop for 118 roller coasters around th
> Take another look at the regression analysis of tar and nicotine content of the cigarettes in Exercise 43. 1. Write the equation of the regression line. 2. Estimate the Nicotine content of cigarettes with 4 milligrams of Tar. 3. Interpret the meaning of
> Consider again the regression of Home Average Attendance on Runs for the baseball teams examined in Exercise 44. 1. What is the correlation between Runs and Home Average Attendance? 2. What would you predict about the Home Average Attendance for a team t
> Consider again the regression of Nicotine content on Tar (both in milligrams) for the cigarettes examined in Exercise 43. 1. What is the correlation between Tar and Nicotine? 2. What would you predict about the average Nicotine content of cigarettes that
> In Chapter 6, Exercise 45 looked We can look at the relationship between the number of runs scored by American League baseball teams and the average attendance at their home games for the 2016 season. Here are the scatterplot, the residuals plot, and par
> Is the nicotine content of a cigarette related to the tar? A collection of data (in milligrams) on 816 cigarettes produced the scatterplot, residuals plot, and regression analysis shown: 1. Do you think a linear model is appropriate here? Explain. 2. Exp
> Consider the roller coasters (with the outlier removed) described in Exercise 30 again. The regression analysis gives the model Duration=87.22+0.389 Drop. 1. Explain what the slope of the line says about how long a roller coaster ride may last and the he
> Consider the Albuquerque home sales from Exercise 29 again. The regression analysis gives the model Price=47.82+0.061Â Size. 1. Explain what the slope of the line says about housing prices and house size. 2. What price would you predict for a 3000-square
> Players in any sport who are having great seasons, turning in performances that are much better than anyone might have anticipated, often are pictured on the cover of Sports Illustrated. Frequently, their performances then falter somewhat, leading some a
> People who claim to have extrasensory perception (ESP) participate in a screening test in which they have to guess which of several images someone is thinking of. You and a friend both took the test. You scored 2 standard deviations above the mean, and y
> The regression of Duration of a roller coaster ride on the height of its initial Drop, described in Exercise 30, had R2=29.4%. 1. What is the correlation between Drop and Duration? 2. What would you predict about the Duration of the ride on a coaster who
> The National Insurance Crime Bureau reports that Honda Accords, Honda Civics, and Toyota Camrys are the cars most frequently reported stolen, while Ford Tauruses, Pontiac Vibes, and Buick LeSabres are stolen least often. Is it reasonable to say that ther
> The regression of Price on Size of homes in Albuquerque had R2=71.4% as described in Exercise 29. 1. What is the correlation between Size and Price? 2. What would you predict about the Price of a home 1 SD above average in Size? 3. What would you predict
> A sociology student investigated the association between a country Literacy Rate and Life Expectancy, and then drew the conclusions listed below. Explain why each statement is incorrect. (Assume that all the calculations were done properly.) 1. The R2 of
> A biology student who created a regression model to use a bird Height when perched for predicting its Wingspan made these two statements. Assuming the calculations were done correctly, explain what is wrong with each interpretation. 1. My R2 of 93% shows
> Exercise 30 examined the association between the Duration of a roller coaster ride and the height of its initial Drop, reporting that R2=29.4%. Write a sentence (in context, of course) summarizing what the R2 says about this regression.
> The regression of Price on Size of homes in Albuquerque had R2=71.4%, as described in Exercise 29. Write a sentence (in context, of course) summarizing what the R2 says about this regression.
> If you create a regression model for estimating the Height of a pine tree (in feet) based on the Circumference of its trunk (in inches), is the slope most likely to be 0.1, 1, 10, or 100? Explain.
> If you create a regression model for predicting the Weight of a car (in pounds) from its Length (in feet), is the slope most likely to be 3, 30, 300, or 3000? Explain.

