Question: A survey of 156 introductory statistics students
A survey of 156 introductory statistics students showed the following contingency table. Find each event probability.
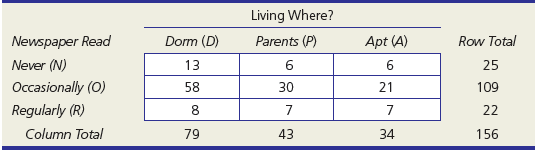
a. P(D)
b. P(R)
c. P(D > R)
d. P(D ∪ R)
e. P(R | D)
f. P(R | P)
Transcribed Image Text:
Living Where? Newspaper Read Dorm (D) Parents (P) Apt (A) Row Total Never (N) 13 6 6 25 Occasionally (0) 58 30 21 109 Regularly (R) 8. 7 7. 22 Column Total 79 43 34 156
> A foreclosure case saw creditors going after the business’s real estate. The business was a diner. However, the diner itself was a prefabricated building. The business owner claimed that the building itself was not realty and subject to the creditors’ cl
> Consider the status of being a merchant under the UCC. Should the UCC differentiate between merchants and nonmerchants?
> Explain what determines whether a contract is covered by the UCC.
> Brad Gupta formed two companies, Ameriquest Holdings and Ananya Aviation, for which he purchased three airplanes that were in lease agreements with US Airways and Continental Airlines. However, after the events of September 11, 2001, the two airlines did
> The opera company was hired to perform in the outside pavilion of the Wolf Trap Foundation. The company performed the three performances without problem. Then, right before the last performance, a severe thunderstorm moved into the area and created an el
> In 1991, EnerSys entered into an agreement with Exide Technologies to purchase substantially all of Exide’s battery business for about $135 million. To formalize this sale, the parties entered into more than 23 agreements. Under the collection of agreeme
> Jarold Daniel Friedman worked as a temporary computer contractor for a pharmaceutical warehouse. The warehouse offered him a permanent position, but the warehouse required him to get a mumps vaccine, grown in chicken embryos, as a condition of his perman
> What ethical guidelines could help an American business manager working in another country decide whether she should engage in behavior that is ethical where she works but unethical in the United States?
> Refer to the data in Exercise 1 for Weller Corporation. Comparative financial statements for Weller Corporation, a merchandising company, for the year ending December 31 appear below. The company did not issue any new common stock during the year. A tot
> Refer to the financial statements for Castile Products, Inc., in Exercise 15–8. In addition to the data in these statements, assume that Castile Products, Inc., paid dividends of $2.10 per share during the year. Also assume that the company’s common stoc
> Refer to the data in Exercise 1 for Weller Corporation. Data given in Exercise 1: Comparative financial statements for Weller Corporation, a merchandising company, for the year ending December 31 appear below. The company did not issue any new common st
> Refer to the data in Exercise 1 for Weller Corporation. Data given in Exercise 1: Comparative financial statements for Weller Corporation, a merchandising company, for the year ending December 31 appear below. The company did not issue any new common st
> Shimada Products Corporation of Japan is anxious to enter the electronic calculator market. Management believes that in order to be competitive in world markets, the price of the electronic calculator that the company is developing cannot exceed $15. Shi
> Refer to the data in Exercise 1 for Weller Corporation. Comparative financial statements for Weller Corporation, a merchandising company, for the year ending December 31 appear below. The company did not issue any new common stock during the year. A tot
> Comparative financial statements for Weller Corporation, a merchandising company, for the year ending December 31 appear below. The company did not issue any new common stock during the year. A total of 800,000 shares of common stock were outstanding. Th
> Martin Company uses the absorption costing approach to cost-plus pricing.It is considering the introduction of a new product. To determine a selling price, the company has gathered the following information: Number of units to be produced and sold each
> What type of data (categorical, discrete numerical, or continuous numerical) is each of the following variables? If there is any ambiguity about the data type, explain why the answer is unclear. a. The miles on your car’s odometer. b. The fat grams you a
> What type of data (categorical, discrete numerical, or continuous numerical) is each of the following variables? If there is any ambiguity, explain why the answer is unclear. a. Length of a TV commercial. b. Number of peanuts in a can of Planter’s Mixed
> What type of data (categorical, discrete numerical, or continuous numerical) is each of the following variables? If there is any ambiguity about the data type, explain why the answer is unclear. a. The manufacturer of your car. b. Your college major. c.
> The manufacturer of Glo-More flat white interior latex paint claims one-coat coverage of 400 square feet per gallon on interior walls. A painter keeps careful track of 6 gallons and finds coverage (in square feet) of 360, 410, 380, 360, 390, 400. (a) At
> Calculate the test statistic and p-value for each sample. State the conclusion for the specified α. а. Но: 3 200 versus H: p # 200, a %3D.025, х%3D 203, s 3D 8, п %3D 16 b. Hg: μ 200 versus H: μ < 200, α -05, Σ= 198 , s 5, n = 25 с. Но
> Estimate the p-value as a range using Appendix D (not Excel): Appendix D: a. t = 1.457, d.f. = 14, right-tailed test b. t = 2.601, d.f. = 8, two-tailed test c. t = 21.847, d.f. = 22, left-tailed test Confidence Level Confidence Level .80 .90 .95 .
> A firm decides to test its employees for illegal drugs. (a) State the null and alternative hypotheses. (b) Define Type I and II errors. (c) What are the consequences of each type of error, and to whom?
> The target activation force of the buttons on a keyless entry clicker is 1.967 newtons. Variation exists in activation force due to the nature of the manufacturing process. A sample of 9 clickers showed a mean activation force of 1.88 newtons. The standa
> Discuss the issues of statistical significance and practical importance in each scenario. a. A process for producing I-beams of oriented strand board used as main support beams in new houses has a mean breaking strength of 2,000 lbs./ft. A sample of boar
> The Scottsdale fire department aims to respond to fire calls in 4 minutes or less, on average. Response times are normally distributed with a standard deviation of 1 minute. Would a sample of 18 fire calls with a mean response time of 4 minutes 30 second
> On the midnight shift, the number of patients with head trauma in an emergency room has the probability distribution shown below. (a) Find P(X > 3). (b) Find P(X < 2). (c) Find P(X < 4). (d) Find P(X = 1). (e) Which of the probability expressions in part
> An airline serves bottles of Galena Spring Water that are supposed to contain an average of 10 ounces. The filling process follows a normal distribution with process standard deviation 0.07 ounce. Twelve randomly chosen bottles had the weights shown belo
> The mean arrival rate of flights at O’Hare Airport in marginal weather is 195 flights per hour with a historical standard deviation of 13 flights. To increase arrivals, a new air traffic control procedure is implemented. In the next 30
> Define Type I and Type II error for each scenario, and identify the cost(s) of each type of error. a. A 25-year-old ER patient in Minneapolis complains of chest pain. Heart attacks in 25-year olds are rare, and beds are scarce in the hospital. The null
> Calculate the test statistic and p-value for each sample. a. H0: μ = 60 versus H1: μ ≠ 60, α = .025, / = 63, σ = 8, n = 16 b. H0: μ > 60 versus H1: μ < 60, α = .05, / = 58, σ = 5, n = 25 c. H0: μ < 60 versus H1: μ > 60, α = .05, / = 65, σ = 8, n = 36
> The mean potassium content of a popular sports drink is listed as 140 mg in a 32-oz bottle. Analysis of 20 bottles indicates a sample mean of 139.4 mg. (a) Write the hypotheses for a two-tailed test of the claimed potassium content. (B) Assuming a known
> How large a sample size would be needed to estimate the percentage of wireless routers in San Francisco that use data encryption, with an error of ±2 percent and 95 percent confidence?
> What sample size would be needed to estimate the true proportion of students at your college (if you are a student) who are wearing backpacks, with 95 percent confidence and an error of ±0.04?
> What sample size would be required to estimate the true proportion of American female business executives who prefer the title “Ms.,” with an error of ±0.025 and 98 percent confidence?
> The EPA city/hwy mpg range for a Saturn Vue FWD automatic 5-speed transmission is 20 to 28 mpg. (a) Estimate σ using Method 3 from Table 8.11. (b) If you owned this vehicle, how large a sample (e.g., how many tanks of gas) would be required to
> For each level of precision, find the required sample size to estimate the mean starting salary for a new CPA with 95 percent confidence, assuming a population standard deviation of $7,500 (same as last year). a. E = $2,000 b. E = $1,000 c. E = $500
> Police records in the town of Saratoga show that 15 percent of the drivers stopped for speeding have invalid licenses. If 12 drivers are stopped for speeding, find the probability that (a) none will have an invalid license; (b) exactly one will have an i
> Use the following information x bar = 3.7, s = 0.2, n = 1,200, N = 5,800—to calculate confidence intervals for μ assuming the sample is from a normal population: (a) 90 percent confidence; (b) 95 percent confidence; (c) 99 percent confidence.
> Concerns about climate change and CO2 reduction have initiated the commercial production of blends of biodiesel (e.g., from renewable sources) and petrodiesel (from fossil fuel). Random samples of 35 blended fuels are tested in a lab to ascertain the bio
> Calculate the FPCF for each sample and population size. Can the population be considered effectively infinite in each case? a. N = 450, n = 10 b. N = 300, n = 25 c. N = 1800, n = 280
> A real estate office has 10 sales agents. Each of four new customers must be assigned an agent. (a) Find the number of agent arrangements where order is important. (b) Find the number of agent arrangements where order is not important. (c) Why is the num
> At Oxnard University, a student ID consists of two letters (26 possibilities) followed by four digits (10 possibilities). (a) How many unique student IDs can be created? (b) Would one letter followed by three digits suffice for a university with 40,000 s
> In the Minnesota Northstar Cash Drawing you pick five different numbers between 1 and 31. What is the probability of picking the winning combination (order does not matter)? Hint: Count how many ways you could pick the first number, the second number, an
> An airport gamma ray luggage scanner coupled with a neural net artificial intelligence program can detect a weapon in suitcases with a false positive rate of 2 percent and a false negative rate of 2 percent. Assume a .001 probability that a suitcase cont
> A drug test for athletes has a 5 percent false positive rate and a 10 percent false negative rate. Of the athletes tested, 4 percent have actually been using the prohibited drug. If an athlete tests positive, what is the probability that the athlete has
> The following contingency table shows average yield (rows) and average duration (columns) for 38 bond funds. For a randomly chosen bond fund, find the probability that: a. The bond fund is long duration. b. The bond fund has high yield. c. The bond fun
> The diameter of bushings turned out by a manufacturing process is a normally distributed random variable with a mean of 4.035 mm and a standard deviation of 0.005 mm. A sample of 25 bushings is taken once an hour. (a) Within what interval should 95 perce
> This contingency table describes 200 business students. Find each probability and interpret it in words. a. P(A) b. P(M) c. P(A > M) d. P(F > S) e. P(A | M) f. P(A | F) g. P(F | S) h. P(E ∪ F) Major Gender Accounting (
> A survey of 158 introductory statistics students showed the following contingency table. Find each event probability. a. P(V) b. P(A) c. P(A > V) d. P(A ∪ V) e. P(A | V) f. P(V | A) Cell Phone Provider Visa Card (V) No Visa
> The contingency table below shows the results of a survey of online video viewing by age. Find the following probabilities or percentages: a. Probability that a viewer is aged 18–34. b. Probability that a viewer prefers watching TV vi
> Over 1,000 people try to climb Mt. Everest every year. Of those who try to climb Everest, 31 percent succeed. The probability that a climber is at least 60 years old is .04. The probability that a climber is at least 60 years old and succeeds in climbing
> Bob sets two alarm clocks (battery-powered) to be sure he arises for his Monday 8:00 a.m. accounting exam. There is a 75 percent chance that either clock will wake Bob. (a) What is the probability that Bob will oversleep? (b) If Bob had three clocks, wou
> Which pairs of events are independent? a. P(J ) = .50, P(K) = .40, P(J ∩ K ) = .3. b. P(J ) = .60, P(K) = .20, P(J ∩ K ) = .12. c. P(J ) = .15, P(K) = .5, P(J ∩ K ) = .1.
> Given P(J) = .2, P(K) = .4 and P(J ∩ K) = .15. (a) Find P(J | K). (b) In this problem, are J and K independent?
> Which pairs of events are independent? a. P(A) = .60, P(B) = .40, P(A ∩ B) = .24. b. P(A) = .90, P(B) = .20, P(A ∩ B) = .18. c. P(A) = .50, P(B) = .70, P(A ∩ B) = .25.
> Let C be the event that a randomly chosen adult has some college education. Let M be the event that a randomly chosen adult is married. Given P(C) = .4, P(M) = .5 and P(C ∩ M) = .24, find each probability. a. P(C9). b. P(C ∪ M). c. P(M | C). d. P(C | M).
> Prof. Green gave three exams last semester. Scores were normally distributed on each exam. Below are scores for 10 randomly chosen students on each exam. (a) Find the 95 percent confidence interval for the mean score on each exam. (b) Do the confidence i
> Let S be the event that a randomly chosen female aged 18–24 is a smoker. Let C be the event that a randomly chosen female aged 18–24 is a Caucasian. Given P(S) = .246, P(C) = .830, and P(S ∩ C) = .232, find each probability. a. P(S9). b. P(S ∪ C). c. P(S
> Are these events collectively exhaustive or not? Explain. a. A 5 college grad, B 5 some college, C 5 no college b. A 5 born in the United States, B 5 born in Canada, C 5 born in Mexico c. A 5 full-time student, B 5 part-time student, C 5 not enrolled as
> Are these characteristics of a student at your university mutually exclusive or not? Explain. a. A 5 works 20 hours or more, B 5 majoring in accounting b. A 5 born in the United States, B 5 born in Canada c. A 5 owns a Toyota, B 5 owns a Honda
> CitiBank recorded the number of customers to use a downtown ATM during the noon hour on 32 consecutive workdays. (a) Find the mean, median, and mode. (b) Do these measures of center agree? Explain. (c) Make a histogram or dot plot. (d) Are the data symme
> Prof. Hardtack gave four Friday quizzes last semester in his 10-student senior tax accounting class. (a) Find the mean, median, and mode for each quiz. (b) Do these measures of center agree? Explain. (c) For each data set, note strengths or weaknesses of
> Scores are shown for the most recent state civil service exam taken by 24 applicants for positions in law enforcement. (a) Calculate the mean, median, and mode. (b) Is the distribution skewed? Explain. (c) Is the mode a useful measure of center for this
> Days on the market are shown for the 36 most recent home sales in the city of Sonando Hills. (a) Calculate the mean, median, and mode. (b) Is the distribution skewed? Explain. (c) Is the mode a useful measure of center for this data set? 18 70 52 17
> For each data set, which best indicates a “typical” data value (mean, median, either)? a. MPG for 7 Honda Civics: 21.8, 24.1, 24.6, 26.2, 28.4, 35.2, 36.3 b. Number of riders in 8 cars: 1, 1, 1, 1, 1, 1, 4, 6 c. D
> For each data set, which best indicates a “typical” data value (mean, median, either)? a. Days on campus by 11 students: 1, 1, 2, 2, 3, 3, 3, 4, 4, 5, 5 b. P/E ratios of 6 stocks: 1.5, 6.5, 6.6, 7.3, 8.2, 9.1 c. Textbooks in 9 backpacks: 0, 0, 0, 0, 0,
> The mean collection period for accounts receivable at Ephemeral Products is 18.5 days with a standard deviation of 4.8 days. (a) What is the standardized z-score for an account that is paid in 30 days? (b) Is that account an outlier? (c) How many days (t
> A random sample of 16 pharmacy customers showed the waiting times below (in minutes). Find a 90 percent confidence interval for μ, assuming that the sample is from a normal population. 21 22 22 17 21 17 23 20 20 24 9 22 16 21 22 21
> The mean monthly rent of students at Oxnard University is $875 with a standard deviation of $219. (a) John’s rent is $1,325. What is his standardized z-score? (b) Is John’s rent an outlier? (c) How high would the rent have to be to qualify as an outlier?
> For each data set, is the mode a good measure of center? Explain. a. GMAT scores (8 MBA applicants): 490, 495, 542, 587, 599, 622, 630, 641 b. Exam grades (12 students): F, D, C, C, C, C, C, C, B, B, A, A c. Body Mass Index (7 Army recruits): 18.6, 20.2
> Prof. Hardtack gave four Friday quizzes last semester in his senior tax accounting class. A random sample of 10 student scores is shown for each quiz. (a) Find the sample mean, standard deviation, and coefficient of variation for each quiz. (b) How do th
> (a) Find the coefficient of variation for prices of these three stocks. (b) Which stock has the greatest relative variation? (c) To measure variability, why not just compare the standard deviations? Stock A: X = $24.50, s = 5.25 Stock B: x= $147.25,
> For each data set: (a) Find the mean. (b) Find the standard deviation, treating the data as a sample. (c) Find the standard deviation, treating the data as a population. (d) What does this exercise show about the two formulas? Data Set A: 6, 7, 8 Data Se
> (a) Find the mean and standard deviation for each sample. (b) What does this exercise show about the standard deviation? Sample A: 6, 7, 8 Sample B: 61, 62, 63 Sample C: 1,000, 1,001, 1,002
> Estimate the mean from the following table of grouped data and frequencies. From То 2 6. 7 6. 10 12 10 14 3 14 18 2 18 22 1 Total 25 ν ν ν ν ν
> Estimate the mean from this table of grouped data and frequencies: From То 20 20 40 12 40 60 18 60 80 9 Total 44 v v v v
> For each data set, is the mode a good measure of center? Explain. a. Genders of 12 CEOS: М, М, F, M, F, М, М, М, F, M, M, М b. Ages of 10 college freshmen: c. Ages of 8 MBA students: 17, 17, 18, 18, 18, 18, 18, 18, 19, 20 24, 26, 27, 28, 30, 31, 33,
> For a sample of (X, Y) data values, the covariance is 48.724, the standard deviation of X is 11.724, and the standard deviation of Y is 8.244. (a) Find the sample correlation coefficient. (b) What does the sample correlation coefficient suggest about the
> A random sample of 25 items is drawn from a population whose standard deviation is unknown. The sample mean is x bar = 850 and the sample standard deviation is s = 15. Use Appendix D to find the values of Student’s t. a. Construct an interval estimate o
> Spirit Airlines kept track of the number of empty seats on flight 308 (DEN–DTW) for 10 consecutive trips on each weekday except Friday. (a) Sort the data for each day. (b) Find the mean, median, mode, midrange, geometric mean, and 10 percent trimmed mean
> For each X-Y data set (n 5 12): (a) Make a scatter plot. (b) Find the sample correlation coefficient. (c) Is there a linear relationship between X and Y? If so, describe it. Note: Use Excel or MegaStat or MINITAB if your instructor permits. Data Set
> An executive’s telephone log showed the lengths of 65 calls initiated during the last week of July. (a) Use Excel to find the quartiles. What do they tell you? (b) Find the midhinge. What does it tell you? (c) Make a box plot and interp
> CitiBank recorded the number of customers to use a downtown ATM during the noon hour on 32 consecutive workdays. (a) Use Excel to find the quartiles. What do they tell you? (b) Find the midhinge. What does it tell you? (c) Make a box plot and interpret i
> The city of Sonando Hills has 8 police officers. In January, the work-related medical expenses for each officer were 0, 0, 0, 0, 0, 0, 150, 650. (a) Calculate the mean, median, mode, midrange, and geometric mean. (b) Which measure of center would you use
> The Comer-Correr Taco Wagon is only open from 11:00 a.m. to 2:00 p.m. on Saturday. The owner kept track of the number of customers served on Saturday for 60 weeks. (a) Visually estimate the quartiles Q1, Q2, Q3. (b) Approximately how many customers were
> In the Excel function = TRIMMEAN(Data,.10), how many observations would be trimmed from each end of the sorted data array named Data if (a) n = 41, (b) n = 66, and (c) = 83?
> (a) For each data set, find the median, midrange, and geometric mean. (b) Are they reasonable measures of central tendency? Explain. a. Exam scores (9 students) b. GPAS (8 students) c. Class absences (12 students) 42, 55, 65, 67, 68, 75, 76, 78, 94
> On Friday night, the owner of Chez Pierre in downtown Chicago noted the amount spent for dinner for 28 four-person tables. (a) Find the mean, median, and mode. (b) Do these measures of center agree? Explain. (c) Make a histogram or dot plot. (d) Are the
> (a) For each data set, find the mean, median, and mode. (b) Discuss anything about the data that affects the usefulness of each statistic as a measure of center. 0, 0, 0, 0, 0, 1, 2, 3, 3, 5, 5, 15 a. Class absences (12 students): b. Exam scores (9
> A random sample of 10 items is drawn from a population whose standard deviation is unknown. The sample mean is xbar = 270 and the sample standard deviation is s = 20. Use Appendix D to find the values of Student’s t. a. Construct an interval estimate for
> An executive’s telephone log showed the lengths of 65 calls initiated during the last week of July. (a) Use Excel or MegaStat to sort and standardize the data. (b) Based on the standardized z scores, are there outliers? Unusual data val
> CitiBank recorded the number of customers to use a downtown ATM during the noon hour on 32 consecutive workdays. (a) Use Excel or MegaStat to sort and standardize the data. (b) Based on the Empirical Rule, are there outliers? Unusual data values? (c) Com
> Find the original data value corresponding to each standardized z-score. a. Student GPAs: Bob's z-score b. Weekly work hours: Sarah's z-score c. Bowling scores: Dave's z-score z = +1.71, µ = 2.98, ở = 0.36 z+118 , μ = 21.6, σ = 7.1 z-1.35, μ = 150,
> In a regional high school swim meet, women’s times (in seconds) in the 200-yard freestyle ranged from 109.7 to 126.2. Estimate the standard deviation, using the Empirical Rule.
> Convert each individual X data value to a standardized Z value and interpret it. a. Class exam: b. Student GPA: c. Weekly study hours: John's scor is 91,μ = 79, σ5 Mary's GPA is 3.18, µ = 2.87, o = 0.31 Jaime studies 18 hours, u = 15.0, o = 5.0
> Convert each individual data value to a standardized z-score. Is it an outlier? a. Ages of airline passengers: x = 92, μ = 46, σ = 13 b. Accounting exam scores: x = 70, μ = 81, σ = 6 c. Condo rental vacancy days: x = 28, μ = 22, σ = 7
> For each frequency distribution, suggest “nice” bins. Did your choice agree with Sturges’ Rule? If not, explain. a. Last week’s MPG for 35 student vehicles (xmin = 9.4, xmax = 38.7). b. Ages of 50 airplane passengers (xmin = 12, xmax = 85). c. GPAs of 2
> (a) Make a frequency distribution and histogram for the 2007 annual compensation of 40 randomly chosen CEOs (millions of dollars). (b) Describe the shape of the histogram. (c) Identify any unusual values. (Source: www.forbes.com.) 5.33 18.3 24.55 9.
> (a) Make a frequency distribution and histogram for the monthly off-campus rent paid by 30 students. (b) Repeat the exercise, using a different number of bins. Which is preferred? Why? 730 730 730 930 700 570 690 1,030 740 620 720 670 560 740 650 66

