[SOLVED]

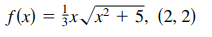
> Use the information in Exercise 2-25 to prepare a December statement of retained earnings for Help Today. The Retained Earnings account balance at December 1 was $0. Hint: Net income for December is $10,470.

> Create a table similar to Exhibit 1.9. Then use additions and subtractions to show the dollar effects of each transaction on individual items of the accounting equation. a. The company completed consulting work for a client and immediately collected $5,5

> Determine whether each of the following transactions increases or decreases equity. a. Owner invested cash in the company. b. Incurred maintenance expenses. c. Performed services for a client. d. Incurred employee wage expenses.

> Prepare Riley Company’s journal entries to record the following transactions for the current year. Apr. 18 Purchases 300 common shares of XLT Co. as a short-term investment at a cost of $42 per share. With this stock investment, Riley has an insignific

> Identify the accounting principle or assumption that best explains each situation. 1. In December of this year, Chavez Landscaping received a customer’s order and cash prepayment to install sod at a house that would not be ready for installation until Ma

> Teamwork is important in today’s business world. Successful teams schedule convenient meetings, maintain regular communications, and cooperate with and support their members. This assignment aims to establish support/learning teams, initiate discussions,

> Visit the EDGAR database at sec.gov/edgar/searchedgar/companysearch.html. Access the Form 10-K report of Rocky Mountain Chocolate Factory (ticker: RMCF) filed on May 15, 2018, covering its 2018 fiscal year. Required 1. Item 6 of the 10-K report provides

> Access the SEC EDGAR database (sec.gov/edgar) and retrieve Apple’s 2018 10-K (filed November 5, 2018). Identify its auditor. What responsibility does its independent auditor claim regarding Apple’s financial statements?

> Refer to Google’s financial statements in GOOGLE Appendix A near the end of the text. To what level of significance are dollar amounts rounded? What time period does their income statements cover?

> Key comparative figures for both Apple and Google follow. Required 1. What is the total amount of assets invested for the current year in (a) Apple and (b) Google? 2. What is the current-year return on assets for (a) Apple and (b) Google? 3. How much

> Key financial figures for Appleâs two most recent fiscal years follow. Required 1. What is the total amount of assets invested in Apple in the current year? 2. What is Appleâs return on assets for the current year? 3.

> On October 1, 2020, Santana Rey launched a computer services company, Business Solutions that is organized as a corporation and provides consulting services, computer system installations, and custom program development. Required Create a table like Exhi

> Use the information in Problem 1-3B to prepare the current year-end balance sheet for Audi Company.

> Refer to the information in QS C-9. (1) After the fair value adjustment is made, prepare the assets section of Reggit Company’s December 31 classified balance sheet. (2) Is the unrealized gain (or loss) on the portfolio of available-for-sale securities r

> Which of the following statements are true of long-term investments? a. They can be considered cash equivalents. b. They can include assets not used in operations, such as investments in land. c. They generally include investments that will mature in 3 t

> Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results. Function: y = (4x + 1)2 Point: (0, 1)

> Determine the point(s) in the interval (0, 2Ï) at which the graph of horizontal tangent.

> (a)Find an equation of the tangent line to the graph of the function at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results.

> Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results.

> Find the derivative of the trigonometric function.

> The slope of the function Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false.

> The graphs of f and g are shown. Let h(x) = f (g(x)) and s(x) = g( f (x)). Find each derivative, if it exists. If the derivative does not exist, explain why. Find hâ (1) Find sâ (5)

> Given that g(5) = â3, gâ²(5) = 6, h(5) = 3, and hâ²(5) = â2, find fâ²(5) for each of the following, if possible. If it is not possible, state what additional informati

> The table shows some values of the derivative of an unknown function f. Complete the table by finding the derivative of each transformation of f, if possible. g(x) = f(x) â 2 h(x) = 2 f(x) r(x) = f(-3x) s(x) = f(x + 2)

> Consider the function In general, how do you find the derivative of composite function? Find râ²(x) using the Product Rule. Find râ²(x) using the Quotient Rule. Which method do you prefer? Explain.

> Describe the relationship between f′ and g′. g(x) = f(3x) g(x) = f(x2 )

> The graphs of a function f and its derivative fâ² are shown. Label the graphs as f or fâ² and write a short paragraph stating the criteria you used in making your selection.

> Evaluate the second derivative of the function at the given point. Use a computer algebra system to verify your result.

> y = (2x - 7)3 Find the derivative of the function.

> Evaluate the second derivative of the function at the given point. Use a computer algebra system to verify your result.

> f(x) = sec2 πx Find the second derivative of the function.

> Find the second derivative of the function.

> f(x) = 6(x3 + 4)3 Find the second derivative of the function.

> f(x) = 5(2 – 7x)4 Find the second derivative of the function.

> Determine the point(s) at which the graph of has a horizontal tangent.

> Find an equation of the tangent line to the graph at the given point. Then use a graphing utility to graph the function and its tangent line at the point in the same viewing window. Bullet-nose curve

> Complete the table.

> Find an equation of the tangent line to the graph at the given point. Then use a graphing utility to graph the function and its tangent line at the point in the same viewing window. Semicircle

> (a)Find an equation of the tangent line to the graph of the function at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results.

> y = (4x3 + 3)2, (-1, 1) (a)Find an equation of the tangent line to the graph of the function at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility t

> (a)Find an equation of the tangent line to the graph of the function at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results.

> Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results.

> Complete the table.

> Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results.

> Find the slope of the tangent line to the sine function at the origin. Compare this value with the number of complete cycles in the interval [0, 2Ï].

> Use a computer algebra system to find the derivative of the function. Then use the utility to graph the function and its derivative on the same set of coordinate axes. Describe the behavior of the function that corresponds to any zeros of the graph of th

> Complete the table.

> Use a computer algebra system to find the derivative of the function. Then use the utility to graph the function and its derivative on the same set of coordinate axes. Describe the behavior of the function that corresponds to any zeros of the graph of th

> Find the derivative of the trigonometric function.

> y = 5 cos (πt ) 2 Find the derivative of the trigonometric function.

> Complete the table.

> f(t) = 3 sec (πt−1 ) 2 Find the derivative of the trigonometric function.

> Find the derivative of the trigonometric function.

> g(t) = 5 cos 2 πt Find the derivative of the trigonometric function.

> y = 4 sec2 x Find the derivative of the trigonometric function.

> Find the derivative of the trigonometric function.

> y = csc (1 – 2x)2 Find the derivative of the trigonometric function.

> Complete the table.

> Find the derivative of the trigonometric function.

> Find the derivative of the trigonometric function. y = cos 4x

> Find the derivative of the function. g(x) – (2 + (x2 + 1)4)3

> Find the derivative of the function. f(x) = ((x2 + 3)5 + x)2

> Find the derivative of the function.

> Find all differentiable functions f : RâR such that for all real numbers x and all positive integers n

> Prove that d/dx [cos x] = -Sin x.

> Where are the functions f1(x) = ∣sin x∣ and f2(x) = sin ∣x∣ differentiable?

> Find a and b such that f is differentiable everywhere.

> Find the equation(s) of the tangent line(s) to the graph of the parabola y = x2 through the given point not on the graph. (a) (0, a) (b) (a, 0) Are there any restrictions on the constant a?

> Find the equation(s) of the tangent line(s) to the graph of the curve y = x3 − 9x through the point (1, −9) not on the graph.

> Let (a, b) be an arbitrary point on the graph of y = 1/x, x > 0. Prove that the area of the triangle formed by the tangent line through (a, b) and the coordinate axes is 2.

> Find an equation of the parabola y = ax2 + bx + c that passes through (0, 1) and is tangent to the line y = x − 1 at (1, 0).

> Find the derivative of the function.

Question: