Question: After feeding a special diet to 80
After feeding a special diet to 80 mice, the scientist measures their weight in grams and obtains x = 35 grams and s = 4 grams. He states that a 90% confidence interval for µ is given by
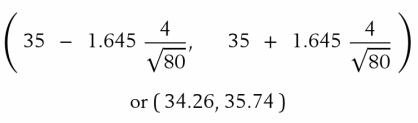
(a) Was the confidence interval calculated correctly? If not, provide the correct result.
(b) Does the interval (34.26, 35.74) cover the true mean? Explain your answer.
> A backpacking party carries three emergency signal flares, each of which lights with a probability of .94. Assuming that the flares operate independently, find: (a) The probability that at least one flare lights. (b) The probability that exactly two fl
> A market researcher intends to study the consumer preference between regular and decaffeinated coffee. Examine the plausibility of the model of Bernoulli trials in the following situations. (a) One hundred consumers are randomly selected and each is ask
> Refer to Exercise 5.45. Now suppose for each plot a fair coin is tossed. If a head shows up, the plot is treated; otherwise, it is a control. With this manner of treatment allocation, answer parts (a) and (b). Data from Exercise 5.45: From four agricult
> From four agricultural plots, two are selected at random for a pesticide treatment. The other two plots serve as controls. For each plot, denote by S the event that it is treated with the pesticide. Consider the assignment of treatment or control to a si
> Refer to Exercise 5.43 but instead assume that the jar contains 2000 pieces of wrapped hard candies, of which 700 are raspberry, 1000 are butterscotch , and 300 are other flavors. Repeat parts (a)-(c) of Exercise 5.43 in this setting. Data from Exercise
> A jar contains 20 pieces of wrapped hard candies, 7 are raspberry, 10 are butterscotch, and 3 are other flavors. Consider 4 successive draws of 1 piece of candy taken at random from the jar. Suppose the selection of butterscotch is the event of interest.
> In each case, examine whether or not repetitions of the stated experiment conform to the model of Bernoulli trials. Where the model is appropriate, determine the numerical value of p or indicate how it can be determined. (a) Roll a fair die and observe
> Is the model of Bernoulli trials plausible in each of the following situations? Discuss in what manner (if any) a serious violation of the assumptions can occur. (a) Seven friends go to a blockbuster movie and each is asked whether the movie was excellen
> Given the two probability distributions (a) Construct probability histograms. Which distribution has a larger spread? (b) Verify that both distributions have the same mean. (c) Compare the two standard deviations.
> Definition: The median of a distribution is the value m0 of the random variable such that P [X ≤ m0] ≥ .5 and P [X ≥ m0] ≥ .5 . In other words, the probability at or below m0 is at le
> Given here are the probability distributions of two random variables X and Y. (a) From the X distribution, determine the distribution of the random variable 8 - 2X and verify that it coincides with the Y distribution. (b) Calculate the mean and standard
> Determine a 99% confidence interval for µ using the data in Exercise 9.49. Data from Exercise 9.49: Measurements of the amount of suspended solids in river water on 14 Monday mornings yield x = 47 and s = 9 .4 mg/I. Obtain a 95% confidence interval for
> Measurements of the amount of suspended solids in river water on 14 Monday mornings yield x = 47 and s = 9 .4 mg/I. Obtain a 95% confidence interval for the mean amount of suspended solids. State any assumption you make about the population.
> A t distribution assigns more probability to large values than the standard normal. (a) Find t.05 for d.f = 12 and then evaluate P [ Z > t.05 ] . Verify that P [ T > t.05 ] is greater than P [Z > t.05] . (b) Examine the relation for d.f of 5 and 20, and
> Using software or the table of percentage points for the t distributions, find (a) t.05 when d.f = 7. (b) t.025 when d.f = 11. (c) The lower .05 point when d.f = 7. (d) The lower .05 point when d.f = 11.
> Refer to participants wore a counting device for a week, and each day they counted the number of times they thought about food. The average of the seven counts is intended to represent a typical day. For 19 males, we have times per day. (a) Make a graphi
> Refer to the computer anxiety scores (CARS) for males in the Data Bank. Conduct an a = .025 level of H0 : µ = 2.7 versus H1 : µ > 2.7.
> Refer to the data on the length (cm) of m ale grizzly bears given in the Data Bank. (a) Find a 99% confidence interval for the population mean. (b) Is the population mean length for all m ale grizzly b ears in Alaska contained in this interval? (c) Ex
> Refer to the computer output concerning the head length (cm) of male grizzly bears in Exercise 9.68. (a) Is the population mean head length for all m ale bears in the study area contained in this interval ? (b) Explain why you are 95% confident that it
> The probability distribution of a random variable X is given by the function (a) Calculate the numerical probabilities and list the distribution. (b) Calculate the mean and standard deviation of X.
> Refer to the data on the head length (cm) of male grizzly bears given in the Data Bank. A computer calculation for a test of H0 : µ = 21 versus H1 : µ ≠21 is given below. (a) What is the conclusion if you test
> Refer to the water quality data. Perform a test of hypotheses with the intent of showing that the population standard deviation is less than 18.0. Take a = .05.
> Refer to the data of Exercise 9.60. Is there strong evidence that the standard deviation for the efficiency of the new model is below 3.0? Data from Exercise 9.60: Combustion efficiency measurements were recorded for 10 home heating furnaces of a new mo
> Conduct a test of hypothesis with the intent of establishing that the mean bottle life is different from 55 .0 days. (a) Formulate the null and alternative hypotheses. (b) Determine the test statistic. (c) Give the form of the rejection region. (d) W
> Use software to find (a) The 90th percentile of x2 wh en d.f = 13. (b) The 10th percentile of x2 when d.f = 4. (c) The median of x2 when d.f = 32. (d) The 1st percentile of x2 when d.f. = 46.
> Use software to find (a) x2.05 with d.f = 3 . (b) x2.025 with d .f = 24. (c) The lower .05 point with d.f = 7. (d) The lower .025 point with d .f. = 32.
> Times to finish a sixteen ounce bottle of mayonnaise, were recorded by a sample of 11 purchasers. It is determined that Σxi = 645.7 days and Σ(xi - x)2 = 198.41. (a) Obtain a point estimate of the population mean life µ and its 90% error margin . (b) Ob
> A person with asthma took measurements by blowing into a peak-flow meter on seven consecutive days. / (a) Obtain a 95% confidence interval for the population mean peak-flow. (b) Conduct an a = .10 level test of H0 : µ = 453 versus H1 : µ ≠ 453.
> Combustion efficiency measurements were recorded for 10 home heating furnaces of a new model. The sample mean and standard deviation were found to be 73.2 and 2.74, respectively. Do these results provide strong evidence that the average efficiency of the
> A car advertisement asserts that with the new collapsible bumper system, the average body repair cost for the damages sustained in a collision impact of 10 miles per hour does not exceed $1500. To test the validity of this claim, 5 cars are crashed into
> Suppose the probability distribution of a random variable X has the distribution f( X) = 60/77 1/x for x = 2, 3, 4, 5 Calculate the mean and standard deviation of this distribution.
> The supplier of a particular brand of vitamin pills claims that the average potency of these pills after a certain exposure to heat and humidity is at least 65. Before buying these pills, a distributor wants to verify the supplier's claim is valid. To th
> Refer to concerning the yield of green gasoline. Conduct a test of hypothesis which is intended to show that the mean product volume is greater than 2. 7 5 liters. (a) Formulate the null and alternative hypotheses. (b) Determine the test statistic. (c
> Referring to Exercise 9 .55, test H0 : µ = 2.8 versus H1 : µ ≠2.8 using a = .02. Data from Exercise 9.55: In a study of head injuries to ice hockey players the number of hits were monitored electronically by
> In a study of head injuries to ice hockey players the number of hits were monitored electronically by equipping approved helmets with accelerometers that measured head acceleration (m/s2) when a player was hit. The researchers counted the number of serio
> Refer to the data on the heights of red pine seedlings in Exercise 8.3. Use MINITAB to: (a) Find a 97% percent confidence interval for the mean height. (b) Test H0 : µ = 1.9 versus H1 : µ ≠1.9 centimeters wi
> Refer to the data on percent malt extract in the Data Bank. A computer summary of a level a = .05 test of H0 : µ = 77 versus a two-sided alternative and a 95% confidence interval is given below: (a) Will the 98% confidence interval for mean
> Refer to the data on the computer attitude score (CAS) in the Data Bank. A computer summary of a level a = .05 test of H0 : µ = 2.6 versus a two-sided alternative and a 95% confidence interval is given below. (a) Will the 99% confidence inte
> Consider the problem of testing H0: µ = 10 versus H1 :µ > 10 with n = 64, u = 2 (known), and a = .025 . The rejection region of this test is given by Suppose we wish to calculate the power of this test at the alternative &Aci
> Refer to Exercise 8.2 where participants wore a counting device for a week, and each day they counted the number of times they thought about food. The average of the seven daily counts, for each of n = 65 participants, are summarized by the statistics n
> A genetic model suggests that 80% of the plants grown from a cross between two given strains of seeds will be of the dwarf variety. After breeding 200 of these plants, 136 were observed to be of the dwarf variety. (a) Does this observation strongly cont
> Upon examination of the claims records of 280 policy holders over a period of five years, an insurance company makes an empirical determination of the probability distribution of X = number of claims in five years. (a) Calculate the expected value of X.
> Each year, an insurance company reviews its claim experience in order to set future rates. Regarding their damage-only automobile insurance policies, at least one claim was made on 2073 of the 12,299 policies in effect for the year. Treat these data as a
> In one 45-day period, American Airlines flew 152 flights from Chicago, Illinois, to Austin, Texas. Of these, 22 arrived late. Treat this as a random sample and conduct a test with the intent of establishing that the population proportion of late flights
> With reference to Exercise 8.90, conduct a test with the intent of establishing that p > .20. (a) Formulate the null and alternative hypotheses. (b) Determine the test statistic. (c) Give the form of the rejection region. (d) What is the conclusion t
> Out of a sample of n = 625 students interviewed, 139 had missed at least one class last week. Obtain a 95% confidence interval for p = proportion of all students that missed at least one class last week.
> With reference to Exercise 8.88, (a) Conduct a test of size .OS with the intent of establishing that the proportion today is larger than .67. (b) Find a 95% confidence interval for that proportion. Data from Exercise 8.88: In a recent year, 67% of per
> In a recent year, 67% of persons 22-33 years old held passports. From a random sample of size n = 79 collected today, 61 are passport holders. (a) Estimate the proportion of persons 22-33 years old who hold passports today. (b) Estimate a 95% error mar
> The daily number of kayaks sold, X, at a water sports store has the probability distribution (a) Find the expected number of kayaks sold in a day. (b) Find the standard deviation of the number of kayaks sold in a day. (c) Suppose data from the next 64
> Refer to the data on the number of extracurricular activities in which 30 students participated in the past week. These data have n = 30, x = 1.925, s = 1.607 activities (a) Obtain a 98% confidence interval for µ, the population mean number of activiti
> A zoologist wishes to estimate the mean blood sugar level of a species of animal when injected with a specified dosage of adrenaline. A sample of 55 animals of a common breed are injected with adrenaline, and their blood sugar measurements are recorded i
> Refer to Exercise 5.33, but suppose that the projects are scheduled consecutively with A in the first year and B in the second year. Th e company's chance of winning project A is still . 50. Instead of the assumption of independence, now assume that if t
> A food service manager wants to be 95% certain that the error in the estimate of the mean number of sandwiches dispensed over the lunch hour is l O or less. What sample size should be selected if a preliminary sample suggests (a) ( = 40? (b) ( = 80?
> By what factor should the sample size be increased to reduce the standard error of X to (a) One-half its original value? (b) One-fourth its original value?
> The time it takes for a taxi to drive from the office to the airport was recorded on 40 occasions. It was found that x = 47 minutes and s = 5 minutes. Give (a) An estimate of µ = population mean time to drive. (b) An approximate 95.4% error margin.
> A student in a large lecture section asked students how much they paid for a used copy of the text. The n = 38 responses yielded (a) Give a point estimate of µ, the mean price paid. (b) Determine the estimated standard error. (c) Calculate
> Refer to where the number of automobile accidents reported per month were recorded for an intersection. The sample size is n = 59, x = 1.949, and s = 1.558 accidents. (a) Give a point estimate ofµ, the mean number of accidents reported per month. (b)
> Refer to the grizzly bear data given in the Data Bank. Use MINITAB or some other package program to: (a) Find a 95% large sample confidence interval for the mean weight in pounds of all bears living in that area. (b) Construct a histogram to determine i
> Refer to the physical fitness data given in the Data Bank. Use MINITAB or some other package program to: (a) Find a 97% large sample confidence interval for the pretest number of sit-ups. (b) Construct a histogram to determine if the underlying distribu
> Refer to the male salmon data given in of the Data Bank. Use MINITAB or some other package program to find a 90% large sample confidence interval for the mean freshwater growth.
> Referring to speedy lizard data, obtain a 95% confidence interval for the mean speed of that genus.
> Instead of performing a fixed number of Bernoulli trials, an experimenter performs trials until the first success occurs. The number of successes is now fixed at 1, but the number of trials Y is now random. It can assume any of the values 1, 2, 3, and so
> A construction company submits bids for two projects. Listed here are the profit and the probability of winning each project. Assume that the outcomes of the two bids are independent. (a) List the possible outcomes (win/not win) for the two projects and
> An inspector samples bags of potato chips to see if they fall short of the weight, 14 ounces, printed on the bag. Samples of 20 bags are selected and the number with weight less than 14 ounces is recorded. (a) Make a p chart using the centerline and con
> Among the library's books purchased in the past three years, 1.2 % cannot be located. A random sample of 150 books is selected from a much larger number purchased in the last three years. Approximate the probability of (a) Exactly 2 cannot be located.
> A Poisson distribution describes X = the number of bad checks a mega-store receives each day. If this store receives an average of 2 bad checks per day, (a) Find the mean and variance. What are the probabilities it will receive. (b) 3 bad checks in a gi
> Jones claims to have extrasensory perception (ESP). In order to test the claim, a psychologist shows Jones five cards that carry different pictures. Then Jones is blindfolded and the psychologist selects one card and asks Jones to identify the picture. T
> Only 30% of the people in a large city feel that its mass transit system is adequate. If 20 persons are selected at random, find the probability that 10 or more will feel that the system is adequate. Find the probability that exactly 10 will feel that th
> For a binomial distribution with p = .15, find the smallest number n such that 1 success is more probable than no successes in n trials.
> Refer to the population of social science majors in Exercise 5.115 but change the sample size to n = 5. Using the binomial table, (a) List the probability distribution. (b) Plot the probability histogram. (c) Calculate E ( X) and Var ( X) from the ent
> At one large midwest university, about 40% of the college seniors have a social science major. Fourteen seniors are selected at random. Let X denote the number that have a social science major. Determine (a) p [ 3 ≤ X ≤ g ] (b) p [ 3 < X ≤ g ] (c) P[3 <
> A school newspaper claims that 70% of the students support its view on a campus issue. A random sample of 20 students is taken, and 10 students agree with the newspaper. Find P[10 or less agree] if 70% support the view and comment on the plausibility of
> For each situation, state if a binomial distribution is reasonable for the random variable X. Justify your answer. (a) A multiple-choice examination consists of 10 problems, each of which has 5 suggested answers. A student marks answers by pure guesses
> In bidding for a contract to cater a large wedding, a caterer expects she will have a net profit of $3000 if she wins the contract and net loss of $60 if h er bid fails. If the probability of getting the contract is .3, calculate her expected return.
> National safety statistics suggest that about 33% of the persons treated in an emergency room because of moped accidents are under 16 years of age. Suppose you count the number of persons under 16 among the next 14 moped accident victims to come to the e
> The probability that a voter will believe a rumor about a politician is .3. If 20 voters are told individually: (a) Find the probability that none of the 20 believes the rumor. (b) Find the probability that seven or more believe the rumor. (c) Det erm
> A viral infection is spread by contact with an infected person. Let the probability that a healthy person gets the infection in one contact be p = .4. (a) An infected person has contact with six healthy persons. Specify the distribution of X = No. of pe
> The proportion of people having the blood type O-positive in a large southern city is .38. For two randomly selected donors: (a) Find the probability of at least one type 0 . (b) Find the expected number of type 0 . (c) Repeat parts (a) and (b) if the
> If in three Bernoulli trials the probability that the first two trials are both failures is 9/49 what is the probability that the first two are successes and the third is a failure?
> A basketball team scores 35% of the times it gets the ball. Find the probability that the first basket occurs on its third possession.
> If the probability of having a male child is . 5, find the probability that the third child is the first son.
> Give an example of repeated trials with two possible outcomes where: (a) The model of Bernoulli trials is reasonable. (b) The condition of independence is violated. (c) The condition of equal P ( S) is violated.
> Is the model of Bernoulli trials plausible in each of the following situations? Identify any serious violations of the conditions. (a) A beginning golfer tries 40 putts, 5 feet from the hole, while practicing on the putting green. (b) Persons applying f
> Let the random variable Y denote the proportion of times a head occurs in three tosses of a coin, that is, Y = ( No. of heads in 3 tosses )/ 3. (a) Obtain the probability distribution Y. (b) Draw the probability histogram. (c) Calculate the E ( Y) and
> A book club announces a sweepstakes in order to attract new subscribers. The prizes and the corresponding chances are listed here (typically, the prizes are listed in bold print in an advertisement flyer while the chances are entered in fine print or not
> A probability distribution can also be described by a function that gives the accumulated probability at or below each value of X. Specifically, Cumulative distribution function at c = Sum of probabilities of all values x ≤ c For the
> Suppose that X can take the values 0, 1, 2, 3, and 4, and the probability distribution of X is incompletely specified by the function Find(a) f(4) (b)P [X ≥ 2] (c) E(X)and (d) sd(X).
> A roulette wheel has 38 slots, of which 18 are red, 18 black, and 2 green. A gambler will play three times, each time betting $5 on red . The gambler gets $ 10 if red occurs and loses the bet otherwise. Let X denote the net gain of the gambler in 3 plays
> John and two of his friends have one-on-one basketball tournaments almost every week. Each person plays each other person once. Let X be the number of games that John wins next week X . Based on the results of the games over the past year, John construct
> A botany student is asked to match the popular names of three house plants with their obscure botanical names. Suppose the student never heard of these names and is trying to match by sheer guess. Let X denote the number of correct matches. (a) Obtain t
> Suppose the number of parking tickets X issued during a police officer's shift has the probability distribution (a) Find the mean and standard deviation of the number of parking tickets issued. (b) Let Find (c) Suppose the numbers of tickets issued on di
> The number of overnight emergency calls X to the answering service of a heating and air conditioning firm have the probabilities .05, .1, .15, .35, .20, and .15 for 0, 1, 2, 3, 4, and 5 calls, respectively. (a) Find the probability of fewer than 3 calls
> In the finals of a match play golf tournament, the winner will get $90,000 and the loser$ 15,000. Find the expected winnings of player B if (a) the two finalists are evenly matched and (b) player B has probability .8 of winning.
> A student buys a lottery ticket for $2. The prize is a bicycle worth $500. The winning ticket will be chosen at random from 2000 tickets that were sold. (a) What is the probability that the student will win a bicycle? (b) Determine the student's expect
> Refer to Exercise 5.91. (a) List the x values that lie in the interval µ - (, to µ + (, and calculate P [ µ - (≤ X ≤ µ + ( ] . (b) List the x values that lie in
> Referring to Exercise 5.25, find the mean and standard deviation of the number of customers. Data from Exercise 5.25: Based on recent records, the manager of a car painting center has determined the following probability distribution for the number of c
> Two of the integers { 1, 3, 5, 6, 7 } are chosen at random without replacement. Let X denote the difference = largest -smallest. (a) List all choices and the corresponding values of X. (b) List the distinct values of X and det ermine their probabilities
> The following distribution has been proposed for the number of times a student will eat at a gourmet restaurant dinner next week. (a) Calculate the mean and variance. (b) Plot the probability histogram and locate µ.
> Refer to the monthly intersection accident data. Considering an even longer record leads to a distribution for X = number of accidents in a month. (a) Calculate E(X). (b) Calculate sd ( X). (c) Draw the probability histogram and locate the mean.
> A list of the world's 10 largest companies, in terms of revenue, contains 4 from the United States, 3 from China, and 1 each from Germany, Japan, and the Netherlands. A potential investor randomly selects 3 of the companies to research further. (a) Find

