Question: An important piece of landing equipment must
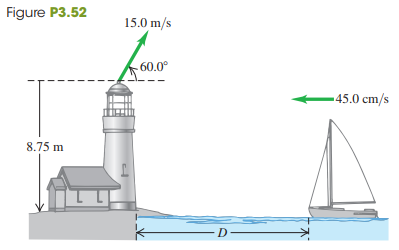
An important piece of landing equipment must be thrown to a ship, which is moving at 45.0 cm>s, before the ship can dock. This equipment is thrown at 15.0 m>s at 60.0° above the horizontal from the top of a tower at the edge of the water, 8.75 m above the ship’s deck (Fig. P3.52). For this equipment to land at the front of the ship, at what distance D from the dock should the ship be when the equipment is thrown? Ignore air resistance.
Fig. P3.52:
Transcribed Image Text:
Figure P3.52 15.0 m/s 60.0° •45.0 cm/s 8.75 m -D-
> If C ⃗ = A ⃗ + B ⃗, what must be true about the directions and magnitudes of A ⃗ and B ⃗ if C = A + B? What must be true about the directions and magnitudes of A ⃗ and B ⃗ if C = 0?
> Under constant acceleration the average velocity of a particle is half the sum of its initial and final velocities. Is this still true if the acceleration is not constant? Explain.
> Can you find a vector quantity that has a magnitude of zero but components that are not zero? Explain. Can the magnitude of a vector be less than the magnitude of any of its components? Explain.
> Air traffic controllers give instructions called “vectors” to tell airline pilots in which direction they are to fly. If these are the only instructions given, is the name “vector” used correctly? Why or why not?
> The “direction of time” is said to proceed from past to future. Does this mean that time is a vector quantity? Explain.
> An automobile is traveling west. Can it have a velocity toward the west and at the same time have an acceleration toward the east? Under what circumstances?
> A package falls out of an airplane that is flying in a straight line at a constant altitude and speed. If you ignore air resistance, what would be the path of the package as observed by the pilot? As observed by a person on the ground?
> A circular racetrack has a radius of 500 m. What is the displacement of a bicyclist when she travels around the track from the north side to the south side? When she makes one complete circle around the track? Explain.
> Is the vector (
> Three archers each fire four arrows at a target. Joe’s four arrows hit at points 10 cm above, 10 cm below, 10 cm to the left, and 10 cm to the right of the center of the target. All four of Moe’s arrows hit within 1 cm of a point 20 cm from the center, a
> What are the units of volume? Suppose another student tells you that a cylinder of radius r and height h has volume given by pr3h. Explain why this cannot be right.
> The quantity p = 3.14159c is a number with no dimensions, since it is a ratio of two lengths. Describe two or three other geometrical or physical quantities that are dimensionless.
> Describe how you could measure the thickness of a sheet of paper with an ordinary ruler.
> What physical phenomena (other than a pendulum or cesium clock) could you use to define a time standard?
> Under what conditions is average velocity equal to instantaneous velocity?
> A projectile moves in a parabolic path without air resistance. Is there any point at which
> Suppose you are asked to compute the tangent of 5.00 meters. Is this possible? Why or why not?
> A book slides off a horizontal tabletop. As it leaves the table’s edge, the book has a horizontal velocity of magnitude v0. The book strikes the floor in time t. If the initial velocity of the book is doubled to 2v0, what happens to (a) the time the book
> What is your height in centimeters? What is your weight in newtons?
> Does the speedometer of a car measure speed or velocity? Explain.
> Each of the values of h and R has some measurement error: The muzzle speed is not precisely the same each time, and the barrel isn’t precisely horizontal. So you use all of the measurements to get the best estimate of v0. No wind is blowing, so you decid
> You have constructed a hair-spray-powered potato gun and want to find the muzzle speed v0 of the potatoes, the speed they have as they leave the end of the gun barrel. You use the same amount of hair spray each time you fire the gun, and you have confirm
> A spring-gun projects a small rock from the ground with speed v0 at an angle u0 above the ground. You have been asked to determine v0. From the way the spring-gun is constructed, you know that to a good approximation v0 is independent of the launch angle
> Two soccer players, Mia and Alice, are running as Alice passes the ball to Mia. Mia is running due north with a speed of 6.00 m>s. The velocity of the ball relative to Mia is 5.00 m/s in a direction 30.0o east of south. What are the magnitude and directi
> An elevator is moving upward at a constant speed of 2.50 m/s. A bolt in the elevator ceiling 3.00 m above the elevator floor works loose and falls. (a) How long does it take for the bolt to fall to the elevator floor? What is the speed of the bolt just a
> In a World Cup soccer match, Juan is running due north toward the goal with a speed of 8.00 m/s relative to the ground. A teammate passes the ball to him. The ball has a speed of 12.0 m/s and is moving in a direction 37.0° east of north, relative to the
> When a train’s velocity is 12.0 m/s eastward, raindrops that are falling vertically with respect to the earth make traces that are inclined 30.0° to the vertical on the windows of the train. (a) What is the horizontal component of a drop’s velocity with
> An airplane pilot sets a compass course due west and maintains an airspeed of 220 km/h. After flying for 0.500 h, she finds herself over a town 120 km west and 20 km south of her starting point. (a) Find the wind velocity (magnitude and direction). (b) I
> A student sits atop a platform a distance h above the ground. He throws a large firecracker horizontally with a speed v. However, a wind blowing parallel to the ground gives the firecracker a constant horizontal acceleration with magnitude a. As a result
> Redraw Fig. 3.11a if
> In the middle of the night you are standing a horizontal distance of 14.0 m from the high fence that surrounds the estate of your rich uncle. The top of the fence is 5.00 m above the ground. You have taped an important message to a rock that you want to
> A firefighting crew uses a water cannon that shoots water at 25.0 m/s at a fixed angle of 53.0° above the horizontal. The firefighters want to direct the water at a blaze that is 10.0 m above ground level. How far from the building should they position t
> A cart carrying a vertical missile launcher moves horizontally at a constant velocity of 30.0 m/s to the right. It launches a rocket vertically upward. The missile has an initial vertical velocity of 40.0 m/s relative to the cart. (a) How high does the r
> Henrietta is jogging on the sidewalk at 3.05 m/s on the way to her physics class. Bruce realizes that she forgot her bag of bagels, so he runs to the window, which is 38.0 m above the street level and directly above the sidewalk, to throw the bag to her.
> A 76.0-kg rock is rolling horizontally at the top of a vertical cliff that is 20 m above the surface of a lake (Fig. P3.65). The top of the vertical face of a dam is located 100 m from the foot of the cliff, with the top of the dam level with the surface
> A 2.7-kg ball is thrown upward with an initial speed of 20.0 m>s from the edge of a 45.0-m-high cliff. At the instant the ball is thrown, a woman starts running away from the base of the cliff with a constant speed of 6.00 m/s. The woman runs in a straig
> A 2.7-kg ball is thrown upward with an initial speed of 20.0 m>s from the edge of a 45.0-m-high cliff. At the instant the ball is thrown, a woman starts running away from the base of the cliff with a constant speed of 6.00 m/s. The woman runs in a straig
> A physics professor did daredevil stunts in his spare time. His last stunt was an attempt to jump across a river on a motorcycle (Fig. P3.63). The takeoff ramp was inclined at 53.0°, the river was 40.0 m wide, and the far bank was 15.0 m lower
> A rock is thrown with a velocity v0, at an angle of a0 from the horizontal, from the roof of a building of height h. Ignore air resistance. Calculate the speed of the rock just before it strikes the ground, and show that this speed is independent of a0.
> Suppose that the boy in Problem 3.60 throws the ball upward at 60.0° above the horizontal, but all else is the same. Repeat parts (a) and (b) of that problem. Data from Problem 3.60: A boy 12.0 m above the ground in a tree throws a ball for his dog, wh
> A stone is thrown into the air at an angle above the horizontal and feels negligible air resistance. Which graph in Fig. Q3.16 best depicts the stone’s speed v as a function of time t while it is in the air? Fig. Q3.16: (a) (b) (c
> A boy 12.0 m above the ground in a tree throws a ball for his dog, who is standing right below the tree and starts running the instant the ball is thrown. If the boy throws the ball horizontally at 8.50 m/s, (a) how fast must the dog run to catch the bal
> A snowball rolls off a barn roof that slopes downward at an angle of 40° (Fig. P3.59). The edge of the roof is 14.0 m above the ground, and the snowball has a speed of 7.00 m>s as it rolls off the roof. Ignore air resistance. (a) How far fr
> In Canadian football, after a touchdown the team has the opportunity to earn one more point by kicking the ball over the bar between the goal posts. The bar is 10.0 ft above the ground, and the ball is kicked from ground level, 36.0 ft horizontally from
> A grasshopper leaps into the air from the edge of a vertical cliff, as shown in Fig. P3.57. Find (a) the initial speed of the grasshopper and (b) the height of the cliff. Fig. P3.57: Figure P3.57 6.74 cm 50.0° Not to scale 1.06 m
> A water hose is used to fill a large cylindrical storage tank of diameter D and height 2D. The hose shoots the water at 45° above the horizontal from the same level as the base of the tank and is a distance 6D away (Fig. P3.56). For what range
> A baseball thrown at an angle of 60.0° above the horizontal strikes a building 18.0 m away at a point 8.00 m above the point from which it is thrown. Ignore air resistance. (a) Find the magnitude of the ball’s initial velocity (the velocity with which th
> An airplane is dropping bales of hay to cattle stranded in a blizzard on the Great Plains. The pilot releases the bales at 150 m above the level ground when the plane is flying at 75 m/s in a direction 55° above the horizontal. How far in front of the ca
> According to Guinness World Records, the longest home run ever measured was hit by Roy “Dizzy” Carlyle in a minor league game. The ball traveled 188 m (618 ft) before landing on the ground outside the ballpark. (a) If the ball’s initial velocity was in a
> A toy rocket is launched with an initial velocity of 12.0 m>s in the horizontal direction from the roof of a 30.0-m-tall building. The rocket’s engine produces a horizontal acceleration of (1.60 m/s3)t, in the same direction as the initial velocity, but
> You are on the west bank of a river that is flowing north with a speed of 1.2 m/s. Your swimming speed relative to the water is 1.5 m/s, and the river is 60 m wide. What is your path relative to the earth that allows you to cross the river in the shortes
> A cannon, located 60.0 m from the base of a vertical 25.0-m-tall cliff, shoots a 15-kg shell at 43.0° above the horizontal toward the cliff. (a) What must the minimum muzzle velocity be for the shell to clear the top of the cliff? (b) The ground at the t
> An airplane is flying with a velocity of 90.0 m/s at an angle of 23.0° above the horizontal. When the plane is 114 m directly above a dog that is standing on level ground, a suitcase drops out of the luggage compartment. How far from the dog will the sui
> A model car starts from rest and travels in a straight line. A smartphone mounted on the car has an app that transmits the magnitude of the car’s acceleration (measured by an accelerometer) every second. The results are given in the tab
> In a physics lab experiment, you release a small steel ball at various heights above the ground and measure the ball’s speed just before it strikes the ground. You plot your data on a graph that has the release height (in meters) on the vertical axis and
> In your physics lab you release a small glider from rest at various points on a long, frictionless air track that is inclined at an angle u above the horizontal. With an electronic photocell, you measure the time t it takes the glider to slide a distance
> Cars A and B travel in a straight line. The distance of A from the starting point is given as a function of time by xA(t)= at + bt2, with a = 2.60 m/s and b = 1.20 m/s2. The distance of B from the starting point is xB(t)= gt2 - dt3, with g = 2.80 m/s2 an
> A ball is thrown straight up from the ground with speed v0. At the same instant, a second ball is dropped from rest from a height H, directly above the point where the first ball was thrown upward. There is no air resistance. (a) Find the time at which t
> An object is moving along the x-axis. At t = 0 it has velocity v0x = 20.0 m/s. Starting at time t = 0 it has acceleration ax = -Ct, where C has units of m/s3. (a) What is the value of C if the object stops in 8.00 s after t = 0? (b) For the value of C ca
> You are climbing in the High Sierra when you suddenly find yourself at the edge of a fog-shrouded cliff. To find the height of this cliff, you drop a rock from the top; 8.00 s later you hear the sound of the rock hitting the ground at the foot of the cli
> A helicopter carrying Dr. Evil takes off with a constant upward acceleration of 5.0 m/s2. Secret agent Austin Powers jumps on just as the helicopter lifts off the ground. After the two men struggle for 10.0 s, Powers shuts off the engine and steps out of
> Raindrops hitting the side windows of a car in motion often leave diagonal streaks even if there is no wind. Why? Is the explanation the same or different for diagonal streaks on the windshield?
> A physics teacher performing an outdoor demonstration suddenly falls from rest off a high cliff and simultaneously shouts “Help.” When she has fallen for 3.0 s, she hears the echo of her shout from the valley floor below. The speed of sound is 340 m/s. (
> During your summer internship for an aerospace company, you are asked to design a small research rocket. The rocket is to be launched from rest from the earth’s surface and is to reach a maximum height of 960 m above the earth’s surface. The rocket’s eng
> In the first stage of a two-stage rocket, the rocket is fired from the launch pad starting from rest but with a constant acceleration of 3.50 m/s2 upward. At 25.0 s after launch, the second stage fires for 10.0 s, which boosts the rocket’s velocity to 13
> Two stones are thrown vertically upward from the ground, one with three times the initial speed of the other. (a) If the faster stone takes 10 s to return to the ground, how long will it take the slower stone to return? (b) If the slower stone reaches a
> A flowerpot falls off a windowsill and passes the window of the story below. Ignore air resistance. It takes the pot 0.380 s to pass from the top to the bottom of this window, which is 1.90 m high. How far is the top of the window below the windowsill fr
> Sam heaves a 16-lb shot straight up, giving it a constant upward acceleration from rest of 35.0 m/s2 for 64.0 cm. He releases it 2.20 m above the ground. Ignore air resistance. (a) What is the speed of the shot when Sam releases it? (b) How high above th
> An entertainer juggles balls while doing other activities. In one act, she throws a ball vertically upward, and while it is in the air, she runs to and from a table 5.50 m away at an average speed of 3.00 m/s, returning just in time to catch the falling
> A certain volcano on earth can eject rocks vertically to a maximum height H. (a) How high (in terms of H) would these rocks go if a volcano on Mars ejected them with the same initial velocity? The acceleration due to gravity on Mars is 3.71 m/s2; ignore
> You are on the roof of the physics building, 46.0 m above the ground (Fig. P2.70). Your physics professor, who is 1.80 m tall, is walking alongside the building at a constant speed of 1.20 m/s. If you wish to drop an egg on your professorâ€
> The acceleration of a particle is given by ax(t) = -2.00 m/s2 +(3.00 m/s3)t. (a) Find the initial velocity v0x such that the particle will have the same x-coordinate at t = 4.00 s as it had at t = 0. (b) What will be the velocity at t = 4.00 s ?
> In uniform circular motion, what are the average velocity and average acceleration for one revolution? Explain.
> An object’s velocity is measured to be vx(t) = a - bt2, where a = 4.00 m/s and b = 2.00 m/s3. At t = 0 the object is at x = 0. (a) Calculate the object’s position and acceleration as functions of time. (b) What is the object’s maximum positive displaceme
> The driver of a car wishes to pass a truck that is traveling at a constant speed of 20.0 m/s (about 45 mi/h). Initially, the car is also traveling at 20.0 m/s, and its front bumper is 24.0 m behind the truck’s rear bumper. The car accelerates at a consta
> You are standing at rest at a bus stop. A bus moving at a constant speed of 5.00 m/s passes you. When the rear of the bus is 12.0 m past you, you realize that it is your bus, so you start to run toward it with a constant acceleration of 0.960 m/s2. How f
> A car and a truck start from rest at the same instant, with the car initially at some distance behind the truck. The truck has a constant acceleration of 2.10 m/s2, and the car has an acceleration of 3.40 m/s2. The car overtakes the truck after the truck
> Two cars start 200 m apart and drive toward each other at a steady 10 m/s. On the front of one of them, an energetic grasshopper jumps back and forth between the cars (he has strong legs!) with a constant horizontal velocity of 15 m/s relative to the gro
> A ball starts from rest and rolls down a hill with uniform acceleration, traveling 200 m during the second 5.0 s of its motion. How far did it roll during the first 5.0 s of motion?
> The engineer of a passenger train traveling at 25.0 m/s sights a freight train whose caboose is 200 m ahead on the same track (Fig. P2.62). The freight train is traveling at 15.0 m/s in the same direction as the passenger train. The engineer of the passe
> A gazelle is running in a straight line (the x-axis). The graph in Fig. P2.61 shows this animal’s velocity as a function of time. During the first 12.0 s, find (a) the total distance moved and (b) the displacement of the gazelle. (c) Sk
> A subway train starts from rest at a station and accelerates at a rate of 1.60 m/s2 for 14.0 s. It runs at constant speed for 70.0 s and slows down at a rate of 3.50 m/s2 until it stops at the next station. Find the total distance covered.
> A rocket carrying a satellite is accelerating straight up from the earth’s surface. At 1.15 s after liftoff, the rocket clears the top of its launch platform, 63 m above the ground. After an additional 4.75 s, it is 1.00 km above the ground. Calculate th
> When you drop an object from a certain height, it takes time T to reach the ground with no air resistance. If you dropped it from three times that height, how long (in terms of T) would it take to reach the ground?
> A brick is dropped from the roof of a tall building. After it has been falling for a few seconds, it falls 40.0 m in a 1.00-s time interval. What distance will it fall during the next 1.00 s? Ignore air resistance.
> Earthquakes produce several types of shock waves. The most well-known are the P-waves (P for primary or pressure) and the S-waves (S for secondary or shear). In the earth’s crust, P-waves travel at about 6.5 km/s and S-waves move at about 3.5 km/s. The t
> A lunar lander is descending toward the moon’s surface. Until the lander reaches the surface, its height above the surface of the moon is given by y(t)= b - ct + dt2, where b = 800 m is the initial height of the lander above the surface, c = 60.0 m/s, an
> A typical male sprinter can maintain his maximum acceleration for 2.0 s, and his maximum speed is 10 m/ s. After he reaches this maximum speed, his acceleration becomes zero, and then he runs at constant speed. Assume that his acceleration is constant du
> The Mars Polar Lander spacecraft was launched on January 3, 1999. On December 3, 1999, the day Mars Polar Lander impacted the Martian surface at high velocity and probably disintegrated, the positions of the earth and Mars were given by these coordinates
> You are a mechanical engineer working for a manufacturing company. Two forces, F S 1 and F S 2, act on a component part of a piece of equipment. Your boss asked you to find the magnitude of the larger of these two forces. You can vary the angle between F
> You are a team leader at a pharmaceutical company. Several technicians are preparing samples, and you want to compare the densities of the samples (density = mass>volume) by using the mass and volume values they have reported. Unfortunately, you did n
> Later in our study of physics we will encounter quantities represented by (
> You are given vectors
> Two vectors
> Prove these statements: (a) As long as you can ignore the effects of the air, if you throw anything vertically upward, it will have the same speed when it returns to the release point as when it was released. (b) The time of flight will be twice the time
> The scalar product of vectors
> Obtain a unit vector perpendicular to the two vectors given in Exercise 1.41. Exercise 1.41: Given two vectors
> Vector
> A cube is placed so that one corner is at the origin and three edges are along the x-, y-, and z-axes of a coordinate system (Fig. P1.80). Use vectors to compute (a) the angle between the edge along the z-axis (line ab) and the diagonal from the origin t
> Vectors

