Question: As we mentioned on page 378, the
As we mentioned on page 378, the following relationship holds between hypothesis tests and confidence intervals for one-mean z-procedures: For a two-tailed hypothesis test at the significance level α, the null hypothesis H0: μ = μ0 will be rejected in favor of the alternative hypothesis Ha: μ ≠ μ0 if and only if μ0 lies outside the (1 − α)-level confidence interval for μ. In each case, illustrate the preceding relationship by obtaining the appropriate one-mean z-interval and comparing the result to the conclusion of the hypothesis test in the specified exercise.
a. Exercise 9.84
b. Exercise 9.87
Data from Exercise 9.84:
The average lactation (nursing) period of all earless seals is 23 days. Grey seals are one of several types of earless seals. The length of time that a female grey seal nurses her pup is studied by S. Twiss et al. in the article “Variation in Female Grey Seal (Halichoerus grypus) Reproductive Performance Correlates to Proactive-Reactive Behavioural Types” (PLOS ONE 7(11): e49598. doi:10.1371/journal.pone.0049598). A sample of 14 female grey seals had the following lactation periods, in days.
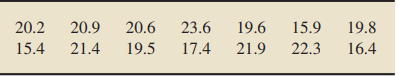
At the 5% significance level, do the data provide sufficient evidence to conclude that the mean lactation period of grey seals differs from 23 days? Assume that the population standard deviation is 3.0 days.
Data from Exercise 9.87:
According to the Bureau of Crime Statistics and Research of Australia, as reported on Lawlink, the mean length of imprisonment for motor-vehicle-theft offenders in Australia is 16.7 months. One hundred randomly selected motor-vehicle-theft offenders in Sydney, Australia, had a mean length of imprisonment of 17.8 months. At the 5% significance level, do the data provide sufficient evidence to conclude that the mean length of imprisonment for motor-vehicle-theft offenders in Sydney differs from the national mean in Australia? Assume that the population standard deviation of the lengths of imprisonment for motor-vehicle-theft offenders in Sydney is 6.0 months.
> The cheetah (Acinonyx jubatus) is the fastest land mammal and is highly specialized to run down prey. The cheetah often exceeds speeds of 60 mph and, according to the online document “Cheetah Conservation in Southern Africa” (Trade & Environment Database
> In the online paper “A Comparison of Two Computer Fonts: Serif versus Ornate Sans Serif” (Usability News, Issue 5.3), researchers S. Morrison and J. Noyes studied whether the type of font used in a document affects reading speed or comprehension. The fon
> Refer to Exercise 10.128 and find a 98% confidence interval for the difference between the mean times to fatigue on a treadmill in a hot and humid environment after cooling down with cold water and after cooling down with an ice slurry. Data from Exerci
> Refer to Exercise 10.127 and obtain an 80% confidence interval for the difference between the mean corneal thickness of normal eyes and that of eyes with glaucoma. Data from Exercise 10.127: Glaucoma is a leading cause of blindness in the United States.
> Refer to Exercise 10.126 and find a 95% confidence interval for the mean difference in measurement by the weight and groove methods. Data from Exercise 10.126: R. Stichler et al. compared two methods of measuring treadwear in their paper “Measurement of
> Refer to Exercise 10.125 and find a 90% confidence interval for the weight gain that would be obtained, on average, by using the family therapy treatment. Data from Exercise 10.125: Anorexia nervosa is a serious eating disorder, particularly among young
> Refer to Exercise 10.124. a. Determine a 90% confidence interval for the additional sleep that would be obtained, on average, by using laevohysocyamine hydrobromide. b. Repeat part (a) for a 98% confidence level. Data from Exercise 10.124: In 1908, W. S
> we have presented a confidence interval (CI) for the difference, μ1 − μ2, between two population means. Interpret each confidence interval. 95% CI is from 15 to 20.
> Refer to Exercise 10.123. a. Determine a 95% confidence interval for the difference between the mean heights of cross-fertilized and self-fertilized Zea mays. b. Repeat part (a) for a 99% confidence level. Data from Exercise 10.123: Charles Darwin, auth
> Cooling down with a cold drink before exercise in the heat is believed to help an athlete perform. Researcher J. Dugas explored the difference between cooling down with an ice slurry (slushy) and with cold water in the article “Ice Slurry Ingestion Incre
> Glaucoma is a leading cause of blindness in the United States. N. Ehlers measured the corneal thickness of eight patients who had glaucoma in one eye but not in the other. The results of the study were published as the paper “On Corneal Thickness and Int
> The Information Please Almanac provides the number of children of each of the U.S. presidents. A frequency histogram for number of children by president, through President Barack H. Obama, is as follows. Is distribution (roughly) symmetric, right skewed,
> R. Stichler et al. compared two methods of measuring treadwear in their paper “Measurement of Treadwear of Commercial Tires” (Rubber Age, Vol. 73:2). Eleven tires were each measured for treadwear by two methods, one based on weight and the other on groov
> Anorexia nervosa is a serious eating disorder, particularly among young women. The following data provide the weights, in pounds, of 17 anorexic young women before and after receiving a family therapy treatment for anorexia nervosa. Does family therapy a
> In 1908, W. S. Gosset published “The Probable Error of a Mean” (Biometrika, Vol. 6, pp. 1–25). In this pioneering paper, published under the pseudonym “Student,” he introduced what later became known as Student’s t-distribution. Gosset used the following
> Charles Darwin, author of Origin of Species, investigated the effect of cross-fertilization on the heights of plants. In one study he planted 15 pairs of Zea mays plants. Each pair consisted of one cross-fertilized plant and one self-fertilized plant gro
> The null hypothesis is H0: μ1 = μ2 and the alternative hypothesis is as specified. We have provided data from a simple random paired sample from the two populations under consideration. In each case, use the paired t-test to perform the required hypothes
> The null hypothesis is H0: μ1 = μ2 and the alternative hypothesis is as specified. We have provided data from a simple random paired sample from the two populations under consideration. In each case, use the paired t-test to perform the required hypothes
> The null hypothesis is H0:μ1 = μ2 and the alternative hypothesis is as specified. We have provided data from a simple random paired sample from the two populations under consideration. In each case, use the paired t-test to perform the required hypothesi
> Identify the assumption for using the two-means z-test and the two-means z-interval procedure that renders those procedures generally impractical.
> The null hypothesis is H0:μ1 = μ2 and the alternative hypothesis is as specified. We have provided data from a simple random paired sample from the two populations under consideration. In each case, use the paired t-test to perform the required hypothesi
> The null hypothesis is H0:μ1 = μ2 and the alternative hypothesis is as specified. We have provided data from a simple random paired sample from the two populations under consideration. In each case, use the paired t-test to perform the required hypothesi
> We have drawn a smooth curve that represents a distribution. In each case, do the following: a. Identify the shape of the distribution with regard to modality. b. Identify the shape of the distribution with regard to symmetry (or non-symmetry). c. If the
> The null hypothesis is H0:μ1 = μ2 and the alternative hypothesis is as specified. We have provided data from a simple random paired sample from the two populations under consideration. In each case, use the paired t-test to perform the required hypothesi
> In the article “Comparison of Fiber Counting by TV Screen and Eyepieces of Phase Contrast Microscopy” (American Industrial Hygiene Association Journal, Vol. 63, pp. 756–761), I. Moa et al. reported on determining fiber density by two different methods. T
> There is convincing evidence that breastmilk containing antioxidants is important in the prevention of diseases in infants. Researchers A. Xavier et al. studied the effects of storing breastmilk on antioxidant levels in the article “Total Antioxidant Con
> In the paper “Housing Values Near New Sporting Stadiums” (Land Economics, Vol. 81, Issue 3, pp. 379–395), C. Tu examined the effects of construction of new sports stadiums on home values. Suppose that you want to use a paired sample to decide whether con
> In the paper “An Analysis of Factors That Contribute to the Efficacy of Hypnotic Analgesia” (Journal of Abnormal Psychology, Vol. 96, No. 1, pp. 46–51), D. Price and J. Barber examined the effects of hypnosis on pain. They measured response to pain using
> The article “Accuracy of Self-Reported Height and Weight in a Community-Based Sample of Older African Americans and Whites” (Journal of Gerontology Series A: Biological Sciences and Medical Sciences, Vol. 65A, No. 10, pp. 1123–1129) by G. Fillenbaum et a
> The A. C. Nielsen Company collects data on the TV viewing habits of Americans and publishes the information in Nielsen Report on Television. Suppose that you want to use a paired sample to decide whether the mean viewing times of married men and married
> Provide an example (different from the ones considered in this section) of a procedure based on a paired sample being more appropriate than one based on independent samples.
> Why do you need to know the sampling distribution of the difference between two sample means in order to perform a hypothesis test to compare two population means?
> State the two conditions required for performing a paired t-procedure. How important are those conditions?
> We have drawn a smooth curve that represents a distribution. In each case, do the following: a. Identify the shape of the distribution with regard to modality. b. Identify the shape of the distribution with regard to symmetry (or non-symmetry). c. If the
> What constitutes each pair in a paired sample?
> State one possible advantage of using paired samples instead of independent samples.
> If the assumptions for a non-pooled t-interval are satisfied, the formula for a (1 − α)- level lower confidence bound for the difference, μ1 − μ2, between two population means is For a right-tailed hypothesis test at the significance level α, the null hy
> If the assumptions for a non-pooled t-interval are satisfied, the formula for a (1 − α)- level upper confidence bound for the difference, μ1 − μ2, between two population means is For a left-tailed hypothesis test at the significance level α, the null hyp
> As we mentioned on page 413, the following relationship holds between hypothesis tests and confidence intervals: For a two-tailed hypothesis test at the significance level α, the null hypothesis H0: μ1 = μ2 will be rejected in favor of the alternative hy
> We examine an alternative method, conceived by the late Professor John Tukey, for performing a two-tailed hypothesis test for two population means based on independent random samples. To apply this procedure, one of the samples must contain the largest o
> Suppose that the sample sizes, n1 and n2, are equal for independent simple random samples from two populations. a. Show that the values of the pooled and non-pooled t-statistics will be identical. b. Explain why part (a) does not imply that the two t-tes
> Refer to where each pair of graphs shows the distributions of a variable on two populations. Suppose that, in each case, you want to perform a small-sample hypothesis test based on independent simple random samples to compare the means of the two populat
> Anthropologists are still trying to unravel the mystery of the origins of the Etruscan empire, a highly advanced Italic civilization formed around the eighth century B.C. in central Italy. Were they native to the Italian peninsula or, as many aspects of
> The primary concern is deciding whether the mean of Population 2 differs from the mean of Population 1. a. Determine the null and alternative hypotheses. b. Classify the hypothesis test as two tailed, left tailed, or right tailed.
> We have drawn a smooth curve that represents a distribution. In each case, do the following: a. Identify the shape of the distribution with regard to modality. b. Identify the shape of the distribution with regard to symmetry (or non-symmetry). c. If the
> Suppose that you want to perform a hypothesis test for a population mean based on a small sample but that preliminary data analyses indicate either the presence of outliers or that the variable under consideration is far from normally distributed. a. Is
> What is the difference in assumptions between the one-mean t-test and the one-mean z-test?
> We introduced one-sided one-mean z-intervals. The following relationship holds between hypothesis tests and confidence intervals for one-mean z-procedures: For a right-tailed hypothesis test at the significance level α, the null hypothesis H0: μ = μ0 wil
> We introduced one-sided one-mean z-intervals. The following relationship holds between hypothesis tests and confidence intervals for one-mean z-procedures: For a left-tailed hypothesis test at the significance level α, the null hypothesis H0: μ = μ0 will
> This exercise can be done individually or, better yet, as a class project. For the pretzel-packaging hypothesis test in Example 9.1 on page 352, the null and alternative hypotheses are, respectively, H0: μ = 454 g (machine is working properly) Ha: μ ≠ 45
> The number of cell phone users has increased dramatically since 1987. According to the Semiannual Wireless Survey, published by the Cellular Telecommunications & Internet Association, the mean local monthly bill for cell phone users in the United States
> Data on salaries in the public school system are published annually in Ranking of the States and Estimates of School Statistics by the National Education Association. The mean annual salary of (public) classroom teachers is $55.4 thousand. A random sampl
> A study by researchers at the University of Maryland addressed the question of whether the mean body temperature of humans is 98.6◦F. The results of the study by P. Mackowiak et al. appeared in the article “A Critical Appraisal of 98.6◦F, the Upper Limit
> The daily charges, in dollars, for a sample of 15 hotels and motels operating in South Carolina are provided on the WeissStats site. The data were found in the report South Carolina Statistical Abstract, sponsored by the South Carolina Budget and Control
> We have drawn a smooth curve that represents a distribution. In each case, do the following: a. Identify the shape of the distribution with regard to modality. b. Identify the shape of the distribution with regard to symmetry (or non-symmetry). c. If the
> Answer true or false and explain your answer: If it is important not to reject a true null hypothesis, the hypothesis test should be performed at a small significance level.
> In the article “Business Employment Dynamics: New Data on Gross Job Gains and Losses” (Monthly Labor Review, Vol. 127, Issue 4, pp. 29–42), J. Spletzer et al. examined gross job gains and losses as a percentage of the average of previous and current empl
> A study by M. Chen et al. titled “Heat Stress Evaluation and Worker Fatigue in a Steel Plant” (American Industrial Hygiene Association, Vol. 64, pp. 352–359) assessed fatigue in steelplant workers due to heat stress. A random sample of 29 casting workers
> According to the Bureau of Crime Statistics and Research of Australia, as reported on Lawlink, the mean length of imprisonment for motor-vehicle-theft offenders in Australia is 16.7 months. One hundred randomly selected motor-vehicle-theft offenders in S
> Dementia is the loss of the intellectual and social abilities severe enough to interfere with judgment, behavior, and daily functioning. Alzheimer’s disease is the most common type of dementia. In the article “Living with Early Onset Dementia: Exploring
> Iron is essential to most life forms and to normal human physiology. It is an integral part of many proteins and enzymes that maintain good health. Recommendations for iron are provided in Dietary Reference Intakes, developed by the Institute of Medicine
> The average lactation (nursing) period of all earless seals is 23 days. Grey seals are one of several types of earless seals. The length of time that a female grey seal nurses her pup is studied by S. Twiss et al. in the article “Variation in Female Grey
> Cadmium, a heavy metal, is toxic to animals. Mushrooms, however, are able to absorb and accumulate cadmium at high concentrations. The Czech and Slovak governments have set a safety limit for cadmium in dry vegetables at 0.5 part per million (ppm). M. Me
> We have provided a sample mean, sample size, and population standard deviation. In each case, use the one-mean z-test to perform the required hypothesis test at the 5% significance level. x¯ = 20, n = 24, σ = 4, H0: μ = 22, Ha: μ ≠ 22
> We have provided a sample mean, sample size, and population standard deviation. In each case, use the one-mean z-test to perform the required hypothesis test at the 5% significance level. x¯ = 23, n = 24, σ = 4, H0: μ = 22, Ha: μ ≠ 22
> We have drawn a smooth curve that represents a distribution. In each case, do the following: a. Identify the shape of the distribution with regard to modality. b. Identify the shape of the distribution with regard to symmetry (or non-symmetry). c. If the
> We have provided a sample mean, sample size, and population standard deviation. In each case, use the one-mean z-test to perform the required hypothesis test at the 5% significance level. x¯ = 23, n = 15, σ = 4, H0: μ = 22, Ha: μ > 22
> What is the relation between the significance level of a hypothesis test and the probability of making a Type I error?
> We have provided a sample mean, sample size, and population standard deviation. In each case, use the one-mean z-test to perform the required hypothesis test at the 5% significance level. x¯ = 24, n = 15, σ = 4, H0: μ = 22, Ha: μ > 22
> We have provided a sample mean, sample size, and population standard deviation. In each case, use the one-mean z-test to perform the required hypothesis test at the 5% significance level. x = 21, n = 32, σ = 4, H0: μ = 22, Ha: μ < 22
> We have provided a sample mean, sample size, and population standard deviation. In each case, use the one-mean z-test to perform the required hypothesis test at the 5% significance level. x = 20, n = 32, σ = 4, H0: μ = 22, Ha: μ < 22
> have provided a scenario for a hypothesis test for a population mean. Decide whether the z-test is an appropriate method for conducting the hypothesis test. Assume that the population standard deviation is known in each case. Preliminary data analyses re
> have provided a scenario for a hypothesis test for a population mean. Decide whether the z-test is an appropriate method for conducting the hypothesis test. Assume that the population standard deviation is known in each case. Preliminary data analyses re
> have provided a scenario for a hypothesis test for a population mean. Decide whether the z-test is an appropriate method for conducting the hypothesis test. Assume that the population standard deviation is known in each case. A normal probability plot of
> have provided a scenario for a hypothesis test for a population mean. Decide whether the z-test is an appropriate method for conducting the hypothesis test. Assume that the population standard deviation is known in each case. Preliminary data analyses re
> Explain why considering outliers is important when you are conducting a one-mean z-test.
> We have drawn a smooth curve that represents a distribution. In each case, do the following: a. Identify the shape of the distribution with regard to modality. b. Identify the shape of the distribution with regard to symmetry (or non-symmetry). c. If the
> Let x denote the test statistic for a hypothesis test and x0 its observed value. Then the P-value of the hypothesis test equals a. P(x ≥ x0) for a right-tailed test, b. P(x ≤ x0) for a left-tailed test, c. 2 · min{P(x ≤ x0), P(x ≥ x0)} for a two-tailed t
> The symbol(z) is often used to denote the area under the standard normal curve that lies to the left of a specified value of z. Consider a one-mean z-test. Denote z0 as the observed value of the test statistic z. Express the P-value of the hypothesis tes
> Suppose that, in a hypothesis test, the null hypothesis is in fact false. a. Is it possible to make a Type I error? Explain your answer. b. Is it possible to make a Type II error? Explain your answer.
> Consider a one-mean z-test. Denote z0 as the observed value of the test statistic z. If the test is right tailed, then the P-value can be expressed as P(z ≥ z0). Determine the corresponding expression for the P-value if the test is a. left tailed. b. tw
> We have given the value obtained for the test statistic, z, in a one-mean z-test. We have also specified whether the test is two tailed, left tailed, or right tailed. Determine the P-value in each case and decide whether, at the 5% significance level, th
> We have given the value obtained for the test statistic, z, in a one-mean z-test. We have also specified whether the test is two tailed, left tailed, or right tailed. Determine the P-value in each case and decide whether, at the 5% significance level, th
> We have given the value obtained for the test statistic, z, in a one-mean z-test. We have also specified whether the test is two tailed, left tailed, or right tailed. Determine the P-value in each case and decide whether, at the 5% significance level, th
> We have given the value obtained for the test statistic, z, in a one-mean z-test. We have also specified whether the test is two tailed, left tailed, or right tailed. Determine the P-value in each case and decide whether, at the 5% significance level, th
> We have given the value obtained for the test statistic, z, in a one-mean z-test. We have also specified whether the test is two tailed, left tailed, or right tailed. Determine the P-value in each case and decide whether, at the 5% significance level, th
> We have given the value obtained for the test statistic, z, in a one-mean z-test. We have also specified whether the test is two tailed, left tailed, or right tailed. Determine the P-value in each case and decide whether, at the 5% significance level, th
> We have drawn a smooth curve that represents a distribution. In each case, do the following: a. Identify the shape of the distribution with regard to modality. b. Identify the shape of the distribution with regard to symmetry (or non-symmetry). c. If the
> We have given the P-value for a hypothesis test. Determine the strength of the evidence against the null hypothesis. P = 0.012
> We have given the P-value for a hypothesis test. Determine the strength of the evidence against the null hypothesis. P = 0.001
> We have given the P-value for a hypothesis test. Determine the strength of the evidence against the null hypothesis. P = 0.086
> Suppose that, in a hypothesis test, the null hypothesis is in fact true. a. Is it possible to make a Type I error? Explain your answer. b. Is it possible to make a Type II error? Explain your answer.
> We have given the P-value for a hypothesis test. Determine the strength of the evidence against the null hypothesis. P = 0.184
> We have given the P-value for a hypothesis test. Determine the strength of the evidence against the null hypothesis. P = 0.004
> We have given the P-value for a hypothesis test. Determine the strength of the evidence against the null hypothesis. P = 0.027
> We have given the P-value for a hypothesis test. Determine the strength of the evidence against the null hypothesis. P = 0.35
> We have given the P-value for a hypothesis test. Determine the strength of the evidence against the null hypothesis. P = 0.06
> Which provides stronger evidence against the null hypothesis, a P-value of 0.06 or a P-value of 0.04? Explain your answer.
> We have drawn a smooth curve that represents a distribution. In each case, do the following: a. Identify the shape of the distribution with regard to modality. b. Identify the shape of the distribution with regard to symmetry (or non-symmetry). c. If the
> The document “American Attitudes about Genocide” provided highlights of a nationwide poll with 1000 participants. The survey, conducted by Penn Schoen Berland between June 30 and July 10, 2012, revealed that “66% of respondents believe that genocide is p

