Question: Calcium is the most abundant mineral in
Calcium is the most abundant mineral in the human body and has several important functions. Most body calcium is stored in the bones and teeth, where it functions to support their structure. Recommendations for calcium are provided in Dietary Reference Intakes, developed by the Institute of Medicine of the National Academy of Sciences. The recommended adequate in take (RAI) of calcium for adults (ages 19–50) is 1000 milligrams (mg) per day. A simple random sample of 18 adults with incomes below the poverty level gave the following daily calcium intakes.
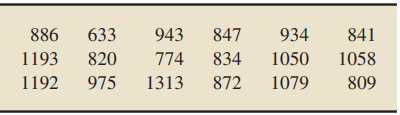
Determine and interpret a 95% confidence interval for the mean calcium intake, μ, of all adults with incomes below the poverty level. Assume that the population standard deviation is 188 mg.
> We have provided a sample mean, sample standard deviation, and sample size. In each case, use the one-mean t -test to perform the required hypothesis test at the 5% significance level. x¯ = 24, s = 4, n = 15, H0: μ = 22, Ha: μ > 22
> We have provided a sample mean, sample standard deviation, and sample size. In each case, use the one-mean t -test to perform the required hypothesis test at the 5% significance level. x¯ = 21, s = 4, n = 32, H0: μ = 22, Ha: μ < 22
> Explain the meaning of Sample distribution.
> We have provided a sample mean, sample standard deviation, and sample size. In each case, use the one-mean t -test to perform the required hypothesis test at the 5% significance level. x¯ = 20, s = 4, n = 32, H0: μ = 22, Ha: μ < 22
> Two-tailed test, n = 8, and t = 3.725 a. Use Table IV in Appendix A to estimate the P-value. b. Based on your estimate in part (a), state at which significance levels the null hypothesis can be rejected, at which significance levels it cannot be rejected
> Two-tailed test, n = 17, and t = −2.733 a. Use Table IV in Appendix A to estimate the P-value. b. Based on your estimate in part (a), state at which significance levels the null hypothesis can be rejected, at which significance levels it cannot be reject
> Left-tailed test, n = 30, and t = −1.572 a. Use Table IV in Appendix A to estimate the P-value. b. Based on your estimate in part (a), state at which significance levels the null hypothesis can be rejected, at which significance levels it cannot be rejec
> Left-tailed test, n = 10, and t = −3.381 a. Use Table IV in Appendix A to estimate the P-value. b. Based on your estimate in part (a), state at which significance levels the null hypothesis can be rejected, at which significance levels it cannot be rejec
> Right-tailed test, n = 11, and t = 1.246 a. Use Table IV in Appendix A to estimate the P-value. b. Based on your estimate in part (a), state at which significance levels the null hypothesis can be rejected, at which significance levels it cannot be rejec
> Right-tailed test, n = 20, and t = 2.235 a. Use Table IV in Appendix A to estimate the P-value. b. Based on your estimate in part (a), state at which significance levels the null hypothesis can be rejected, at which significance levels it cannot be rejec
> Fill in the following blanks. a. The t-test is to moderate violations of the normality assumption. b. The t-test can sometimes be unduly affected by outliers because the sample mean, and sample standard deviation are not to outliers.
> Answer true or false and explain your answer: For a fixed sample size, decreasing the significance level of a hypothesis test results in an increase in the probability of making a Type II error.
> Explain the meaning of the term hypothesis as used in inferential statistics.
> Explain the meaning of Population data.
> A study by researchers at the University of Maryland addressed the question of whether the mean body temperature of humans is 98.6◦F. The results of the study by P. Mackowiak et al. appeared in the article “A Critical Appraisal of 98.6◦F, the Upper Limit
> The U.S. Census Bureau estimates the mean value of the land and buildings per corporate farm. Those estimates are published in the Census of Agriculture. Suppose that an estimate, x¯, is obtained and that the margin of error is $1000. Does this result im
> Professor Thomas Stanley of Georgia State University has surveyed millionaires since 1973. Among other information, Professor Stanley obtains estimates for the mean age, μ, of all U.S. millionaires. Suppose that one year’s study involved a simple random
> Consider again the problem of estimating the mean age, μ, of all people in the civilian labor force. We found that a sample size of 2250 is required to have a margin of error of 0.5 year and a 95% confidence level. Suppose that, due to financial constrai
> Consider again the problem of estimating the mean age, μ, of all people in the civilian labor force. We found that a sample size of 2250 is required to have a margin of error of 0.5 year and a 95% confidence level. Suppose that, due to financial constrai
> According to the document All About Diabetes, found on the website of the American Diabetes Association, “... diabetes is a disease in which the body does not produce or properly use insulin, a hormone that is needed to convert sugar, starches, and other
> The U.S. Department of Justice, Office of Justice Programs, Bureau of Justice Statistics provides information on prison sentences in the document National Corrections Reporting Program. A random sample of 20 maximum sentences for murder yielded the data,
> The Professional Golfer’s Association of America (PGA) organizes golf tournaments for professional golfers. The following table lists the longest drives, in yards, recorded during a PGA tournament for a random sample of 26 golfers. Use the technology of
> Light-emitting diodes (LEDs) and compact fluorescent lights (CFLs) are lightbulbs that are supposed to last up to fifty times longer than old fashioned incandescent lightbulbs and also use less energy. Consumer Reports sampled eighteen different 60-watt
> You found a 99% confidence interval of $2.03 million to $2.51 million for the mean gross earnings of all Rolling Stones concerts. a. Determine the margin of error, E. b. Explain the meaning of E in this context in terms of the accuracy of the estimate. c
> Explain the meaning of Sample data.
> Refer to Exercise 8.7 and find a point estimate for the population standard deviation (i.e., the standard deviation of the variable). Data from Exercise 8.7: A simple random sample is taken from a population and yields the following data for a variable
> You found a 95% confidence interval of 18.8 months to 48.0 months for the mean duration of imprisonment, μ, of all East German political prisoners with chronic PTSD. a. Determine the margin of error, E. b. Explain the meaning of E in this context in term
> You found a 90% confidence interval for the mean number of tongue flicks per 20 minutes for all juvenile common lizards to be from 456.4 to 608.0. Obtain the margin of error by a. taking half the length of the confidence interval. b. using Formula 8.1 on
> You found a 95% confidence interval for the mean amount of all venture-capital investments in the fiber optics business sector to be from $5.389 million to $7.274 million. Obtain the margin of error by: a. taking half the length of the confidence interva
> In estimating the mean monthly fuel expenditure, μ, per household vehicle, the Energy Information Administration takes a sample of size 6841. Assuming that σ = $20.65, determine the margin of error in estimating μ at the 95% level of confidence.
> In the paper “Persistent Pulmonary Hypertension of the Neonate and Asymmetric Growth Restriction” (Obstetrics & Gynecology, Vol. 91, No. 3, pp. 336–341), M. Williams et al. reported on a study of characteristics of neonates. Infants treated for pulmonary
> J. McWhorter et al. of the College of Health Sciences at the University of Nevada, Las Vegas, studied physical therapy students during their graduate-school years. The researchers were interested in the fact that, although graduate physical-therapy stude
> Recall that a simple random sample of 36 new mobile homes yielded the prices, in thousands of dollar. We found the mean of those prices to be $63.28 thousand. a. Use this information and Procedure 8.1 on page 322 to find a 95% confidence interval for the
> Refer to Exercise 8.78. a. The mean duration for a sample of 612 dives was 322 seconds. Find a 99% confidence interval for μ based on that data. b. Compare the 99% confidence intervals obtained here and in Exercise 8.78(b) by drawing a graph. c. Compare
> Refer to Exercise 8.77. a. The mean number of days that 30 adolescents in substance abuse treatment used medical marijuana in the last 6 months was 105.43. Find a 95% confidence interval for μ based on that data. b. Compare the 95% confidence intervals o
> Explain the meaning of Distribution of a data set.
> We presented data on shoe size and height for a sample of students at Arizona State University. Using the regression and correlation techniques that you learned in Chapter 4 and this chapter, solve the following problems. Note: We recommend that you use
> Refer to Exercise 8.78. a. Determine the margin of error for the 95% confidence interval. b. Determine the margin of error for the 99% confidence interval. c. Compare the margins of error found in parts (a) and (b). d. What principle is being illustrated
> A simple random sample is taken from a population and yields the following data for a variable of the population: Find a point estimate for the population mean (i.e., the mean of the variable).
> Refer to Exercise 8.77. a. Determine the margin of error for the 95% confidence interval. b. Determine the margin of error for the 90% confidence interval. c. Compare the margins of error found in parts (a) and (b). d. What principle is being illustrated
> Multi-sensor data loggers were attached to free-ranging American alligators in a study conducted by Y. Watanabe for the article “Behavior of American Alligators Monitored by Multi-Sensor Data Loggers” (Aquatic Biology, Vol. 18, pp. 1–8). The mean duratio
> An issue with legalization of medical marijuana is “diversion,” the process in which medical marijuana prescribed for one person is given, traded, or sold to someone who is not registered for medical marijuana use. Researchers S. Sautel et al. study the
> Refer to Exercise 8.70. a. Find a 90% confidence interval for μ. b. Why is the confidence interval you found in part (a) shorter than the one in Exercise 8.70? c. Draw a graph similar to that shown in Fig. 8.6 on page 326 to display both confidence inter
> Refer to Exercise 8.69. a. Find a 99% confidence interval for μ. b. Why is the confidence interval you found in part (a) longer than the one in Exercise 8.69? c. Draw a graph like that shown in Fig. 8.6 on page 326 to display both confidence intervals. d
> The Rolling Stones, a rock group formed in the 1960s, have toured extensively in support of new albums. Pollstar has collected data on the earnings from the Stones’s North American tours. For 30 randomly selected Rolling Stones concerts, the mean gross e
> A. Ehlers et al. studied various characteristics of political prisoners from the former East Germany and presented their findings in the paper “Posttraumatic Stress Disorder (PTSD) Following Political Imprisonment: The Role of Mental Defeat, Alienation,
> Snakes deposit chemical trails as they travel through their habitats. These trails are often detected and recognized by lizards, which are potential prey. The ability to recognize their predators via tongue flicks can often mean life or death for lizards
> In the special report “Mouse trap: The Most-Visited Shoe and Apparel E-tailers” (Footwear News, Vol. 58, No. 3, p. 18), we found the following data on the average time, in minutes, spent per user per month from January to June of one year for a sample of
> Cadmium, a heavy metal, is toxic to animals. Mushrooms, however, are able to absorb and accumulate cadmium at high concentrations. The Czech and Slovak governments have set a safety limit for cadmium in dry vegetables at 0.5 part per million (ppm). M. Me
> A simple random sample is taken from a population and yields the following data for a variable of the population: Find a point estimate for the population mean (i.e., the mean of the variable).
> Data on investments in the high-tech industry by venture capitalists are compiled by VentureOne Corporation and published in America’s Network Telecom Investor Supplement. A random sample of 18 venture-capital investments in the fiber optics business sec
> x¯ = 55, n = 16, σ = 5, confidence level = 99% a. Use the one-mean z-interval procedure to find a confidence interval for the mean of the population from which the sample was drawn. b. Obtain the margin of error by taking half the length of the confidenc
> x¯ = 50, n = 16, σ = 5, confidence level = 99% a. Use the one-mean z-interval procedure to find a confidence interval for the mean of the population from which the sample was drawn. b. Obtain the margin of error by taking half the length of the confidenc
> x¯ = 35, n = 25, σ = 4, confidence level = 90% a. Use the one-mean z-interval procedure to find a confidence interval for the mean of the population from which the sample was drawn. b. Obtain the margin of error by taking half the length of the confidenc
> x¯ = 30, n = 25, σ = 4, confidence level = 90% a. Use the one-mean z-interval procedure to find a confidence interval for the mean of the population from which the sample was drawn. b. Obtain the margin of error by taking half the length of the confidenc
> x¯ = 25, n = 36, σ = 3, confidence level = 95% a. Use the one-mean z-interval procedure to find a confidence interval for the mean of the population from which the sample was drawn. b. Obtain the margin of error by taking half the length of the confidenc
> x¯ = 20, n = 36, σ = 3, confidence level = 95% a. Use the one-mean z-interval procedure to find a confidence interval for the mean of the population from which the sample was drawn. b. Obtain the margin of error by taking half the length of the confidenc
> The Florida State Center for Health Statistics reported in Women and Cardiovascular Disease Hospitalizations that, for cardiovascular hospitalizations, the mean age of women is 71.9 years. At one hospital, a random sample of 20 female cardiovascular pati
> The margin of error is also called the maximum error of the estimate. Explain why.
> Formula 8.2 provides a method for computing the sample size required to obtain a confidence interval with a specified confidence level and margin of error. The number resulting from the formula should be rounded up to the nearest whole number. a. Why do
> Answer true or false to each statement concerning a confidence interval for a population mean. Give reasons for your answers. The confidence level can be determined if you know only the margin of error, population standard deviation, and sample size.
> Suppose that you take 500 simple random samples from a population and that, for each sample, you obtain a 90% confidence interval for an unknown parameter. Approximately how many of those confidence intervals will not contain the value of the unknown par
> Answer true or false to each statement concerning a confidence interval for a population mean. Give reasons for your answers. The margin of error can be determined if you know only the confidence level, population standard deviation, and sample size.
> Answer true or false to each statement concerning a confidence interval for a population mean. Give reasons for your answers. The confidence level can be determined if you know only the margin of error.
> Answer true or false to each statement concerning a confidence interval for a population mean. Give reasons for your answers. The margin of error can be determined if you know only the confidence level.
> Answer true or false to each statement concerning a confidence interval for a population mean. Give reasons for your answers. The confidence interval can be obtained if you know only the margin of error and the sample mean.
> Answer true or false to each statement concerning a confidence interval for a population mean. Give reasons for your answers. The confidence interval can be obtained if you know only the margin of error.
> Answer true or false to each statement concerning a confidence interval for a population mean. Give reasons for your answers. The margin of error can be determined if you know only the length of the confidence interval.
> Refer to the speed data given in Exercise 2.89. a. Construct a table for the data, based on the classes specified in Exercise 2.89. Interpret your results. b. Construct an ogive for the data. In constructing a stem-and leaf diagram, rounding or truncatin
> Answer true or false to each statement concerning a confidence interval for a population mean. Give reasons for your answers. The length of the confidence interval can be determined if you know only the margin of error.
> A confidence interval for a population mean has a length of 162.6. a. Determine the margin of error. b. If the sample mean is 643.1, determine the confidence interval. c. Construct a graph that illustrates your results.
> A confidence interval for a population mean has length 20. a. Determine the margin of error. b. If the sample mean is 60, obtain the confidence interval. c. Construct a graph that illustrates your results
> A confidence interval for a population mean has a margin of error of 0.047. a. Determine the length of the confidence interval. b. If the sample mean is 0.205, obtain the confidence interval. c. Construct a graph that illustrates your results.
> Suppose that you take 1000 simple random samples from a population and that, for each sample, you obtain a 95% confidence interval for an unknown parameter. Approximately how many of those confidence intervals will contain the value of the unknown parame
> A confidence interval for a population mean has a margin of error of 3.4. a. Determine the length of the confidence interval. b. If the sample mean is 52.8, obtain the confidence interval. c. Construct a graph that illustrates your results.
> Explain the effect on the margin of error and hence the effect on the accuracy of estimating a population mean by a sample mean. Decreasing the sample size while keeping the same confidence Level.
> Explain the effect on the margin of error and hence the effect on the accuracy of estimating a population mean by a sample mean. Increasing the confidence level while keeping the same sample Size.
> Explain the effect on the margin of error and hence the effect on the accuracy of estimating a population mean by a sample mean. Decreasing the confidence level while keeping the same sample size.
> Explain the effect on the margin of error and hence the effect on the accuracy of estimating a population mean by a sample mean. Increasing the sample size while keeping the same confidence level.
> Refer to the energy consumption data given in Exercise 2.84. a. Construct a table similar to Table 2.14 for the data, based on the classes specified in Exercise 2.84. Interpret your results. b. Construct an ogive for the data. Data from Problem 2.84: Us
> Explain why the margin of error determines the accuracy with which a sample mean estimates a population mean.
> Discuss the relationship between the margin of error and the standard error of the mean.
> Suppose that you will be taking a random sample from a population and that you intend to find a 95% confidence interval for the population mean, μ. Which sample size, 25 or 50, will result in the confidence interval giving a more accurate estimate of μ?
> Suppose that you have obtained data by taking a random sample from a population and that you intend to find a confidence interval for the population mean, μ. Which confidence level, 95% or 99%, will result in the confidence interval giving a more accurat
> Suppose that you have obtained data by taking a random sample from a population. Before performing a statistical inference, what should you do?
> Express the form of most of the confidence intervals that you will encounter in your study of statistics in terms of “point estimate” and “margin of error.”
> Assume that the population standard deviation is known and decide whether use of the z-interval procedure to obtain a confidence interval for the population mean is reasonable. Explain your answers. The sample data contain no outliers, the sample size is
> Assume that the population standard deviation is known and decide whether use of the z-interval procedure to obtain a confidence interval for the population mean is reasonable. Explain your answers. The distribution of the variable under consideration is
> Assume that the population standard deviation is known and decide whether use of the z-interval procedure to obtain a confidence interval for the population mean is reasonable. Explain your answers. The sample data contain no outliers, the variable under
> Assume that the population standard deviation is known and decide whether use of the z-interval procedure to obtain a confidence interval for the population mean is reasonable. Explain your answers. The sample data contain outliers, and the sample size i
> As mentioned, for relative-frequency polygons, we label the horizontal axis with class marks in limit grouping and class midpoints in cutpoint grouping. How do you think the horizontal axis is labeled in single-value grouping? Cumulative information can
> Assume that the population standard deviation is known and decide whether use of the z-interval procedure to obtain a confidence interval for the population mean is reasonable. Explain your answers. The variable under consideration is very close to being
> Assume that the population standard deviation is known and decide whether use of the z-interval procedure to obtain a confidence interval for the population mean is reasonable. Explain your answers. The variable under consideration is very close to being
> What is meant by saying that a statistical procedure is robust?
> Refer to Procedure. a. Explain in detail the assumptions required for using the z-interval procedure. b. How important is the normality assumption? Explain your answer.
> For what is normal population an abbreviation?
> In developing Procedure 8.1, we assumed that the variable under consideration is normally distributed. a. Explain why we needed that assumption. b. Explain why the procedure yields an approximately correct confidence interval for large samples, regardles
> When estimating an unknown parameter, what does the margin of error indicate?
> What is meant by saying that a 1 − α confidence interval is a. exact? b. approximately correct?
> Find the confidence level and α for a. an 85% confidence interval. b. a 95% confidence interval.

