Question: Construct the confidence interval for σ21/σ22.
Construct the confidence interval for σ21/σ22. Assume the samples are random and independent, and the populations are normally distributed.
In a recent study of the cholesterol contents of grilled chicken sandwiches served at fast food restaurants, a nutritionist found that random samples of sandwiches from Restaurant A and from Restaurant B had the sample statistics shown in the table. Construct a 95% confidence interval for σ21/σ22, where σ21 and σ22 are the variances of the cholesterol contents of grilled chicken sandwiches from Restaurant A and Restaurant B, respectively.
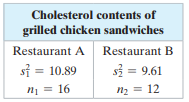
Transcribed Image Text:
Cholesterol contents of grilled chicken sandwiches Restaurant A Restaurant B si = 10.89 s3 = 9.61 n1 = 16 n2 = 12
> Write the claim as a mathematical statement. State the null and alternative hypotheses, and identify which represents the claim. An amusement park claims that the mean daily attendance at the park is at least 20,000 people.
> Write the claim as a mathematical statement. State the null and alternative hypotheses, and identify which represents the claim. The standard deviation of the base price of an all-terrain vehicle is no more than $320.
> Write the claim as a mathematical statement. State the null and alternative hypotheses, and identify which represents the claim. As stated by a company’s shipping department, the number of shipping errors per million shipments has a standard deviation th
> Write the claim as a mathematical statement. State the null and alternative hypotheses, and identify which represents the claim. A tablet manufacturer claims that the mean life of the battery for a certain model of tablet is more than 8 hours.
> Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed. H0: p = 0.25 Ha: p ≠ 0.25
> A null hypothesis is rejected with a level of significance of 0.05. Is it also rejected at a level of significance of 0.10? Explain.
> Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed. H0: σ2 = 142 Ha: σ2 ≠ 142
> Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed. H0: σ ≥ 5.2 Ha: σ < 5.2
> Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed. H0: µ ≤ 8.0 Ha: µ > 8.0
> Match the alternative hypothesis with its graph. Then state the null hypothesis and sketch its graph. Ha: µ > 2 1 1 (d) 1 2
> Match the alternative hypothesis with its graph. Then state the null hypothesis and sketch its graph. Ha: µ ≠3 1 1 (d) 1 2
> Match the alternative hypothesis with its graph. Then state the null hypothesis and sketch its graph. Ha: µ 1 1 (d) 1 2
> Match the alternative hypothesis with its graph. Then state the null hypothesis and sketch its graph. Ha: µ > 3 1 1 (d) 1 2
> The statement represents a claim. Write its complement and state which is H0 and which is Ha. p = 0.21
> The statement represents a claim. Write its complement and state which is H0 and which is Ha. p < 0.45
> The statement represents a claim. Write its complement and state which is H0 and which is Ha. σ2 ≥ 1.2
> Explain why a level of significance of α = 0 is not used.
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> Describe the hypotheses for a two-way ANOVA test.
> Describe the difference between the variance between samples MSB and the variance within samples MSW.
> Refer to the data in Exercise 11. At α = 0.10, perform a Scheffé Test to determine which means have a significant difference. From Exercise 11: The well-being index is a way to measure how people are faring physically, emotion
> Refer to the data in Exercise 8. At α = 0.01, perform a Scheffé Test to determine which means have a significant difference. From Exercise 8: The table shows the salaries (in thousands of dollars) for a sample of individuals f
> Refer to the data in Exercise 7. At α = 0.01, perform a Scheffé Test to determine which means have a significant difference. From Exercise 7: The table shows the weights (in pounds) for a sample of vacuum cleaners. The weights
> Why can decreasing the probability of a type I error cause an increase in the probability of a type II error?
> What conditions are necessary in order to use a one-way ANOVA test?
> Refer to the data in Exercise 5. At α = 0.05, perform a Scheffé Test to determine which means have a significant difference. From Exercise 5: The table shows the costs per ounce (in dollars) for a sample of toothpastes exhibit
> Use technology and the block design to perform a two-way ANOVA test. Use α = 0.10. Interpret the results. Assume the samples are random and independent, the populations are normally distributed, and the population variances are equal. The m
> Use technology and the block design to perform a two-way ANOVA test. Use α = 0.10. Interpret the results. Assume the samples are random and independent, the populations are normally distributed, and the population variances are equal. A stu
> Use technology and the block design to perform a two-way ANOVA test. Use α = 0.10. Interpret the results. Assume the samples are random and independent, the populations are normally distributed, and the population variances are equal. The o
> Use technology and the block design to perform a two-way ANOVA test. Use α = 0.10. Interpret the results. Assume the samples are random and independent, the populations are normally distributed, and the population variances are equal. A stu
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> An Internet provider is trying to gain advertising deals and claims that the mean time a customer spends online per day is greater than 28 minutes. You are asked to test this claim. How would you write the null and alternative hypotheses when a. you rep
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> State the null and alternative hypotheses for a one-way ANOVA test.
> Find the critical F-value for a two-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D. α = 0.01, d.f.N = 6, d.f.D = 7
> Find the critical F-value for a right-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D. α = 0.025, d.f.N = 7, d.f.D = 3
> Find the critical F-value for a right-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D. α = 0.10, d.f.N = 10, d.f.D = 15
> Find the critical F-value for a right-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D. α = 0.01, d.f.N = 2, d.f.D = 11
> Find the critical F-value for a right-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D. α = 0.05, d.f.N = 9, d.f.D = 16
> Explain how to determine the values of d.f.N and d.f.D when performing a two-sample F-test.
> Construct the confidence interval for σ21/σ22. Assume the samples are random and independent, and the populations are normally distributed. In a recent study of the carbohydrate contents of grilled chicken sandwiches served at fast
> List the three conditions that must be met in order to use a two-sample F-test.
> A backpack manufacturer claims that the mean life of its competitor’s backpacks is less than 5 years. You are asked to perform a hypothesis test to test this claim. How would you write the null and alternative hypotheses when a. you represent the manufa
> Find the right- and left-tailed critical F-values for a two-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D. α = 0.10, d.f.N = 20, d.f.D = 15
> Find the right- and left-tailed critical F-values for a two-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D. α = 0.05, d.f.N = 6, d.f.D = 3
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> A transportation network company claims that the mean travel time between two destinations is about 16 minutes. You work for one of the company’s competitors and want to reject this claim. How would you write the null and alternative hypotheses?
> a. Identify the claim and state H0 and Ha. b. Determine whether the hypothesis test is left-tailed, right-tailed, or two-tailed, and whether to use a z-test, a t-test, or a chi-square test. Explain your reasoning. c. Choose one of the options. Option
> List five properties of the F-distribution.
> a. identify the claim and state H0 and Ha, b. find the critical value and identify the rejection region, c. find the test statistic F, d. decide whether to reject or fail to reject the null hypothesis, and e. interpret the decision in the context of
> Test the claim about the difference between two population variances σ21 and σ22 at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed. Claim: σ21 > σ22; α = 0.05. Sample statistics: s
> Test the claim about the difference between two population variances σ21 and σ22 at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed. Claim: σ21 = σ22; α = 0.01. Sample statistics: s
> Test the claim about the difference between two population variances σ21 and σ22 at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed. Claim: σ21 ≠ σ22; α = 0.05. Sample statistics: s
> Test the claim about the difference between two population variances σ21 and σ22 at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed. Claim: σ21 ≤ σ22; α = 0.01. Sample statistics: s
> Test the claim about the difference between two population variances σ21 and σ22 at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed. Claim: σ21 = σ22; α = 0.05. Sample statistics: s
> Test the claim about the difference between two population variances σ21 and σ22 at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed. Claim: σ21 > σ22; α = 0.10. Sample statistics: s
> Find the critical F-value for a two-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D. α = 0.05, d.f.N = 27, d.f.D = 19
> Find the critical F-value for a two-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D. α = 0.05, d.f.N = 60, d.f.D = 40
> A medical research team is investigating the mean cost of a 30-day supply of a heart medication. A pharmaceutical company thinks that the mean cost is less than $60. You want to support this claim. How would you write the null and alternative hypotheses?
> Find the critical F-value for a two-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D. α = 0.10, d.f.N = 24, d.f.D = 28
> Explain how to find the critical value for an F-test.
> a. calculate the marginal frequencies and b. find the expected frequency for each cell in the contingency table. Assume that the variables are independent. Preference Bank employee New procedure Old procedure No preference Teller 92 351 50 Customer
> a. calculate the marginal frequencies and b. find the expected frequency for each cell in the contingency table. Assume that the variables are independent. Treatment Result Drug Placebo Nausea 36 13 No nausea 254 262
> a. calculate the marginal frequencies and b. find the expected frequency for each cell in the contingency table. Assume that the variables are independent. Athlete has Result Stretched Not stretched Injury No injury 18 22 211 189
> Determine whether the statement is true or false. If it is false, rewrite it as a true statement. When the test statistic for the chi-square independence test is large, you will, in most cases, reject the null hypothesis.
> Determine whether the statement is true or false. If it is false, rewrite it as a true statement. If the two variables in a chi-square independence test are dependent, then you can expect little difference between the observed frequencies and the expecte
> Use the contingency table from Exercises 33–36, and the information below. From Exercises 33–36: What percent of U.S. adults ages 25 and over who are not high school graduates are unemployed? Educational attainme
> Use the contingency table from Exercises 33–36, and the information below. From Exercises 33–36: What percent of U.S. adults ages 25 and over who have a degree are not in the labor force? Educational attainment A
> Use the contingency table from Exercises 33–36, and the information below. From Exercises 33–36: Calculate the conditional relative frequencies in the contingency table based on the column totals. Educational att
> Determine whether the claim represents the null hypothesis or the alternative hypothesis. If a hypothesis test is performed, how should you interpret a decision that a. rejects the null hypothesis? b. fails to reject the null hypothesis? A marketing or
> Explain why the chi-square independence test is always a right-tailed test.
> Use the contingency table from Exercises 33–36, and the information below. From Exercises 33–36: What percent of U.S. adults ages 25 and over who are not in the labor force have some college education, but no degree?
> Use the contingency table from Exercises 33–36, and the information below. From Exercises 33–36: What percent of U.S. adults ages 25 and over who are employed have a degree? Educational attainment Associate's, No
> Use the contingency table from Exercises 33–36, and the information below. From Exercises 33–36: Calculate the conditional relative frequencies in the contingency table based on the row totals. Educational attain
> Use the information below. The frequencies in a contingency table can be written as relative frequencies by dividing each frequency by the sample size. The contingency table below shows the number of U.S. adults (in millions) ages 25 and over by employm
> Use the information below. The frequencies in a contingency table can be written as relative frequencies by dividing each frequency by the sample size. The contingency table below shows the number of U.S. adults (in millions) ages 25 and over by employm
> Use the information below. The frequencies in a contingency table can be written as relative frequencies by dividing each frequency by the sample size. The contingency table below shows the number of U.S. adults (in millions) ages 25 and over by employm
> Use the information below. The frequencies in a contingency table can be written as relative frequencies by dividing each frequency by the sample size. The contingency table below shows the number of U.S. adults (in millions) ages 25 and over by employm
> Use this information about the homogeneity of proportions test. Another chi-square test that involves a contingency table is the homogeneity of proportions test. This test is used to determine whether several proportions are equal when samples are taken
> Use this information about the homogeneity of proportions test. Another chi-square test that involves a contingency table is the homogeneity of proportions test. This test is used to determine whether several proportions are equal when samples are taken
> Determine whether the claim represents the null hypothesis or the alternative hypothesis. If a hypothesis test is performed, how should you interpret a decision that a. rejects the null hypothesis? b. fails to reject the null hypothesis? A report claim
> Use this information about the homogeneity of proportions test. Another chi-square test that involves a contingency table is the homogeneity of proportions test. This test is used to determine whether several proportions are equal when samples are taken
> Explain how the chi-square independence test and the chi-square goodness-of-fit test are similar. How are they different?
> Perform the indicated chi-square independence test by performing the steps below. a. Identify the claim and state H0 and Ha. b. Determine the degrees of freedom, find the critical value, and identify the rejection region. c. Find the chi-square test s
> Perform the indicated chi-square independence test by performing the steps below. a. Identify the claim and state H0 and Ha. b. Determine the degrees of freedom, find the critical value, and identify the rejection region. c. Find the chi-square test s
> Determine whether the claim represents the null hypothesis or the alternative hypothesis. If a hypothesis test is performed, how should you interpret a decision that a. rejects the null hypothesis? b. fails to reject the null hypothesis? An automotive
> Perform the indicated chi-square independence test by performing the steps below. a. Identify the claim and state H0 and Ha. b. Determine the degrees of freedom, find the critical value, and identify the rejection region. c. Find the chi-square test s
> Perform the indicated chi-square independence test by performing the steps below. a. Identify the claim and state H0 and Ha. b. Determine the degrees of freedom, find the critical value, and identify the rejection region. c. Find the chi-square test s

