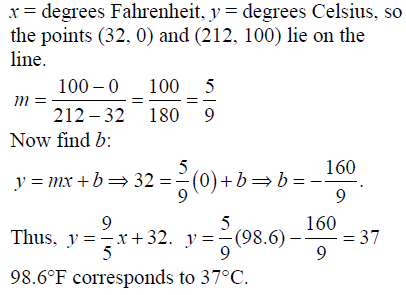
[SOLVED] Decide which curves are graphs of functions. /

> Consider the rectangle in Exercise 1. Write an expression for the perimeter. If the area is 25 square feet, write this fact as an equation. y = -x - y = x² a

> Assign variables to the dimensions of the geometric object. y = x2 y = 2x – 1 a

> Let f (x) = x / x - 2, g(x) = 5 – x / 5 + x, and h(x) = x + 1 / 3x - 1. Express the following as rational functions. f (x + 2) + g(x + 2)

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. (16x8)-3/4

> An office supply firm finds that the number of laptop computers sold in year x is given approximately by the function f (x) = 150 + 2x + x2, where x = 0 corresponds to 2015. (a) What does f (0) represent? (b) Find the number of laptops sold in 2020.

> Compute the numbers. 1100

> Let f (x) = x / x - 2, g(x) = 5 – x / 5 + x, and h(x) = x + 1 / 3x - 1. Express the following as rational functions. g(x)h(x)

> Let f (x) = x2 - 2x + 4, g(x) = 1/x2, and h(x) = 1/(√x - 1). Determine the following functions. f (g(x))

> Compute the numbers. (-2)3

> Compute the numbers. 33

> Convert the numbers from graphing calculator form to standard form (that is, without E). 8.23E-6

> Convert the numbers from graphing calculator form to standard form (that is, without E). 1.35E13

> Refer to the cost function in Fig. 18. Translate the task âfind C(400)â into a task involving the graph. Vx for 0<x < 2 f (x) = - |1+x for 2 <x<5 f(1) = Vĩ = 1 f(2) = 1+2 = 3 f (3) = 1+3 = 4

> Convert the numbers from graphing calculator form to standard form (that is, without E). 8.103E-4

> Convert the numbers from graphing calculator form to standard form (that is, without E). 5E-5

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. 1 / yx-5

> Velocity When a car’s brakes are slammed on at a speed of x miles per hour, the stopping distance is 1 20x2 feet. Show that when the speed is doubled the stopping distance increases fourfold.

> Let f (x) = x6, g(x) = x / 1 - x, and h(x) = x3 - 5x2 + 1. Calculate the following functions. h (f (t))

> Draw the following intervals on the number line. (4, 3π)

> Semiannual Compound Assume that a $1000 investment earns interest compounded semiannually. Express the value of the investment after 2 years as a polynomial in the annual rate of interest r.

> Assume that a $500 investment earns interest compounded quarterly. Express the value of the investment after 1 year as a polynomial in the annual rate of interest r.

> Use intervals to describe the real numbers satisfying the inequalities. x ≥ 12

> Assume that a couple invests $4000 each year for 4 years in an investment that earns 8% compounded annually. What will the value of the investment be 8 years after the first amount is invested?

> Assume that a couple invests $1000 upon the birth of their daughter. Assume that the investment earns 6.8% compounded annually. What will the investment be worth on the daughter’s 18th birthday?

> Refer to the cost function in Fig. 18. Translate the task âsolve C(x) = 3500 for xâ into a task involving the graph of the function. C D B E A Figure 12

> If the cylinder in Exercise 6 has a volume of 54p cubic inches, find the surface area of the cylinder. Cylinder in Exercise 6: C D B E A Figure 12

> Calculate the compound amount from the given data. principal = $1500, compounded daily, 3 years, annual rate = 6%

> Calculate the compound amount from the given data. principal = $1500, compounded daily,1 year, annual rate = 6%

> Describe the domain of the function. f (x) =8x / (x - 1)(x - 2)

> Decide which curves are graphs of functions. 8 7 6 3 2 1 2 3 4 5 6 7 8 4) 1.

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. 2x / √x

> Calculate the compound amount from the given data. principal = $500, compounded monthly,1 year, annual rate = 4.5%

> Calculate the compound amount from the given data. principal = $100, compounded monthly, 10 years, annual rate = 5%

> In Exercises 47–50, find the zeros of the function. (Use the specified viewing window.) f (x) = x2 - x - 2; [-4, 5] [-4, 10]

> Calculate the compound amount from the given data. principal = $20,000, compounded quarterly, 3 years, annual rate = 12%

> Calculate the compound amount from the given data. principal = $50,000, compounded quarterly, 10 years, annual rate = 9.5%

> Calculate the compound amount from the given data. principal = $700, compounded annually, 8 years, annual rate = 8%

> In Exercises 51–54, find the points of intersection of the graphs of the functions. (Use the specified viewing window.) f (x) = 2x - 1; g(x) = x2 - 2; [-4, 4] by [-6, 10]

> Let f (x) = x / x - 2, g(x) = 5 – x / 5 + x, and h(x) = x + 1 / 3x - 1. Express the following as rational functions. f (x)g(x)

> Let f (x) = x/(x2 - 1), g(x) = (1 - x)/(1 + x), and h(x) = 2/(3x + 1). Express the following as rational functions. f (x) + g(x)

> A catering company estimates that, if it has x customers in a typical week, its expenses will be approximately C(x) = 550x + 6500 dollars, and its revenue will be approximately R(x) = 1200x dollars. (a) How much profit will the company earn in 1 week whe

> Calculate the compound amount from the given data. principal = $500, compounded annually, 6 years, annual rate = 6%

> Evaluate f (4). f (x) = x0

> Evaluate f (4). f (x) = x-5/2

> Sketch the graph of the function. f (x) = √(x + 1)

> Evaluate f (4). f (x) = x-1/2

> Evaluate f (4). f (x) = x3/2

> When a car is moving at x miles per hour and the driver decides to slam on the brakes, the car will travel x + (1/20) x2 feet. (The general formula is f (x) = ax + bx2, where the constant a depends on the driver’s reaction time and the constant b depends

> Draw the following intervals on the number line. [ -2, √2)

> Let f (x) = x/(x2 - 1), g(x) = (1 - x)/(1 + x), and h(x) = 2/(3x + 1). Express the following as rational functions. g(x) - h(x - 3)

> Evaluate f (4). f (x) = x1/2

> Evaluate f (4). f (x) = x-1

> Evaluate f (4). f (x) = x3

> Let f (x) = x / x - 2, g(x) = 5 – x / 5 + x, and h(x) = x + 1 / 3x - 1. Express the following as rational functions. f (t) - h(t)

> Evaluate f (4). f (x) = x2

> In Exercises 7–12, express f (x) + g(x) as a rational function. Carry out all multiplications. f (x) = x + 5 / x – 10, g(x) = x / x + 10

> The expressions in Exercises 83–88 may be factored as shown. Find the missing factors. Explain why √a/√b = √ (a/b).

> The expressions in Exercises 83–88 may be factored as shown. Find the missing factors. Explain why √a * √b = √(ab).

> The expressions in Exercises 83–88 may be factored as shown. Find the missing factors. √ (x/y) - √ (y/x) = √xy ( )

> The expressions in Exercises 83–88 may be factored as shown. Find the missing factors. x-1/4 + 6x1/4 = x-1/4( )

> Let f (x) = 3√x and g(x) = 1 / x2. Calculate the following functions. Take x > 0. [ f (x)]3g(x)

> Graph the following equations. y = 3x + 1

> The expressions in Exercises 83–88 may be factored as shown. Find the missing factors. 2x2/3 - x-1/3 = x-1/3 ( )

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. (3x2 / 2y)3

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. (x)3/2 * (x)2/3

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. (-3x)3

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. x-4 / x3

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. x3 / y-2

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. -x3y / -xy

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. -3x / 15x4

> Refer to the cost and revenue functions in Fig. 17. The cost of producing x units of goods is C(x) dollars and the revenue from selling x units of goods is R(x) dollars. At what level of production is the cost $1400? 1 x+ 2y = 0= y = --x= m = 2 1 2

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. (2x)4

> In Exercises 7–12, express f (x) + g(x) as a rational function. Carry out all multiplications. f (x) =-x / x + 3, g(x) = x / x + 5

> The expressions in Exercises 83–88 may be factored as shown. Find the missing factors. √x – 1/√x = 1/√x ( )

> Solve the equations in Exercises 39–44. 1 = 5 / x +6 / x2

> Sketch the graph of the function. f (x) = 2x2 - 1

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. x-3 * x7

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. x5 * (y2 / x)3

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. √(1 + x) * (1 + x)3/2

> Let f (x) = x/(x2 - 1), g(x) = (1 - x)/(1 + x), and h(x) = 2/(3x + 1). Express the following as rational functions. f (x) + h(x)

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. (x3y5)4

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. (x/y)-2

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. (x4 / y2)3

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. (x3 * y6)1/3

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. x-1/2

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. 1/x-3

> Solve the equations in Exercises 39–44. x + 14 / x + 4 = 5

> In Exercises 7–12, express f (x) + g(x) as a rational function. Carry out all multiplications. f (x) = x / x - 8, g(x) =-x / x - 4

> Let f (x) = x/(x2 - 1), g(x) = (1 - x)/(1 + x), and h(x) = 2/(3x + 1). Express the following as rational functions. g(x) - h(x)

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. (x4 * y5)/ xy2

> Sketch the graph of the function. f (x) = x2 + 1

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. (x1/3)6

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. (-27x5)2/3 / x3/2

> Use the laws of exponents to simplify the algebraic expressions. Your answer should not involve parentheses or negative exponents. (xy)6

> Use the laws of exponents to compute the numbers. (61/2)0

> Use the laws of exponents to compute the numbers. 74/3 / 71/3

> Use the laws of exponents to compute the numbers. (125 * 27)1/3

> Let f (x) = 3√x and g(x) = 1 / x2. Calculate the following functions. Take x > 0. g(g(x))

> Use the laws of exponents to compute the numbers. (8/27)2/3

Question: Decide which curves are graphs of functions. /

Transcribed Image Text: