Question: Determine whether each integral is convergent or
Determine whether each integral is convergent or divergent. Evaluate those that are convergent.
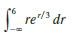
Transcribed Image Text:
9. re dr
> Sketch the region that lies between the curves y = cos x and y = sin 2x and between x = 0 and x = π/2. Notice that the region consists of two separate parts. Find the area of this region.
> Show that f10(1 – x2) n dx = 22n(n!)2/ (2n + 1)! Hint: Start by showing that if denotes the integral, then 2k + 2 - Ik 2k + 3 Ik+1
> Use a graph to find approximate x-coordinates of the points of intersection of the given curves. Then find (approximately) the area of the region bounded by the curves. y = x cos x, y=x10
> Use a graph to find approximate x-coordinates of the points of intersection of the given curves. Then find (approximately) the area of the region bounded by the curves. y = x² In x, y = VI – I (х — 1
> Use a graph to find approximate x-coordinates of the points of intersection of the given curves. Then find (approximately) the area of the region bounded by the curves. y = y = x* – x, x 0 (x² + 1)*"
> A high-speed bullet train accelerates and decelerates at the rate of 4ft/s2. Its maximum cruising speed is 90 mi/h. (a). What is the maximum distance the train can travel if it accelerates from rest until it reaches its cruising speed and then runs at th
> Find the area of the shaded region. y. y = Vx+2 x= 2 1 х+1
> Use a graph to find approximate x-coordinates of the points of intersection of the given curves. Then find (approximately) the area of the region bounded by the curves. y = x sin(x²), y = x*
> Sketch the region enclosed by the given curves and find its area. y = 3x², y= 8r², 4x + y = 4, x> 0 %3D
> Sketch the region enclosed by the given curves and find its area. y = 1/x, y= x, y=}x, x>0
> Sketch the region enclosed by the given curves and find its area. у %3D сos x, у — 2 — cos x, 0x<2п
> Sketch the region enclosed by the given curves and find its area. y = e", y = xe", x= 0
> A hemispherical bubble is placed on a spherical bubble of radius 1. A smaller hemispherical bubble is then placed on the first one. This process is continued until chambers, including the sphere, are formed. (The figure shows the case n = 4.) Use mathema
> Sketch the region enclosed by the given curves and find its area. y = x', y = 4x – x?
> Sketch the region enclosed by the given curves and find its area. у — 12 — х', у-х*— 6 y= x² – 6
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. у %3 sin x, у— 2х/т, х>0
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. x= 2y', x= 4 + y? %3D
> To prove Theorem 1, let F and G be any two antiderivatives of f on I and let H = G - F. (a). If x1 and x2 are any two numbers in I with x1 < x2, apply the Mean Value Theorem on the interval [x1, x2] to show that H (x1) = H (x2). Why does this show that H
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. 4x + y? = 12, x= y
> Find the area of the shaded region. yA y = 5x – x? ((4, 4) y=x
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. -/2 e dy
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. J. Tr? + 2)²
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. -1 dw 2 –
> In an automobile race along a straight road, car A passed car B twice. Prove that at some time during the race their accelerations were equal.
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1 dx V1 +x 4.
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1 (x – 2)2
> Show that ½ (Tn + Mn) = T2n.
> (a). Graph the functions f (x) = 1/x1.1 and g (x) = 1/x0.9 in the viewing rectangles [0, 10] by [0, 1] and [0, 100] by [0, 1]. (b). Find the areas under the graphs of f and g from x = 1 to x = t and evaluate for t =10, 100, 104, 106, 1010, and 1020. (c).
> Sketch the region and find its area (if the area is finite). s = {(x, y) | x > -2, 0 < y<e?}
> If the units for are feet and the units for a (x) are pounds per foot, what are the units for da/dx? What units does f82 a(x) dx have?
> Sketch the region and find its area (if the area is finite). S = {(r, y) | x < 1, 0 < y< e*}
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. In x dx
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. *2 (2' In z dz Jo
> Find the area under the curve y = 1/x3 from x = 1 to x = t and evaluate it for t = 10, 100, and 1000. Then find the total area under this curve for x > 1.
> Find the minimum value of the area of the region under the curve y = x + 1/x from x = a to x = a + 1.5, for all a > 0.
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 33 " (x – 1)-1/5 dx
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. хр (х — 6)° J6 4.
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. *14 dx -2 x + 2
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 3 dx
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. dx. e2* + 3
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. Je x(In x)
> If x is measured in meters and f (x) is measured in newtons, what are the units for f0100 f (x) dx?
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. In x dx .3
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. x? dx 9 + x*
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. x'e dx
> The line y = mx + b intersects the parabola y = x2 in points A and B. (See the figure.) Find the point P on the arc AOB of the parabola that maximizes the area of the triangle PAB. y y =x B y = mx +b P
> (a). The base of a solid is a square with vertices located at (1, 0), (0, 1) and (0, -1). Each cross-section perpendicular to the x-axis is a semicircle. Find the volume of the solid. (b). Show that by cutting the solid of part (a), we can rearrange it t
> Which of the following integrals are improper? Why? (a) f dx. 2x - 1 (b) Jo 2x 1 dx :- 1 sin x dx -1+x* (d) * In(x – 1) dx
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. In x dx
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. se-* ds -5s Jo
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. * cos at dt
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. x +1 - dx x? + 2x
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. dx
> Since raindrops grow as they fall, their surface area increases and therefore the resistance to their falling increases. A raindrop has an initial downward velocity of 10 m/s and its downward acceleration is If the raindrop is initially 500 m above the
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. xedx
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. L – 3y°) dy
> Use an integral to estimate the sum ∑(i=1)^1000 √i.
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. sin e de
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. -1 -21 dt
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. | tan'(7x) dx TX
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) In x -dx, п 3D 10 dx, n= 1 +х
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) *1/2 sin(r*) dx, n= 4
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) 1 + x² dx, n = 8
> A bacteria population starts with 400 bacteria and grows at a rate of r (t) = (450.268) e1.12567t bacteria per hour. How many bacteria will there be after three hours?
> An oil storage tank ruptures at time t = 0 and oil leaks from the tank at a rate of r (t) = 100e-0.01t liters per minute. How much oil leaks out during the first hour?
> A manufacturer of lightbulbs wants to produce bulbs that last about 700 hours but, of course, some bulbs burn out faster than others. Let F (t) be the fraction of the company’s bulbs that burn out before t hours, so F (t) always lies be
> (a). If f (x) = ln x, 1 < x < 4, use the commands discussed in Exercise 9 to find the left and right sums for n = 10, 30, and 50. Exercise 9: Some computer algebra systems have commands that will draw approximating rectangles and evaluate the sums of t
> If P (a, a2) is any point on the parabola y = x2, except for the origin, let Q be the point where the normal line intersects the parabola again. Show that the line segment PQ has the shortest possible length when a = 1/√2. y P
> A model for the basal metabolism rate, in kcal/h, of a young man is R (t) = 85 – 0.18 cos (πt/12), where t is the time in hours measured from 5:00 AM. What is the total basal metabolism of this man, f240 R (t) dt, over a 24-hour time period?
> Which of the following areas are equal? Why? yA y y = 2xe" y y= ein x sin 2.r
> Evaluate f10 x√1 – x4, dx by making a substitution and interpreting the resulting integral in terms of an area.
> Use (a) the Midpoint Rule and (b) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) Compare your results to the actual value to determine the error in each approx
> Evaluate f2-2 (x + 3) √4 – x2, dx by writing it as a sum of two integrals and interpreting one of those integrals in terms of an area.
> Verify that f (x) = sin 3√x is an odd function and use that fact to show that <L, sin ī dx < 1
> Evaluate the definite integral. f10 dx/ (1 + √x)4
> Evaluate the definite integral. fπ/20 sin (2πt/T – a) dt
> Evaluate the definite integral. f1/20 sin-1 x/√1 – x2, dx
> Evaluate the definite integral. f10 ez + 1/ez – 1, dz
> Sketch the set of all points (x, y) such that |x + y| < ex.
> Suppose that a region R has area A and lies above the x-axis. When R is rotated about the x-axis, it sweeps out a solid with volume V1. When R is rotated about the line y = -k (where k is a positive number), it sweeps out a solid with volume V2. Express
> Evaluate the definite integral. f21 x √x – 1, dx
> Evaluate the definite integral. fπ/2-π/2 x2 sin x/1 + x6, dx
> Use (a) the Midpoint Rule and (b) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) Compare your results to the actual value to determine the error in each approx
> Evaluate the definite integral. fπ/4-π/4 (x3 + x4 tan x) dx
> Evaluate the definite integral. fπ/20 cos x sin (sin x) dx
> If f (0) = g (0) = 0 and f" and g" are continuous, show that fWg"(x) dx = f(a)g'(a) – f'(a)gla) + {" f"()g(1) dx
> (a). Use integration by parts to show that f f (x) dx = xf (x) – f xf'(x) dx (b). If f and g are inverse functions and f' is continuous, prove that [Hint: Use part (a) and make the substitution y = f (x)] (c). In the case where f and
> Suppose that f (1) = 2, f (4) = 7, f'(1) = 5, f'(4) = 3, and f" is continuous. Find the value of f41 x f"(x) dx.
> A rocket accelerates by burning its onboard fuel, so its mass decreases with time. Suppose the initial mass of the rocket at liftoff (including its fuel) is m, the fuel is consumed at rate r, and the exhaust gases are ejected with constant velocity ve (r
> Solve Exercise 20 if the tank is half full of oil that has a density of 900 kg/m3. Exercise 20: A tank is full of water. Find the work required to pump the water out of the spout. In Exercises 21 and 22 use the fact that water weighs 62.5 lb/ft3.
> A particle that moves along a straight line has velocity v (t) = t2e-t meters per second after seconds. How far will it travel during the first seconds?
> Some of the pioneers of calculus, such as Kepler and Newton, were inspired by the problem of finding the volumes of wine barrels. (In fact, Kepler published a book Stereometria doliorum in 1615 devoted to methods for finding the volumes of barrels.) They
> Use integration by parts to prove the reduction formula. f xn ex dx = xn ex – n f xn-1 ex dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. 1 dx x?/4x? – 7
> Use integration by parts to prove the reduction formula. f (ln x) n dx = x (ln x) n – n f (ln x) n-1 dx
> Use the Trapezoidal Rule with n = 10 to approximate f200 cos (πx) dx. Compare your result to the actual value. Can you explain the discrepancy?
> Sketch the graph of a continuous function on [0, 2] for which the Trapezoidal Rule with n = 2 is more accurate than the Midpoint Rule.
> Sketch the graph of a continuous function on [0, 2] for which the right endpoint approximation with n = 2 is more accurate than Simpson’s Rule.
> The intensity of light with wavelength traveling through a diffraction grating with N slits at an angle θ is given by I (θ) = N2 sin2k/k2, where k = (πNd sin θ)/λ and d is the distance between adjacent slits. A helium-neon laser with wavelength λ = 632.8
> The figure shows a pendulum with length L that makes a maximum angle θ0 with the vertical. Using Newton’s Second Law, it can be shown that the period T (the time for one complete swing) is given by where k = sin (1/2&Icir

