Question: Determine whether the sequence converges or
Determine whether the sequence converges or diverges. If it converges, find the limit.
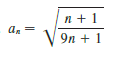
Transcribed Image Text:
n + 1 an 9n + 1
> What are at least three explanations of ADHD?
> Explain how Moffitt’s original dichotomy of juvenile offending has been modified in recent years.
> Discuss reasons why juveniles as a group may be especially susceptible to waiving their constitutional rights and to making false confessions.
> In the Scrivner study, what five different officer profiles were prone to excessive force complaints?
> Debate the pros and cons of EBP with several classmates. Why would a focus on EBP be good for nursing? What are some drawbacks?
> Following the example of CRNA student Maria in the opening case study, outline a potential research study using one of the theories or models presented in this chapter as a framework as depicted in the opening case study. Show how the model or theory can
> Examine early issues of American Journal of Nursing (1900–1950). Determine if and how theories were used in nursing practice. What types of theories were used? Review current issues to analyze how this has changed.
> Consider the following case: A 30-year-old woman arrives in the emergency department. She is diagnosed with a drug overdose. Assessment data reveal the following information: she has three children (18 months, 4 years old, and 14 years old); she is in th
> Select one of the middle range theories derived from a grand nursing theory and one derived from a non-nursing theory. Analyze both for ease of application to research and practice.
> Choose one of the models discussed in this chapter and demonstrate its use in the care of a selected client. Write a nursing care plan using the model. Define all elements of the nursing care plan using the language and the assumptions/propositions of th
> Find an example of a middle range nursing theory (see Chapter 10 or 11 for ideas). Following the preceding exemplar, identify the components of the theory (e.g., scope of the theory, purpose, concepts, and definitions).
> Find an example of a nursing theory in a current book or periodical. Review the theory and classify it based on scope or level of abstraction (grand theory, middle range theory, or practice theory), the purpose of the theory (describe, explain, predict,
> Discuss the use of patient simulators in clinical nursing staff education. Consider the cost and upkeep of the equipment for simulators and faculty training and education and the need for technical support of the equipment.
> Find reports that present middle range or practice theories in the nursing literature. Identify if these theories are descriptive, explanatory, predictive, or prescriptive in nature.
> Does categorizing or classifying grand theories as the writers have done assist in studying and understanding them? Why or why not?
> Find a formula for the general term an of the sequence, assuming that the pattern of the first few terms continues.
> Find a formula for the general term an of the sequence, assuming that the pattern of the first few terms continues. 1 2 4: 9 3 4 16 25 ...)
> Find a formula for the general term an of the sequence, assuming that the pattern of the first few terms continues. {2, 7, 12, 17, ...}
> Find a formula for the general term an of the sequence, assuming that the pattern of the first few terms continues. {1,5,3... 1 1 1 1 3. 9, : • 27 81 27. 8I {
> (a). Let a1 = a, a2 = f (a), a3 = f (a2) = f (f (a))), . . ., an+1 = f (an), where f is a continuous function. If lim n→∞an = L, show that f (L) = L. (b). Illustrate part (a) by taking f (x) = cos x, a = 1, and estimating the value of L to five decimal p
> Show that the sequence defined by satisfies 0 1 а, — 2 an+1 %3D 3 — а.
> Find a formula for the general term an of the sequence, assuming that the pattern of the first few terms continues. {1,. }, 4. . ...} {* 1 1 1 1. 3.3,7, 9,
> Find the limit of the sequence {√2, √2√2, √2√2√2, …}
> If you deposit $100 at the end of every month into an account that pays 3% interest per year compounded monthly, the amount of interest accumulated after months is given by the sequence (a). Find the first six terms of the sequence. (b). How much inter
> If $1000 is invested at 6% interest, compounded annually, then after years the investment is worth an = 1000 (1.06)n dollars. (a). Find the first five terms of the sequence {an}. (b). Is the sequence convergent or divergent? Explain.
> Show that the series is convergent. How many terms of the series do we need to add in order to find the sum to the indicated accuracy? (-1)" Σ R-1 n 5* (lerror|< 0.0001)
> Use a graph of the sequence to decide whether the sequence is convergent or divergent. If the sequence is convergent, guess the value of the limit from the graph and then prove your guess. 1.3. 5.. an - (2n – 1) (2n)"
> List the first nine terms of the sequence {cos(nπ/3)}. Does this sequence appear to have a limit? If so, find it. If not, explain why.
> Use a graph of the sequence to decide whether the sequence is convergent or divergent. If the sequence is convergent, guess the value of the limit from the graph and then prove your guess. n' cos n a, 1+ n? 2
> Use a graph of the sequence to decide whether the sequence is convergent or divergent. If the sequence is convergent, guess the value of the limit from the graph and then prove your guess. 34 + 5a
> Use a graph of the sequence to decide whether the sequence is convergent or divergent. If the sequence is convergent, guess the value of the limit from the graph and then prove your guess. 3 + 2n? V 8n? + n =
> Use a graph of the sequence to decide whether the sequence is convergent or divergent. If the sequence is convergent, guess the value of the limit from the graph and then prove your guess. a, = /n sin(7//n)
> Determine whether the sequence converges or diverges. If it converges, find the limit. (-3)" n!
> Determine whether the sequence converges or diverges. If it converges, find the limit. а, — In(2n? + 1) — In(n? + 1)
> Determine whether the sequence converges or diverges. If it converges, find the limit. (In n)? de
> Determine whether the sequence converges or diverges. If it converges, find the limit. {0, 1, 0, 0, 1, 0, 0, 0, 1, ...}
> Find the radius of convergence and interval of convergence of the series. 00 (х — 2)" 2 A-0 n + 1
> Determine whether the sequence converges or diverges. If it converges, find the limit. (2л — 1)! in (2n + 1)!
> Determine whether the sequence converges or diverges. If it converges, find the limit. 1+3a
> Determine whether the sequence converges or diverges. If it converges, find the limit. an 1 +
> Determine whether the sequence converges or diverges. If it converges, find the limit. {n cos nT}
> Determine whether the sequence converges or diverges. If it converges, find the limit. cos'n 2"
> Determine whether the sequence converges or diverges. If it converges, find the limit. {arctan 2n}
> Determine whether the sequence converges or diverges. If it converges, find the limit. {n°e"}
> Determine whether the sequence converges or diverges. If it converges, find the limit. a, = cos(2/n)
> Determine whether the sequence converges or diverges. If it converges, find the limit. [e^ + e-^] - 1 2n e
> (a). What is a convergent sequence? Give two examples. (b). What is a divergent sequence? Give two examples.
> Find the radius of convergence and interval of convergence of the series. (2n)! Σ 00 2"
> Determine whether the sequence converges or diverges. If it converges, find the limit. (-1)*-'n n? + 1
> Determine whether the sequence converges or diverges. If it converges, find the limit. 2nt tan 1+ 8n
> Determine whether the sequence converges or diverges. If it converges, find the limit. 3a+2 a. 5"
> Determine whether the sequence converges or diverges. If it converges, find the limit. a, = el/a
> Determine whether the sequence converges or diverges. If it converges, find the limit. п+ 1
> In the figure there are infinitely many circles approaching the vertices of an equilateral triangle, each circle touching other circles and sides of the triangle. If the triangle has sides of length 1, find the total area occupied by the circles.
> Consider the series∑∞n-1n/ (n + 1)!. (a). Find the partial sums s1, s2, s3 and s4. Do you recognize the denominators? Use the pattern to guess a formula for sn. (b). Use mathematical induction to prove your guess. (c). Show that the given infinite series
> (a). A sequence {an} is defined recursively by the equation an = ½ (an-1 + an-2) for n > 3, where a1 and a2 can be any real numbers. Experiment with various values of a1 and a2 and use your calculator to guess the limit of the sequence. (b). Find limn→∞
> The Cantor set, named after the German mathematician Georg Cantor (1845–1918), is constructed as follows. We start with the closed interval [0, 1] and remove the open interval (1/3, 2/3). That leaves the two intervals [0, 1/3] and [2/3,
> (a). What is a sequence? (b). What does it mean to say that limn→∞ an = 8? (c). What does it mean to say that limn→∞ an = ∞?
> The Fibonacci sequence was defined in Section 8.1 by the equations Show that each of the following statements is true. fi = 1, fi= 1, fa= fa-1 + fa-2 %3D n> 3 1 (a) fa-1 fa+1 fa-1 fa fafa+1 1 1 1 = 1 -2 fa-1 fa+1 (b) E fa (c) E = 2 a-2 fa-1 fa+1
> Suppose that a series ∑ an has positive terms and its partial sums Sn satisfy the inequality Sn < 100 for all n. Explain why ∑an must be convergent.
> If ∑ an and ∑bn are both divergent, is ∑ (an + bn) necessarily divergent?
> If ∑ an is convergent and ∑bn is divergent, show that the series ∑(an + bn) is divergent. [Hint: Argue by contradiction.]
> A sequence is defined recursively by Find the first eight terms of the sequence {an}. What do you notice about the odd terms and the even terms? By considering the odd and even terms separately, show that {an} is convergent and deduce that This give
> The size of an undisturbed fish population has been modeled by the formula where Pn is the fish population after n years and a and b are positive constants that depend on the species and its environment. Suppose that the population in year 0 is p0 >
> A right triangle ABC is given with ∠A = θ and |AC| = b. CD is drawn perpendicular to AB, DE, is drawn perpendicular to BC, EF ⊥ AB, and this process is continued indefinitely, as shown in the figure. Find t
> The figure shows two circles C and D of radius 1 that touch at P. Tis a common tangent line; C1 is the circle that touches C, D, and T; C2 is the circle that touches C, D, and C1; C3 is the circle that touches C, D, and C2. This procedure can be continue
> Graph the curves y = xn, 0 00 Σ Ei n(n + 1) = 1
> Show that the sequence defined by is increasing and an a, = 1 az+1 = 3 - an
> Find at least 10 partial sums of the series. Graph both the sequence of terms and the sequence of partial sums on the same screen. Does it appear that the series is convergent or divergent? If it is convergent, find the sum. If it is divergent, explain w
> A sequence {an} is given by a1 = √2, an+1 = √2 + an. (a). By induction or otherwise, show that is increasing and bounded above by 3. Apply the Monotonic Sequence Theorem to show that lim n→∞ an exists. (b). Find limn lim n→∞ an.
> Suppose you know that {an} is a decreasing sequence and all its terms lie between the numbers 5 and 8. Explain why the sequence has a limit. What can you say about the value of the limit?
> A certain ball has the property that each time it falls from a height h onto a hard, level surface, it rebounds to a height rh, where 0 < r < h. Suppose that the ball is dropped from an initial height H of meters. (a). Assuming that the ball continues to
> When money is spent on goods and services, those who receive the money also spend some of it. The people receiving some of the twice-spent money will spend some of that, and so on. Economists call this chain reaction the multiplier effect. In a hypotheti
> Find the radius of convergence and interval of convergence of the series. (-1)ª-'x" Σ 00 3
> Find the radius of convergence and interval of convergence of the series. (-1)"x" 00 -о п + 1 A-0
> Find the radius of convergence and interval of convergence of the series. x" Σ 00
> (a). What is the radius of convergence of a power series? How do you find it? (b). What is the interval of convergence of a power series? How do you find it?
> To control an agricultural pest called the medfly (Mediterranean fruit fly), N sterilized male flies are released into the general fly population every day. If is the proportion of these sterilized flies that survive a given day, then Nsk will survive fo
> What is a power series?
> Explain how Euler’s method works.
> (a). Use Euler’s method with step size 0.2 to estimate y (0.4), where y (x) is the solution of the initial-value problem (b). Repeat part (a) with step size 0.1. (c). Find the exact solution of the differential equation and compare th
> What can you say about the solutions of the equation y' = x2 + y2 just by looking at the differential equation?
> A bacteria culture contains 200 cells initially and grows at a rate proportional to its size. After half an hour the population has increased to 360 cells. (a). Find the number of bacteria after hours. (b). Find the number of bacteria after 4 hours. (c).
> The Brentano-Stevens Law in psychology models the way that a subject reacts to a stimulus. It states that if R represents the reaction to an amount of stimulus, then the relative rates of increase are proportional: where is a positive constant. Find R as
> The von Bertalanffy growth model is used to predict the length L (t) of a fish over a period of time. If L∞ is the largest length for a species, then the hypothesis is that the rate of growth in length is proportional to L∞ - L, the length yet to be achi
> (a). Write a differential equation that expresses the law of natural growth. What does it say in terms of relative growth rate? (b). Under what circumstances is this an appropriate model for population growth? (c). What are the solutions of this equation
> (a). Write the solution of the initial-value problem and use it to find the population when t = 20. (b). When does the population reach 1200? dP P 0.1P(1 P(0) 100 dt 2000
> A cup of hot chocolate has temperature 800Cin a room kept at 200C. After half an hour the hot-chocolate cools to 600C. (a). What is the temperature of the chocolate after another half hour? (b). When will the chocolate have cooled to 400C?
> A patient is prescribed a drug and is told to take one 100-mg pill every eight hours. After eight hours, about 5% of the drug remains in the body. (a). What quantity of the drug remains in the body after the patient takes three pills? (b). What quantity
> Let C (t) be the concentration of a drug in the bloodstream. As the body eliminates the drug, C (t) decreases at a rate that is proportional to the amount of the drug that is present at the time. Thus C (t) = -kC (t), where is a positive number called th
> Cobalt-60 has a half-life of 5.24 years. (a). Find the mass that remains from a 100-mg sample after 20 years. (b). How long would it take for the mass to decay to 1 mg?
> A planning engineer for a new alum plant must present some estimates to his company regarding the capacity of a silo designed to contain bauxite ore until it is processed into alum. The ore resembles pink talcum powder and is poured from a conveyor at th
> Find the orthogonal trajectories of the family of curves. y = e kx
> Find the orthogonal trajectories of the family of curves. y = kex
> Solve the initial-value problem. (1 + cos x)y' = (1 + e-y) sin x, y (0) = 0
> Solve the initial-value problem. dr/dt + 2tr = r, r (0) = 5
> Solve the differential equation. dx/dt = 1 – t + x - rx
> Find the curve y = f (x) such that f (x) > 0, f (0) = 0, f (1) = 1, and the area under the graph of f from 0 to x is proportional to the (n + 1) power of f (x).
> Find all functions f that satisfy the equation (f (x)dx) (f 1/f (x) dx) = -1
> (a). If lima→∞ an = L, what is the value of lima→∞ an+1? (b). A sequence {an} is defined by Find the first ten terms of the sequence correct to five decimal places. Does it appear

