Question: Determine whether the series is convergent or
Determine whether the series is convergent or divergent by expressing Sn as a telescoping sum (as in Ex am ple 6). If it is convergent, find its sum.
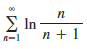
Transcribed Image Text:
00 E In- п+1 A-1
> Find the radius of convergence and interval of convergence of the series. 00 2n Σ a-2 n(In n)?
> Use the sum of the first 10 terms to approximate the sum of the series. Estimate the error. 1 Σ Vn' + 1 00
> How many terms of the series ∑∞n=1 1/ [n (ln n)2] would you need to add to find its sum to within 0.01?
> Estimate ∑∞n=1 (2n + 1)-6 correct to five decimal places.
> Find the sum of the series ∑∞n=1 1/n5 correct to three decimal places.
> (a). Use the sum of the first 10 terms to estimate the sum of the series∑∞n=1 1/n2. How good is this estimate? (b). Improve this estimate using (4) with n = 10. (c). Find a value of that will ensure that the error in the approximation s ≈ sn is less than
> (a). Find the partial sum s10 of the series∑∞n-1 1/n4. Estimate the error in using s10 as an approximation to the sum of the series. (b). Use (4) with n = 10 to give an improved estimate of the sum. (c). Find a value of n so that sn is within 0.00001 of
> Find the values of p for which the following series is convergent. 1 Σ -2 n(ln n)P 00
> Determine whether the series is convergent or divergent. ∑∞n=1 n2 – 5n/n3 + n + 1
> List the first six terms of the sequence defined by an = n/2n + 1 Does the sequence appear to have a limit? If so, find it.
> Determine whether the series is convergent or divergent. ∑∞n=1 sin (1/n)
> Find the radius of convergence and interval of convergence of the series. n (x – a)", b>0
> Determine whether the series is convergent or divergent. ∑∞n=0 1 + sin n/10n
> Determine whether the series is convergent or divergent. ∑∞n=1 2 + (-1)n n √n
> Determine whether the series is convergent or divergent. If it is convergent, find its sum. Σ (cos 1 ) k-1
> Determine whether the series is convergent or divergent. ∑∞n=1 1 + 4n/1 + 3n
> Determine whether the series is convergent or divergent. 1/5 + 1/8 + 1/11 + 1/14 + 1/17+ …
> Determine whether the series is convergent or divergent. 1 + 1/3 + 1/5 + 1/7 + 1/9 + …
> Determine whether the series is convergent or divergent. ∑∞n=1 4 + 3n/2n
> Determine whether the series is convergent or divergent. ∑∞n=1 n – 1/n4n
> Determine whether the series is convergent or divergent. ∑∞n=1 n2 – 1/3n4 + 1
> Determine whether the series is convergent or divergent. ∑∞n=1 cos2n/n2 + 1
> Determine whether the sequence converges or diverges. If it converges, find the limit. (-1)*n n + 2n² + 1
> Determine whether the series is convergent or divergent. ∑∞n=1 1/n2 + 9
> Determine whether the series is convergent or divergent. ∑∞n=2 1/n ln n
> Determine whether the series is convergent or divergent. 1 + 1/8 + 1/27 + 1/64 + 1/125 + . . .
> Determine whether the series is convergent or divergent. ∑∞n=1 (n-14 + 3n-12)
> Determine whether the series is convergent or divergent. ∑∞n=1 2/n0.85
> Use the Comparison Test to determine whether the series is convergent or divergent. 00 .3 Σ n² – 1
> Let an = 2n/3n + 1 (a). Determine whether {an} is convergent. (b). Determine whether ∑∞n-1 an is convergent.
> Find at least 10 partial sums of the series. Graph both the sequence of terms and the sequence of partial sums on the same screen. Does it appear that the series is convergent or divergent? If it is convergent, find the sum. If it is divergent, explain w
> Find at least 10 partial sums of the series. Graph both the sequence of terms and the sequence of partial sums on the same screen. Does it appear that the series is convergent or divergent? If it is convergent, find the sum. If it is divergent, explain w
> Find at least 10 partial sums of the series. Graph both the sequence of terms and the sequence of partial sums on the same screen. Does it appear that the series is convergent or divergent? If it is convergent, find the sum. If it is divergent, explain w
> Find the radius of convergence and interval of convergence of the series. E n!(2x 1)"
> Find at least 10 partial sums of the series. Graph both the sequence of terms and the sequence of partial sums on the same screen. Does it appear that the series is convergent or divergent? If it is convergent, find the sum. If it is divergent, explain w
> Find a formula for the general term an of the sequence, assuming that the pattern of the first few terms continues. {5, 1, 5, 1, 5, 1, . ..}
> (a). Determine whether the sequence defined as follows is convergent or divergent: (b). What happens if the first term is a1 = 2? a, = 1 an+1 = 4 - a, for n>1
> We have seen that the harmonic series is a divergent series whose terms approach 0. Show that is another series with this property. 00 2 In( 1 + A-1
> Find the values of x for which the series converges. Find the sum of the series for those values of x. 00 cos"x Σ 24 n-0
> Find the values of x for which the series converges. Find the sum of the series for those values of x. (х + 3)" Σ 24 A-0
> Find the values of x for which the series converges. Find the sum of the series for those values of x. 3" n-
> Express the number as a ratio of integers. 7. ¯12345
> Find at least 10 partial sums of the series. Graph both the sequence of terms and the sequence of partial sums on the same screen. Does it appear that the series is convergent or divergent? If it is convergent, find the sum. If it is divergent, explain w
> Express the number as a ratio of integers. 1. ¯5342
> Find the radius of convergence and interval of convergence of the series. - 4)ª n(x – 4)" n + 1 A-1
> Express the number as a ratio of integers. 6. ¯254 = 6.2545454…
> Express the number as a ratio of integers. 0. ¯2 = 0.2222…
> Express the number as a ratio of integers. 0. ¯73 = 0.73737373…
> Use a graph of the sequence to decide whether the sequence is convergent or divergent. If the sequence is convergent, guess the value of the limit from the graph and then prove your guess. a, = 1 + (-2/e)"
> Determine whether the series is convergent or divergent by expressing Sn as a telescoping sum (as in Ex am ple 6). If it is convergent, find its sum. 3 Σ п(n + 3) A-1
> Determine whether the series is convergent or divergent by expressing Sn as a telescoping sum (as in Ex am ple 6). If it is convergent, find its sum. 00 2 Σ A-1 n + 4n + 3
> Determine whether the series is convergent or divergent by expressing Sn as a telescoping sum (as in Ex am ple 6). If it is convergent, find its sum. 2 Σ n² – 1 ,2
> Determine whether the sequence converges or diverges. If it converges, find the limit. sin 2n 1 + + Jn
> Determine whether the series is convergent or divergent. If it is convergent, find its sum. 1 Σ п(n + 1) A-1 +
> Find the radius of convergence and interval of convergence of the series. (4x + 1)" n? 00 n-1
> Determine whether the series is convergent or divergent. If it is convergent, find its sum. E [(0.8)*-1 – (0.3)*]
> Determine whether the series is convergent or divergent. If it is convergent, find its sum. Σ 2 arctan n
> Determine whether the series is convergent or divergent. If it is convergent, find its sum. -1
> Determine whether the series is convergent or divergent. If it is convergent, find its sum. 1+ 3" 24
> Determine whether the series is convergent or divergent. If it is convergent, find its sum. 1+ 24 Σ 34
> Determine whether the series is convergent or divergent. If it is convergent, find its sum. 00 Σ cos A-1
> Determine whether the series is convergent or divergent. If it is convergent, find its sum. k? Σ k? – 1 00 - 1 k-2
> Determine whether the series is convergent or divergent. If it is convergent, find its sum. k(k + 2) Σ -i (k + 3)2 k-1
> Explain what it means to say that ∑∞n-1 an = 5.
> Determine whether the series is convergent or divergent. If it is convergent, find its sum. n - 1 Σ A-1 3n Зп — 1
> Show that the series is convergent. How many terms of the series do we need to add in order to find the sum to the indicated accuracy? E (-1)*-'ne- (1 error|< 0.01)
> Determine whether the geometric series is convergent or divergent. If it is convergent, find its sum. Σ n-0
> Determine whether the geometric series is convergent or divergent. If it is convergent, find its sum. 00 Σ A-o 3*+1
> Determine whether the geometric series is convergent or divergent. If it is convergent, find its sum. 10" Σ (-9)*-1
> Determine whether the geometric series is convergent or divergent. If it is convergent, find its sum. 00 E 6(0.9)“-! A-1 n-1
> Determine whether the geometric series is convergent or divergent. If it is convergent, find its sum. 1 + 0.4 + 0.16 + 0.064 +
> Determine whether the geometric series is convergent or divergent. If it is convergent, find its sum. 10 – 2 + 0.4 – 0.08 + ·
> Determine whether the geometric series is convergent or divergent. If it is convergent, find its sum. 4 + 3 ++ + ...
> Determine whether the geometric series is convergent or divergent. If it is convergent, find its sum. 3 – 4 +4 - + ... 16
> (a). Explain the difference between (b). Explain the difference between aj and 内I and E aj
> (a). What is the difference between a sequence and a series? (b). What is a convergent series? What is a divergent series?
> Show that the series is convergent. How many terms of the series do we need to add in order to find the sum to the indicated accuracy? (-1)*+1 (lerror|< 0.00005) A-1
> (a). What is an alternating series? (b). Under what conditions does an alternating series converge? (c). If these conditions are satisfied, what can you say about the remainder after n terms?
> On what interval is the curve y = fx0 t2/t2 + t + 2, dt concave downward?
> If f (x) = fsinxo√1 + t2 dt and g (y) = fy3 f(x) dx, find g"(π/6).
> If f (x) = fx0 (1 – t2) et2 dt, on what interval is f increasing?
> Evaluate the integral. f01 10x dx
> Evaluate the integral. f12 x-2 dx
> Evaluate the integral. f1/2√3/2 6/√1 – t2 dt
> find f. f'(x) = √x (6 + 5x) f (1) = 10
> find f. f'(x) = 8x3 + 12x + 3, f (1) = 6
> Find f. f"(x) = 1 - 6x, f (0) = 8
> Find f. f"(x) = 6x + sin x
> Find f. f"(x) = 6x + 12x2
> Use Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function. *cos X y = * (1 + v?)1º dv Jsin x
> Find the antiderivative F of f that satisfies the given condition. Check your answer by comparing the graphs of f and F. f(x) — 4 — 3(1 + х?)-1, F(1) = 0
> Find the antiderivative F of f that satisfies the given condition. Check your answer by comparing the graphs of f and F. f(x) = 5x* – 2x', F(0)=4
> Find the most general antiderivative of the function. (Check your answer by differentiation.) f(x) = 27 + 6 cos x COS %3D
> Find the most general antiderivative of the function. (Check your answer by differentiation.) g(8) = cos e – 5 sin e
> Find the most general antiderivative of the function. (Check your answer by differentiation.) f(x) = 3e* + 7 sec?x
> Let S be the solid obtained by rotating the region shown in the figure about the y-axis. Sketch a typical cylindrical shell and find its circumference and height. Use shells to find the volume of S. Do you think this method is preferable to slicing? Expl
> Evaluate the limit by first recognizing the sum as a Riemann sum for a function defined on [0, 1]. 2 3 lim +
> Evaluate the limit by first recognizing the sum as a Riemann sum for a function defined on [0, 1]. lim 4
> The area labeled B is three times the area labeled A. Express a in terms of b. y. y= e" y= e" B A a
> Suppose h is a function such that h (1) = -2, h'(1) = 2, h"(1) = 3, h (2) = 6, h'(2) = 5, h"(2) = 13, and h" is continuous everywhere. Evaluate f21 h"(u) du.

