Question: Determine whether the statement is true or
Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement.
1. If f is a function, then f (s + t) = f (s) + f (t).
2. If f (s) = f (t), then s = t.
3. If f is a function, then f (3x) = 3f (x).
4. If x1 f (x2).
5. A vertical line intersects the graph of a function at most once.
6. If f and g are functions, then f0g = g0f.
7. If f is one-to-one, then f-1 (x) = 1/f (x).
8. You can always divide by ex.
9.If 0 10. If x > 0, then (ln x)6 ln x.
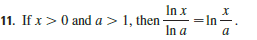
12. The parametric equations x = t2, y = t4 have the same graph as x = t3, y = t6.
Transcribed Image Text:
In x 11. If x > 0 and a> 1, then In a a
> Using periodic trends, rank Br, I, and F in order of increasing a. atomic size b. ionization energy c. electron affinity
> The pair of reactions catalyzed by aconitase results in the conversion of isocitrate to its isomer citrate. What are isomers?
> Discuss the difference between theory and scientific law.
> What is the function of colipase in the digestion of dietary lipids?
> Describe the process occurring at the molecular level that accounts for the property of surface tension.
> The model of methane in Question 1.27 has limitations, as do all models. What are these limitations? Question 1.27: What are the characteristics of methane emphasized by the following model? H H°c H H
> a. What are very low-density lipoproteins? b. Compare the function of VLDLs with that of chylomicrons.
> What data would be required to estimate the mass of planet earth?
> Why are triglycerides more efficient energy-storage molecules than glycogen?
> Why is observation a critical starting point for any scientific study?
> Why are the lipases that are found in saliva and in the stomach not very effective at digesting triglycerides?
> Define energy and explain the importance of energy in chemistry.
> What is the major metabolic function of adipose tissue?
> Convert 2.00 × 102 J to units of cal.
> What tissue is the major storage depot for lipids?
> How does the reaction described in Question 22.101 allow the citric acid cycle to fulfill its roles in both catabolism and anabolism? Question 22.101: Write a balanced equation for the reaction catalyzed by pyruvate carboxylase.
> Report the result of each of the following operations using the proper number of significant figures: 27.2 x 15.63 а. 4.79 x 105 с. 3.58 е. 4.0 1.84 0.7911 11.4 x 10-4 f. 13.6 b. 18.02 x 1.6 d. 3.58 x 4.0 = 0.45
> Why is colipase needed for lipid digestion?
> Report the result of the following addition to the proper number of significant figures and in scientific notation. 4.80 × 108 + 9.149 × 102
> Draw the structure of a triglyceride composed of glycerol, palmitoleic acid, linolenic acid, and oleic acid.
> Report the result of each of the following to the proper number of significant figures: a. 7.939 + 6.26 = b. 2.4 - 8.321 = c. 2.333 + 1.56 - 0.29 =
> In Figure 23.1, a micelle composed of the phospholipid lecithin is shown. Why is lecithin a good molecule for the formation of micelles? Figure 23.1: H,C-0-C-R,. HC-0-C-R2 НС — О— Р-О -0 CH2 CH2 CH, +N4 -CH3 CH3
> Using the periodic table, write the symbol for each of the following and label as a metal, metalloid, or nonmetal. a. sulfur b. oxygen c. phosphorus d. nitrogen
> To what class of lipids do the bile salts belong?
> Represent each of the following numbers in scientific notation, showing only significant digits: a. 48.20 b. 480.0 c. 0.126 d. 9,200 e. 0.0520 f. 822
> Summarize the effects of the hormone glucagon on carbohydrate and lipid metabolism.
> Draw the Lewis structure of each of the following compounds and predict its geometry using the VSEPR theory. a. SeO2 b. SeO3
> Predict which of the following bonds are polar, and, if polar, use a vector to indicate in which direction the electrons are pulled: a. Si—Cl b. S—Cl c. H—C d. C—C
> List five biological activities that require ATP.
> Use transformations to sketch the graph of the function. y = -sin 2x
> Draw, by hand, a rough sketch of the graph of each function. (a). y = sin x (b). y = tan x (c). y = ex (d). y = ln x (e). y = 1/x (f). y = |x| (g). y = √x
> Sketch by hand, on the same axes, the graphs of the following functions. (a). f (x) = x (b). g (x) = x2 (c). h (x) = x3 (d). j (x) = x4
> What is a mathematical model?
> What is an increasing function?
> How is the composite function f0g defined? What is its domain?
> (a). Sketch the curve by using the parametric equations to plot points. Indicate with an arrow the direction in which the curve is traced as t increases. (b). Eliminate the parameter to find a Cartesian equation of the curve. х 3 3t — 5, у 3D 2t + 1
> Sketch the curve by using the parametric equations to plot points. Indicate with an arrow the direction in which the curve is traced as increases. x = t? + 1, y = t² - t, -2 <t< 2
> A function is given by a table of values, a graph, a formula, or a verbal description. Determine whether it is one-to-one. f (x) = x2 - 2x
> A function is given by a table of values, a graph, a formula, or a verbal description. Determine whether it is one-to-one. y
> (a). What is a parametric curve? (b). How do you sketch a parametric curve? (c). Why might a parametric curve be more useful than a curve of the form y = f (x)?
> A function is given by a table of values, a graph, a formula, or a verbal description. Determine whether it is one-to-one.
> A function is given by a table of values, a graph, a formula, or a verbal description. Determine whether it is one-to-one. у.
> A function is given by a table of values, a graph, a formula, or a verbal description. Determine whether it is one-to-one. yA
> A function is given by a table of values, a graph, a formula, or a verbal description. Determine whether it is one-to-one. 1 2 3 4 5 6 f(x) 1.0 1.9 2.8 3.5 3.1 2.9
> Find the exact value of each expression. (a). log2 6 - log2 15 + log2 20 (b). log3 100 - log3 18 - log3 50
> Let g (x) = 3√1-x3. (a). Find g-1. How is it related to g? (b). Graph g. How do you explain your answer to part (a)?
> A function is given by a table of values, a graph, a formula, or a verbal description. Determine whether it is one-to-one. 1 2 3 4 5 6 f(x) 1.5 2.0 3.6 5.3 2.8 2.0
> Find an explicit formula for f-1 and use it to graph f-1, f and the line y = x on the same screen. To check your work, see whether the graphs of f and f-1 are reflections about the line. f(x) = x* + 1, I> 0
> Find a formula for the inverse of the function. f (x) = 1 + √2 + 3x
> (a). Eliminate the parameter to find a Cartesian equation of the curve. (b). Sketch the curve and indicate with an arrow the direction in which the curve is traced as the parameter increases. x = tan*e, y = sec 0, -7/2 < 0 < m/2
> (a). If f0 (x) = 1/ 2-x and fn+1 = f00 fn for n = 0, 1, 2, find an expression for fn (x) and use mathematical induction to prove it. (b). Graph f0, f1, f2, f3 on the same screen and describe the effects of repeated composition.
> Prove that 1 + 3 + 5 + … + (2n -1) = n2.
> Prove that if n is a positive integer, then 7n -1 is divisible by 6.
> Is it true that f 0 (g+ h) = f0g + f0h?
> A driver sets out on a journey. For the first half of the distance she drives at the leisurely pace of 30 mi/h; she drives the second half at 60 mi/h. What is her average speed on this trip?
> Use indirect reasoning to prove that log25 is an irrational number.
> Sketch the region in the plane consisting of all points (x, y) such that |x – y| + |x| - |y| < 2
> Sketch the region in the plane consisting of all points (x, y) such that |x| + |y| < 1.
> Draw the graph of the equation x + |x| = y + |y|.
> Solve the inequality |x – 1| - |x - 3| > 5.
> Suppose the graph of f is given. Write an equation for each of the graphs that are obtained from the graph of f as follows. (a). Shift 2 units upward. (b). Shift 2 units downward. (c). Shift 2 units to the right. (d). Shift 2 units to the left. (e). Refl
> Solve the equation |2x – 1| - |x – 5| = 3.
> (a). Find parametric equations for the set of all points P determined as shown in the figure such that |OP| = |AB|. (This curve is called the cissoid of Diocles after the Greek scholar Diocles, who introduced the cissoid as a graphical method for constru
> (a). Find parametric equations for the path of a particle that moves counterclockwise halfway around the circle (x – 2)2 + y2 = 4, from the top to the bottom. (b). Use the equations from part (a) to graph the semicircular path.
> Graph members of the family of functions f (x) = ln (x2 -c) for several values of c. How does the graph change when changes?
> A small-appliance manufacturer finds that it costs $9000 to produce 1000 toaster ovens a week and $12,000 to produce 1500 toaster ovens a week. (a). Express the cost as a function of the number of toaster ovens produced, assuming that it is linear. Then
> Life expectancy improved dramatically in the 20th century. The table gives the life expectancy at birth (in years) of males born in the United States. Use a scatter plot to choose an appropriate type of model. Use your model to predict the life span of a
> Find an expression for the function whose graph consists of the line segment from the point (-2, 2) to the point (-1, 0) together with the top half of the circle with center the origin and radius 1.
> Determine whether is even, odd, or neither even nor odd. (a). f (x) = 2x5 – 3x2 + 2 (b). f (x) = x3 – x7 (c). f (x) = e-x2 (d). f (x) = 1 + sin x
> The graph of f is given. Draw the graphs of the following functions. 1 (а) у — /(x — 8) (c) у — 2 — f(u) (e) y =f-(x) (b) у — —f(x) (d) у — /) — 1 (f) y = f-(x + 3)
> Suppose that the graph of f is given. Describe how the graphs of the following functions can be obtained from the graph of f. (а) у — f() + 8 (с) у — 1 + 2f(х) (е) у — —f(») (b) у —f(x + 8) (d) у — f(x — 2) — 2 (f) y =f-(x)
> (a). What is an even function? How can you tell if a function is even by looking at its graph? (b). What is an odd function? How can you tell if a function is odd by looking at its graph?
> The graph of is given. (a). State the value of g (2). (b). Why is one-to-one? (c). Estimate the value of g-1 (2). (d). Estimate the domain of g-1. (e). Sketch the graph of g-1. 0 1
> (a). If we shift a curve to the left, what happens to its reflection about the line y = x? In view of this geometric principle, find an expression for the inverse of g (x) = f (x + c), where f is a one-to-one function. (b). Find an expression for the inv
> Starting with the graph of y = ln x, find the equation of the graph that results from (a). shifting 3 units upward (b). shifting 3 units to the left (c). reflecting about the x-axis (d). reflecting about the y-axis (e). reflecting about the line y = x (f
> Let f be the function whose graph is given. f (a). Estimate the value of f (2). (b). Estimate the values of such that f (x) = 3. (c). State the domain of f. (d). State the range of f. (e). On what interval is f increasing? (f). Is f one-to-one? Explain
> (a). What is a one-to-one function? How can you tell if a function is one-to-one by looking at its graph? (b). If f is a one-to-one function, how is its inverse function defined? How do you obtain the graph of f-1 from the graph of f?
> (a). If g (x) = x6 + x4, x > 0 use a computer algebra system to find an expression for g-1 (x). (b). Use the expression in part (a) to graph y = g (x), y = x, and y = g-1 (x) on the same screen.
> Graph the function f (x) = √x3 + x2 + x + 1 and explain why it is one-to-one. Then use a computer algebra system to find an explicit expression for f-1(x). (Your CAS will produce three possible expressions. Explain why two of them are irrelevant in this
> Suppose that f has domain A and g has domain B. (a). What is the domain of f + g? (b). What is the domain of fg? (c). What is the domain of f/g?
> Starting with the graph of y = ex, find the equation of the graph that results from (a) reflecting about the line y = 4 (b) reflecting about the line x = 2
> Compare the functions f (x) = x0.1 and g (x) = in x by graphing both f and g in several viewing rectangles. When does the graph of f finally surpass the graph of g?
> Graph the given functions on a common screen. How are these graphs related? у 3 3, у— 10+, у-()', у— (Э)"
> Use Formula 10 to graph the given functions on a common screen. How are these graphs related? y = ln x, y = log10 x, y = ex, y = 10x
> Use Formula 10 to graph the given functions on a common screen. How are these graphs related? y = log1.5 x, y = ln x, y = log10 x, y = log50 x
> Graph several members of the family of functions f (x) = 1 /1 + aebx where a > 0. How does the graph change when changes? How does it change when a change?
> Let f(x) = √1-x2, o < x < 1 (a). Find f-1. How is it related to f? (b). Identify the graph of f and explain your answer to part (a).
> A bacterial culture starts with 500 bacteria and doubles in size every half hour. (a). How many bacteria are there after 3 hours? (b). How many bacteria are there after t hours? (c). How many bacteria are there after 40 minutes? (d). Graph the population
> Make a rough sketch of the graph of each function. Do not use a calculator. Just use the graphs given in Figures 12 and 13 and, if necessary, the transformations of Section 1.3. Figures 12: Figures 13: (a). y = ln (-x) (b). y = ln |x| y y= log,
> Make a rough sketch of the graph of each function. Do not use a calculator. Just use the graphs given in Figures 12 and 13 and, if necessary, the transformations of Section 1.3. Figures 12: Figures 13: (a). y = log10(x + 5) (b). y = -ln x y y=
> Investigate the family of curves defined by the parametric equations x = cos t, y = sin t – sin ct, where c > 0. Start by letting be a positive integer and see what happens to the shape as c increases. Then explore some of the possibilities that occur wh
> The curves with equations x = a sin nt, y = b cos t is called Lissajous figures. Investigate how these curves vary when a, b, and n vary. (Take n to be a positive integer.)
> The swallowtail catastrophe curves are defined by the parametric equations x = 2ct - 4t3, y = -ct2 + 3t4. Graph several of these curves. What features do the curves have in common? How do they change when c increases?
> Graph the given functions on a common screen. How are these graphs related? у %3е*, у—е", у38%, у- 8*
> Investigate the family of curves defined by the parametric equations x = t2, y = t3 - ct. How does the shape change c as increases? Illustrate by graphing several members of the family.
> If a projectile is fired with an initial velocity of meters per second at an angle a above the horizontal and air resistance is assumed to be negligible, then its position after seconds is given by the parametric equations where is the acceleration due
> Suppose that the position of one particle at time is given by x1 = 3 sin t y1 = 2 cos t 0 (a). Graph the paths of both particles. How many points of intersection are there? (b). Are any of these points of intersection collision points? In other words,
> A curve, called a witch of Maria Agnesi, consists of all possible positions of the point P in the figure. Show that parametric equations for this curve can be written as Sketch the curve. x = 2a cot e y = 2a sin?e y у. C y = 2a --- at
> If and are fixed numbers, find parametric equations for the curve that consists of all possible positions of the point P in the figure, using the angle θ as the parameter. Then eliminate the parameter and identify the curve. \b
> Let P be a point at a distance d from the center of a circle of radius r. The curve traced out by P as the circle rolls along a straight line is called a trochoid. (Think of the motion of a point on a spoke of a bicycle wheel.) The cycloid is the special

