Question: Disk drives have been getting larger. Their
Disk drives have been getting larger. Their capacity is now often given in terabytes (TB) where 1 TB = 1000 gigabytes, or about a trillion bytes. A search of prices for external disk drives on Amazon.com in mid-2016 found the following data: (Data in Disk drives 2016)
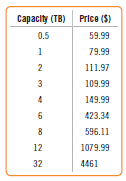
1. Consider the following data from a small bookstore.
a) Prepare a scatterplot of Price against Capacity.
b) What can you say about the direction of the association?
c) What can you say about the form of the relationship?
d) What can you say about the strength of the relationship?
e) Does the scatterplot show any outliers?
Transcribed Image Text:
Capacity (TB) Price ($) 0.5 59.99 1 79.99 2 111.97 3 109.99 149.99 6 423.34 8 596.11 12 1079.99 32 4461
> A sample of 20 CEOs from the Forbes 500 shows total annual compensations ranging from a minimum of $0.1 to $62.24 million. The average for these 20 CEOs is $7.946 million. The histogram and boxplot are as follows: Based on these data, a computer progr
> A company is interested in estimating the costs of lunch in their cafeteria. After surveying employees, the staff calculated that a 95% confidence interval for the mean amount of money spent for lunch over a period of six months is ($780, $920). Now the
> A feed supply company has developed a special feed supplement to see if it will promote weight gain in livestock. Their researchers report that the 77 cows studied gained an average of 56 pounds and that a 95% confidence interval for the mean weight gain
> Markets have become interested in the potential of social networking sites. But they need to understand the demographics of social networking users. Pew Research has conducted surveys since 2012 that address these questions. (www.pewinternet.org/Reports/
> A market researcher working for the bank in Exercise 2 wants to know if the distribution of applications by card is the same for the past three mailings. She takes a random Inference for Counts: Chi-Square Tests sample of 200 from each mailing and counts
> An analyst at a local bank wonders if the age distribution of customers coming for service at his branch in town is the same as at the branch located near the mall. He selects 100 transactions at random from each branch and researches the age information
> For the data in Exercise 2, a) Compute the standardized residual for each type of card. b) Are any of these particularly large? (Compared to what?) c) What does the answer to part b say about this new group of customers? Exercise 2: At a major credit ca
> For the data in Exercise 1, a) Compute the standardized residual for each season. b) Are any of these particularly large? (Compared to what?) c) Why should you have anticipated the answer to part b? Exercise 1: If there is no seasonal effect on human bi
> A survey designed to study how much households spend on eating out finds the following regression model, relating the amount respondents said they spent individually to eat out each week to their household income in $1000’s. a) A 95%
> For the customers in Exercise 2, a) If the customers apply for the three cards according to the historical proportions, about how big, on average, would you expect the χ2 statistic to be (what is the mean of the χ2 distribution)? b) Does the statistic yo
> For the births in Exercise 1, a) If there is no seasonal effect, about how big, on average, would you expect the x2 statistic to be (what is the mean of the χ2 distribution)? b) Does the statistic you computed in Exercise 1 seem large in comparison to th
> At a major credit card bank, the percentages of people who historically apply for the Silver, Gold, and Platinum cards are 60%, 30%, and 10%, respectively. In a recent sample of customers responding to a promotion, of 200 customers, 110 applied for Silve
> For the data in Exercise 2, a) Test the null hypothesis at a = 0.05 using the pooled t-test. (Show the t-statistic, P-value, and conclusion.) b) Find a 95% confidence interval using the pooled degrees of freedom. c) Are your answers different from wha
> For the data in Exercise 1, a) Test the null hypothesis at a = 0.05 using the pooled t-test. (Show the t-statistic, P-value, and conclusion.) b) Find a 95% confidence interval using the pooled degrees of freedom. c) Are your answers different from wha
> As part of the poll in Exercise 11, Pew asked whether the respondent owned a smartphone. Are Internet use and smartphone ownership independent? a) Under the usual null hypothesis, what are the expected values? b) Compute the χ2 statistic. c)
> A similar Pew poll in 2016 asked people how often they used the Internet. (Data in Income and internet) How often do you use the Internet? a) Under the usual null hypothesis, what are the expected values? b) Compute the χ2 statistic. c) Ho
> From the same survey as in Exercise 9, 294 of the 409 respondents who reported earning less than $30,000 per year said they were social networking users. At the other end of the income scale, 333 of the 504 respondents reporting earnings of $75,000 or mo
> If there is no seasonal effect on human births, we would expect equal numbers of children to be born in each season (winter, spring, summer, and fall). A student takes a census of her statistics class and finds that of the 120 students in the class, 25 w
> Using the data in Exercise 1, and assuming that the data come from a distribution that is Normally distributed, a) Find a 95% confidence interval for the mean difference in ages of houses in the two neighborhoods. b) Is 0 within the confidence interval
> The study of external disk drives from Chapter 4, Exercise 2 (with the outlier removed) finds the following: The least squares line was found to be: a) Find the predicted Price of a 2 TB hard drive. b) Find a 95% confidence interval for the mean Pric
> A website that rents movies online recorded the age and the number of movies rented during the past month for some of their customers. Here are their data: Make a scatterplot for these data. What does it tell you about the relationship between these t
> The histogram of the ages of the respondents in Exercise 22 looks like this: What might you suggest for the next step of the analysis? 15 - 10 40 80 120 160 200 240 Count
> The histogram of the total revenues (in $M) of the movies in Exercise 21 looks like this: What might you suggest for the next step of the analysis? 80 60 40 20 100 200 300 400 500 600 700 800 Gross (SM) Count
> Are the following data time series? If not, explain why. a) Reports from the Bureau of Labor Statistics on the number of U.S. adults who are employed full time in each major sector of the economy. b) The quarterly Gross Domestic Product (GDP) of France f
> Are the following data time series? If not, explain why. a) Quarterly earnings of Microsoft Corp. b) Unemployment in August 2010 by education level. c) Time spent in training by workers in NewCo. d) Numbers of e-mails sent by employees of SynCo each hour
> You wish to explain to your boss what effect taking the base-10 logarithm of the salary values in the company’s database will have on the data. As simple, example values you compare a salary of $10,000 earned by a part-time shipping clerk, a salary of $1
> When analyzing data on the number of employees in small companies in one town, a researcher took square roots of the counts. Some of the resulting values, which are reasonably symmetric were: 4, 4, 6, 7, 7, 8, 10 What were the original values, and how ar
> For the disk drive data of Exercise 2 (as corrected in Exercise 12), find and interpret the value of R2. Exercise 2: Disk drives have been getting larger. Their capacity is now often given in terabytes (TB) where 1 TB = 1000 gigabytes, or about a trilli
> Indicate which of the following represent independent events. Explain briefly. a) Prices of houses on the same block. b) Successive measurements of your heart rate as you exercise on a treadmill. c) Measurements of the heart rates of all students in t
> For the regression model for the bookstore of Exercise 1, what is the value of R2 and what does it mean? Exercise 1: Consider the following data from a small bookstore. Number of Sales People Working Sales (in $1000) 10 3 11 7 13 14 10 18 10 20 12
> Here are residual plots (residuals plotted against predicted values) for three linear regression models. Indicate which condition appears to be violated (linearity, outlier, or equal spread) in each case. a) 15+ 10 5+ -5+ -10+ -10 0 10 20 30 40 50
> Is the experiment of Exercise 1 blind? Could it be made double blind? Explain. Exercise 1: For the following experiment, identify the experimental units, the treatments, the response, and the random assignment. A commercial food lab compared recipes fo
> Here are the residuals for a regression of Sales on Number of Sales People Working for the bookstore of Exercise 1: a) What are the units of the residuals? b) Which residual contributes the most to the sum that was minimized according to the Least Squa
> U.S. Customs and Border Protection has been testing automated kiosks that may be able to detect lies (www .wired.com/threatlevel/2013/01/ff-lie-detector/all/). One measurement used (among several) is involuntary eye movements. Using this method alone, te
> According to U.S. Census data, 68% of the civilian U.S. labor force self-identifies as White, 11% as Black, and the remaining 21% as Hispanic/Latino or Other. Among Whites in the labor force, 54% are Male, and 46% Female. Among Blacks, 52% are Male and 4
> The company in Exercise 13 performed another experiment in which they tested three website designs to see which one would lead to the highest probability of purchase. The first (design A) used enhanced product information, the second (design B) used exte
> Summit Projects provides marketing services and website management for many companies that specialize in outdoor products and services. To understand customer Web behavior, the company experiments with different offers and website design. The results of
> Facebook reports that 70% of their users are from outside the United States and that 50% of their users log on to Facebook every day. Suppose that 20% of their users are United States users who log on every day. a) What percentage of Facebook’s users are
> A national survey indicated that 30% of adults conduct their banking online. It also found that 40% are under the age of 50, and that 25% are under the age of 50 and conduct their banking online. a) What percentage of adults do not conduct their banking
> Using the table from Exercise 8, a) What is the probability that a randomly selected Black multigenerational family is a two-adult-generation family? b) What is the probability that a randomly selected multigenerational family is White, given that it is
> Indicate which of the following represent independent events. Explain brief ly. a) The gender of customers using an ATM machine. b) The last digit of the social security numbers of students in a class. c) The scores you receive on the first midterm, s
> True or False. If False, explain briefly. a) We choose the linear model that passes through the most data points on the scatterplot. b) The residuals are the observed y-values minus the y-values predicted by the linear model. c) Least squares means that
> For the following experiment, indicate whether it was single-blind, double-blind, or not blinded at all. Explain your reasoning. Does a “stop smoking” program work better if it costs more? Smokers responding to an advertisement offering to help them stop
> A study finds that during blizzards, online sales are highly associated with the number of snow plows on the road; the more plows, the more online purchases. The director of an association of online merchants suggests that the organization should encoura
> A larger firm is considering acquiring the bookstore of Exercise 1. An analyst for the firm, noting the relationship seen in Exercise 1, suggests that when they acquire the store they should hire more people because that will drive higher sales. Is his c
> If we assume that the conditions for correlation are met, which of the following are true? If false, explain briefly. a) A correlation of 0.02 indicates a strong positive association. b) Standardizing the variables will make the correlation 0. c) Addi
> If we assume that the conditions for correlation are met, which of the following are true? If false, explain briefly. a) A correlation of -0.98 indicates a strong, negative association. b) Multiplying every value of x by 2 will double the correlation.
> A company that relies on Internet-based advertising linked to key search terms wants to understand the relationship between the amount it spends on this advertising and revenue (in $). a) Which variable is the explanatory or predictor variable? b) Whic
> The human resources department at a large multinational corporation wants to be able to predict average salary for a given number of years’ experience. Data on salary (in $1000s) and years of experience were collected for a sample of employees. a) Which
> An online investment blogger advises investing in mutual funds that have performed badly the past year because “regression to the mean tells us that they will do well next year.” Is he correct?
> A CEO complains that the winners of his “rookie junior executive of the year” award often turn out to have less impressive performance the following year. He wonders whether the award actually encourages them to slack off. Can you offer a better explanat
> For the disk drives in Exercise 2, we want to predict Price from Capacity. a) Find the slope estimate, b1 and interpret it in words. b) Does the slope seem reasonable? Explain. c) Find the intercept, b0. d) What does it mean, in this context? Is it meani
> For the following experiment, indicate whether it was single-blind, double-blind, or not blinded at all. Explain your reasoning. Makers of a new frozen entrée arranged for it to be served to randomly selected customers at a restaurant in place of the equ
> For the bookstore of Exercise 1, the manager wants to predict Sales from Number of Sales People Working. a) Find the slope estimate, b1. b) What does it mean, in this context? c) Find the intercept, b0. d) What does it mean, in this context? Is it meanin
> For the hard drive data in Exercise 2, the correlation is 0.988 and other summary statistics are: a) If a drive has a capacity of 17.46 TB (or 1 SD above the mean), how many standard deviations above or below the mean price of $785.82 do you expect the
> For the bookstore sales data in Exercise 1, the correlation of number of sales people and sales is 0.965. a) If the number of people working is 2 standard deviations above the mean, how many standard deviations above or below the mean do you expect sales
> True or False. If False, explain briefly. a) Some of the residuals from a least squares linear model will be positive and some will be negative. b) Least Squares means that some of the squares of the residuals are minimized. c) We write y^ to denote the
> Consider the following data from a small bookstore. a) Prepare a scatterplot of Sales against Number of Sales People Working. b) What can you say about the direction of the association? c) What can you say about the form of the relationship? d) What ca
> The histogram shows the December charges (in $) for 5000 customers from one marketing segment from a credit card company. (Negative values indicate customers who received more credits than charges during the month.) a) Write a short description of this d
> For the data in Exercise 2: a) Find the quartiles using your calculator. b) Find the quartiles using the Tukey method (page 65). c) Find the IQR using the quartiles from part b. d) Find the standard deviation. Exercise 2: As the new manager of a small c
> For the data in Exercise 1: a) Find the quartiles using your calculator. b) Find the quartiles using the Tukey method (page 65). c) Find the IQR using the quartiles from part b. d) Find the standard deviation.
> Jeff, a sales manager of a car dealership, believes that his sales force sells a car to 35% of the customers who stop by the showroom. He needs the dealership to make 50 sales this month to get a special bonus of $100,000. Approximately 120 customers vis
> Suppose the archer from Exercise 58 shoots 10 arrows. a) Find the mean and standard deviation of the number of bull’s-eyes she may get. b) What’s the probability that she never misses? c) What’s the probability that there are no more than 8 bull’s-eyes?
> Analysts from the Internet company of Exercise 5 are now concerned that customers who come directly to their site (by typing their URL into a browser) might respond differently than those referred to the site from other sites (such as search engines). Th
> Suppose we choose 12 people instead of the 5 chosen in Exercise 57. a) Find the mean and standard deviation of the number of right-handers in the group. b) What’s the probability that they’re not all right-handed? c) What’s the probability that there
> Consider our archer from Exercise 52. a) How many bull’s-eyes do you expect her to get? b) With what standard deviation? c) If she keeps shooting arrows until she hits the bull’s-eye, how long do you expect it will take?
> Consider our group of 5 people from Exercise 51. a) How many lefties do you expect? b) With what standard deviation? c) If we keep picking people until we find a lefty, how long do you expect it will take?
> The manufacturer in Exercise 54 has noticed that the number of faulty cell phones in a production run of cell phones is usually small and that the quality of one day’s run seems to have no bearing on the next day. a) What model might you use to model th
> A website manager has noticed that during the evening hours, about 3 people per minute check out from their shopping cart and make an online purchase. She believes that each purchase is independent of the others and wants to model the number of purchases
> The scatterplot shows, for 2015 cars, the carbon footprint (tons of CO2 per mile) vs. the new Environmental Protection Agency (EPA) highway mileage for 69 family sedans as reported by the U.S. government (www.fueleconomy.gov/feg/byclass.htm); the cars in
> At a small company, the head of human resources wants to examine salary to prepare annual reviews. He selects 28 employees at random with job types ranging from 01 = Stocking clerk to 99 = President. He plots Salary ($) against Job Type and finds a stron
> A sales manager for a major pharmaceutical company analyzes last year’s sales data for her 96 sales representatives, grouping them by region (1 = East Coast United States; 2 = Mid West United States; 3 = West United States; 4 = South Un
> Insurance companies carefully track claims histories so that they can assess risk and set rates appropriately. The National Insurance Crime Bureau reports that Honda Accords, Honda Civics, and Toyota Camrys are the cars most frequently reported stolen, w
> A CEO announces at the annual shareholders meeting that the new see-through packaging for the company’s flagship product has been a success. In fact, he says, “There is a strong correlation between packaging and sales.” Criticize this statement on statis
> In an effort to check the quality of their cell phones, a manufacturing manager decides to take a random sample of 10 cell phones from yesterday’s production run, which produced cell phones with serial numbers ranging (according to when they were produce
> The 30 quarterbacks in Exercise 32 had an average Salary of $13,788,022 1SD = $8,130,5362. The correlation between Salary and Total QBR = 0.278. If a player had a Total QBR rating 1 SD below the average, what Salary would you predict for it? Exercise 32
> For the data in Exercise 31, the average Sales was 52,697 pounds (SD = 10,261 pounds), and the correlation between Price and Sales was = -0.547. If the Price in a particular week was one SD higher than the mean Price, how much pizza would you predict was
> In 2016, the Los Angeles Dodgers spent nearly one quarter billion (!) dollars on salaries for their players (Spotrac). Is there a relationship between salary and team performance in Major League Baseball? For the 2016 season, a linear model fit to the nu
> Is there a relationship between total team salary and the performance of teams in the National Football League (NFL)? For the 2016–2017 season, a linear model predicting Wins (out of 16 regular season games) from the total team Salary ($M) for the 32 tea
> Quarterback performance 2017. The average salary for 30 top NFL quarterbacks in 2017 was just over $13,000,000. A linear model to predict Salary from Total QBR (an overall measure of performance based on game statistics) found the following: a) What i
> A linear model fit to predict weekly Sales of frozen pizza (in pounds) from the average Price ($/unit) charged by a sample of stores in the city of Dallas in 39 recent weeks is: (Data in Pizza prices) a) What is the explanatory variable? b) What is t
> Here are several scatterplots. The calculated correlations are -0.977, -0.021, 0.736, and 0.951. Which is which? (a) (b) (c) (d)
> Here are several scatterplots. The calculated correlations are -0.923, -0.487, 0.006, and 0.777. Which is which? (a) (b) (c) (d)
> Owners of a new coffee shop tracked sales for the first 20 days and displayed the data in a scatterplot a) Make a histogram of the daily sales since the shop has been in business. b) State one fact that is obvious from the scatterplot, but not from the
> A ceramics factory can fire eight large batches of pottery a day. Sometimes a few of the pieces break in the process. In order to understand the problem better, the factory records the number of broken pieces in each batch for three days and then creates
> A cable provider wants to contact customers in a particular telephone exchange to see how satisfied they are with the new digital TV service the company has provided. All numbers are in the 452 exchange, so there are 10,000 possible numbers from 452-0000
> Which of the scatterplots show: a) Little or no association? b) A negative association? c) A linear association? d) A moderately strong association? e) A very strong association? (1) [:.. (3) (4)
> Which of the scatterplots show: a) Little or no association? b) A negative association? c) A linear association? d) A moderately strong association? e) A very strong association? (1) (3) (4)
> Suppose you were to collect data for each pair of variables. You want to make a scatterplot. Which variable would you use as the explanatory variable and which as the response variable? Why? What would you expect to see in the scatterplot? Discuss the li
> Suppose you were to collect data for each pair of variables. You want to make a scatterplot. Which variable would you use as the explanatory variable and which as the response variable? Why? What would you expect to see in the scatterplot? Discuss the li
> The Toy Association tracks sales of toys using a tracking survey that represents approximately 80% of U.S. toy sales. Projected to the entire industry, the following table breaks down U.S. toy sales by category. a) Create an appropriate graphical display
> In 2014, Pew Research Center released the results of a survey among U.S. adults that asked nearly 2000 people how satisfied they are with their current financial situation (www.pewsocialtrends .org/datasets/). Responses were collected by gender, using a
> An insurance company is updating its payouts and cost structure for their insurance policies. Of particular interest to them is the risk analysis for customers currently on heart or blood pressure medication. The Centers for Disease Control and Preventio
> Here’s a pie chart of the data in Exercise 16. a) Which display of these data is best for comparing the market value of these brands? Explain. b) Does Pepsi or Red Bull have a larger market value? Is that comparison easier to make wit
> Here’s a bar chart of the data in Exercise 15. a) Compared to the pie chart in Exercise 15, which is better for displaying the relative portions of market share? Explain. b) What is missing from this display that might make it somewha
> An Olympic archer is able to hit the bull’seye 80% of the time. Assume each shot is independent of the others. If she shoots 6 arrows, what’s the probability of each of the following results? a) Her first bull’s-eye comes on the third arrow. b) She mis
> Tuition 2016. In 2016, the mean tuition of private colleges and universities was $18,230, with a standard deviation of $7272. The mean tuition for public colleges and universities was $9624, with a standard deviation of $4669. The distribution of tuition
> The 1057 houses described in Exercise 44 have a mean price of $167,900, with a standard deviation of $77,158. The mean living area is 1819 sq. ft., with a standard deviation of 663 sq. ft. Which is more unusual, a house in that market that sells for $400
> A second report by the National Center for Productivity analyzed the relationship between productivity and wages. They used the graph from Exercise 67, with the x-axis labeled “wages.” Comment on any problems you see with their analysis.
> The National Center for Productivity releases information on the efficiency of workers. In a recent report, they included the following graph showing a rapid rise in productivity. What questions do you have about this? 3.5 2.5 Productivity

