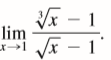Question: Evaluate /
> Evaluate the limit and justify each step by indicating the appropriate Limit Law(s). lim (x* – 3x)(x² + 5x + 3) -1
> Evaluate the limit and justify each step by indicating the appropriate Limit Law(s). lim (5x* - 3x? + х — 6)
> The figure shows a fixed circle C1 with equation (x – 1)2 + y2 − 1 and a shrinking circle C2 with radius r and center the origin. P is the point (0, r), Q is the upper point of intersection of the two circles, and R is
> Is there a number a such that exists? If so, find the value of a and the value of the limit. 3x? Зx2 + ах + а +3 lim x→-2 х2 +x — 2
> Evaluate / 6 – x – 2/ 3 – x – 1.
> Explain what it means to say that In this situation is it possible that limx → 1 f(x) exists? Explain. lim f(x) = 3 and lim f(x) = 7 %3D
> Explain in your own words what is meant by the equation Is it possible for this statement to be true and yet f(2) = 3? Explain. lim f(x) = 5
> For the function f whose graph is shown, state the following. f. The equations of the vertical asymptotes. (a) lim f(x) (b) lim f(x) (c) lim f(x) X-7 X-3 (d) lim f(x) (e) lim f(x) X6+ y -7 6 3.
> For the function g whose graph is given, state the value of each quantity, if it exists. If it does not exist, explain why. (a) lim g(t) (b) lim g(t) (c) lim g(t) 0 (d) lim g(t) (e) lim g(t) 2+ (f) lim g(t) 2 (g) g(2) (h) lim g(t) 4 -2 4 2. 4,
> If a rock is thrown upward on the planet Mars with a velocity of 10 m/s, its height in meters t seconds later is given by y = 10t - 1.86t2. a. Find the average velocity over the given time intervals: i. [1, 2] ii. [1, 1.5] iii. [1, 1.1] iv. [1, 1.01
> For the function h whose graph is given, state the value of each quantity, if it exists. If it does not exist, explain why. (a) lim h(x) X-3 (b) X-3+ lim h(x) (c) lim_h(x) X-3 (d) h(-3) (e) lim h(x) (f) lim h(x) X0+ (g) lim h(x) (h) h(0) (i) lim h
> For the function f whose graph is given, state the value of each quantity, if it exists. If it does not exist, explain why. (a) lim f(x) (b) lim f(x) X3 (c) lim f(x) X3+ (d) lim f(x) (e) ƒ(3) y. 4 2 4 2.
> Use the given graph off to state the value of each quantity, if it exists. If it does not exist, explain why. (a) lim f(x) (b) lim f(x) (c) lim f(x) (d) f(2) (e) lim f(x) (f) f(4) 4 4 2. 2.
> Explain the meaning of each of the following. (a) lim f(x) = (b) lim f(x) X-3 X4+
> a. Use numerical and graphical evidence to guess the value of the limit b. How close to 1 does x have to be to ensure that the function in part (a) is within a distance 0.5 of its limit? x - 1 lim →1 Vx – 1
> For the function A whose graph is shown, state the following. e. The equations of the vertical asymptotes (a) lim A(x) (b) lim A(x) X2 X-3 (c) lim A(x) X2+ (d) lim A(x) -3 5 2.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If limx → 5 f(x) = 2 and limx → 5 g(x) = 0, then limx → 5 [f(x)/g(x)] does not exist.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. x? – 9 lim X-3 x - 3 lim (x + 3) X-
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. x2 – 9/x - 3 = x + 3
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. lim (x – 3) x – 3 lim l x? + 2x – 4 lim (x? + 2x – 4)
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. lim (x? + 6х — 7) х? + 6х — 7 lim х>і x? + 5х — 6 lim (x? + 5x – 6)
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. 2x lim X4 x - 4 2x 8 lim x→4x - 4 8 lim X4 X - 4 x - 4
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If | f | is continuous at a, so is f.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f is continuous at a, so is | f |.
> In the theory of relativity, the mass of a particle with velocity v is where m0 is the mass of the particle at rest and c is the speed of light. What happens as v → c-? mo m = V1 - v²/c²
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. The equation x10 - 10x2 + 5 = 0 has a root in the interval (0, 2).
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. d2y/dx2=(dy/dx)2
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f’(r) exists, then limx → r f(x) = f(r).
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f is continuous at a, then f is differentiable at a.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f(x) > 1 for all x and limx→0 f(x) exists, then limx→0 f(x) > 1.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. Let f be a function such that limx→0 f(x) = 6. Then there exists a positive number δ such that if 0
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f is continuous on [-1, 1] and f(-1) = 4 and f(1) = 3, then there exists a number r such that |r
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f is continuous at 5 and f(5) = 2 and f(4) = 3, then limx → 2 f(4x2 – 11) = 2.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f(1) > 0 and f(3) < 0, then there exists a number c between 1 and 3 such that f(c) = 0.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If the line x = 1 is a vertical asymptote of y = f(x), then f is not defined at 1.
> Use a graph to estimate the equations of all the vertical asymptotes of the curve y = tan(2sinx) -π ≤ x ≤ π Then find the exact equations of these asymptotes.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f has domain (0, ∞) and has no horizontal asymptote, then lim x → ∞ f(x) = ∞ or limx → ∞ f(x) =
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. A function can have two different horizontal asymptotes.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If limx → 0 f(x) = ∞ and limx → 0 g(x) = ∞, then limx → 0 [f(x) - g(x)] = 0.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If p is a polynomial, then limx → b p(x) = p(b).
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If limx → 6 [f(x)g(x)] exists, then the limit must be f(6)g(6).
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If limx → a f(x) exists but limx → a g(x) does not exist, then limx → a[f(x) + g(x)] does not exist
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If neither limx → a f(x) nor limx → a g(x) exists, then limx → a [f(x) + g(x)] does not exist.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If limx→5 f(x) = 0 and limx → 5 g(x) = 0, then limx → 5 [f(x)/g(x)] does not exist.
> Evaluate the following limits, if they exist, where [[x]] denotes the greatest integer function. [x] (а) lim (b) lim x [1/x]
> The figure shows a point P on the parabola y = x2 and the point Q where the perpendicular bisector of OP intersects the y-axis. As P approaches the origin along the parabola, what happens to Q? Does it have a limiting position? If so, find it.
> Consider the function f(x) = tan/x. a. Show that f(x) = 0 for x = 1/Ï€ , 1/2Ï€, 1/3Ï€ , ... b. Show that f(x) = 1 for x = 4/Ï€ , 4/5Ï€ , 4/9Ï€, ... c. What can you conclude about 1 lim tan
> Evaluate | 2x – 1| – |2x + 1| lim
> Find numbers a and b such that Vax + b – 2 lim 1.
> Suppose f is a function that satisfies the equation f(x + y) = f(x) + f(y) + x2y + xy2 for all real numbers x and y. Suppose also that a. Find f(0). b. Find f’(0). c. Find f’(x). S(x) lim X-0 X 1
> If f is a differentiable function and g(x) = xf(x), use the definition of a derivative to show that g’(x) = xf’(x) + f(x).
> a. If we start from 0° latitude and proceed in a westerly direction, we can let T(x) denote the temperature at the point x at any given time. Assuming that T is a continuous function of x, show that at any fixed time there are at least two diametrically
> If limx → a [f(x) + g(x)] = 2 and limx → a [f(x) – g(x)] = 1, find limx → a [f(x)g(x)].
> A fixed point of a function f is a number c in its domain such that f(c) = c. (The function doesn’t move c; it stays fixed.) a. Sketch the graph of a continuous function with domain [0, 1] whose range also lies in [0, 1]. Locate a fixed point of f. b.
> Find all values of a such that f is continuous on R: x + 1 if x< a x² S(x) = if x>a
> Graph the function f(x) = sin(π/x) of Example 4 in the viewing rectangle [-1, 1] by [-1, 1]. Then zoom in toward the origin several times. Comment on the behavior of this function.
> Sketch the region in the plane defined by each of the following equations. (a) [x]? + [[y]² = 1 (c) [x + y]? = 1 (b) [x]? – [y]? = 3 (d) [x] + [y] = 1
> Find the limit. x² – 9 lim -3 x? + 2x – 3
> Find the limit. lim e31 K.
> Sketch the graph of a function f that satisfies all of the following conditions: f is continuous from the right at 3 lim f(x) = -2, lim f(x) = 0, lim f(x) = ∞, X-3 lim f(x) = -0∞, X3- lim f(x) = 2, X→3+
> The graph of f is given. a. Find each limit, or explain why it does not exist. b. State the equations of the horizontal asymptotes. c. State the equations of the vertical asymptotes. d. At what numbers is f discontinuous? Explain. (i) lim f(x)
> Let a. For what values of a does limx→a f(x) exist? b. At what numbers is f discontinuous? f(x) = [x] + [-x].
> Suppose that |f(x)|≤ g(x) for all x, where limx→a g(x) = 0. Find limx→a f(x).
> The total fertility rate at time t, denoted by F(t), is an estimate of the average number of children born to each woman (assuming that current birth rates remain constant). The graph of the total fertility rate in the United States shows the fluctuation
> Let B(t) be the number of US $20 bills in circulation at time t. The table gives values of this function from 1990 to 2010, as of December 31, in billions. Interpret and estimate the value of B’(2000). 1990 1995 2000 2005 2010 B(t)
> Let P(t) be the percentage of Americans under the age of 18 at time t. The table gives values of this function in census years from 1950 to 2010. a. What is the meaning of P’(t)? What are its units? b. Construct a table of estimated
> a. Evaluate h(x) = (tan x - x)/x3 for x = 1, 0.5, 0.1, 0.05, 0.01, and 0.005. b. Guess the value of c. Evaluate h(x) for successively smaller values of x until you finally reach a value of 0 for h(x). Are you still confident that your guess in part (b)
> If a ball is thrown into the air with a velocity of 40 ft/s, its height in feet t seconds later is given by y = 40t - 16t2. a. Find the average velocity for the time period beginning when t = 2 and lasting i. 0.5 seconds ii. 0.1 seconds iii. 0.05 sec
> Sketch the graph of a function f that satisfies all of the following conditions: The domain of f is all real numbers except 0, / for all x in the domain of f/
> The figure shows the graphs of f, f’, and f’’. Identify each curve, and explain your choices. y. a b
> The graph of f is shown. State, with reasons, the numbers at which f is not differentiable. y 2 4 6.
> a. Find the asymptotes of the graph of f(x) = 4 – x/3 + x and use them to sketch the graph. b. Use your graph from part (a) to sketch the graph of f’. c. Use the definition of a derivative to find f’(x). d. Use a graphing device to graph f’ and compa
> a. If f(x) = 3− 5x , use the definition of a derivative to find f9sxd. b. Find the domains of f and f’. c. Graph f and f’ on a common screen. Compare the graphs to see whether your answer to part (a) is reasonable.
> Trace or copy the graph of the function. Then sketch a graph of its derivative directly beneath.
> Trace or copy the graph of the function. Then sketch a graph of its derivative directly beneath. yA
> Trace or copy the graph of the function. Then sketch a graph of its derivative directly beneath. yA
> The total cost of repaying a student loan at an interest rate of r% per year is C = f(r). a. What is the meaning of the derivative f’(r)? What are its units? b. What does the statement f’(10) = 1200 mean? c. Is f’(r) always positive or does it change s
> Find a function f and a number a such that (2 + h)* – 64 lim = f'(a) h
> a. Evaluate the function f(x) = x2 – (2x/1000) for x = 1, 0.8, 0.6, 0.4, 0.2, 0.1, and 0.05, and guess the value of b. Evaluate f(x) for x = 0.04, 0.02, 0.01, 0.005, 0.003, and 0.001. Guess again. 2* lim x² 1000
> a. Use the definition of a derivative to find f’(2), where f(x) = x3 - 2x. b. Find an equation of the tangent line to the curve y = x3 - 2x at the point (2, 4). c. Illustrate part (b) by graphing the curve and the tangent line on the same screen.
> According to Boyle’s Law, if the temperature of a confined gas is held fixed, then the product of the pressure P and the volume V is a constant. Suppose that, for a certain gas, PV = 800, where P is measured in pounds per square inch and V is measured in
> The displacement (in meters) of an object moving in a straight line is given by s = 1 + 2t + 1/4t2, where t is measured in seconds. a. Find the average velocity over each time period. i. [1, 3] ii. [1, 2] iii. [1, 1.5] iv. [1, 1.1] b. Find the i
> Find equations of the tangent lines to the curve y = 2/ 1 - 3x at the points with x-coordinates 0 and -1.
> a. Find the slope of the tangent line to the curve y = 9 - 2x2 at the point (2, 1). b. Find an equation of this tangent line.
> Use the Intermediate Value Theorem to show that there is a root of the equation in the given interval. cos√x = ex - 2, (0, 1)
> Use the Intermediate Value Theorem to show that there is a root of the equation in the given interval. x5 - x3 + 3x - 5 = 0, (1, 2)
> Show that the function is continuous on its domain. State the domain. g(x) = x2 – 9 /x2 - 2
> Show that the function is continuous on its domain. State the domain. h(x) = xesinx
> Let a. For each of the numbers 2, 3, and 4, discover whether g is continuous from the left, continuous from the right, or continuous at the number. b. Sketch the graph of g. 2х — х2 if 0 <x<2 2 — х if 2<x<3 g(x) · х — 4 if 3<x< 4 IT if x>4
> a. Graph the function f(x) = ex + ln|x - 4| for 0 ≤ x ≤ 5. Do you think the graph is an accurate representation off ? b. How would you get a graph that represents f better?
> Let a. Evaluate each limit, if it exists. b. Where is f discontinuous? c. Sketch the graph of f. if x<0 fx) — { 3 — х if 0 <x<3 (х — 3)? if x >3 (i) lim f(x) (ii) lim f(x) (iii) lim f(x) (iv) lim f(x) (v) lim f(x) (vi) lim f(x)
> Prove the statement using the precise definition of a limit. 2 lim 'x – 4 00
> Prove the statement using the precise definition of a limit. lim (x? — Зx) —-2
> Prove the statement using the precise definition of a limit. lim Vx = 0 %3D
> Prove the statement using the precise definition of a limit. lim (14 – 5x) = 4
> Prove that limx → 0 x2 cos(1/x2) = 0.
> If 2x - 1 ≤ f(x) ≤ x2 for 0 < x < 3, find limx →1 f(x).
> Use graphs to discover the asymptotes of the curve. Then prove what you have discovered. y = x2 + x + 1 - x2 − x
> Use graphs to discover the asymptotes of the curve. Then prove what you have discovered. y = cos2x/x2
> Find the limit. 1 lim - 1 x? — Зх + 2