Question: Evaluate the function at the given value(
Evaluate the function at the given value(s) of the independent variable. Then find the domain and range.
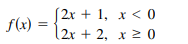
a. f (−1)
b. f (0)
c. f (2)
d. f (t2 + 1)
> Use a graphing utility to graph the equation. Move the cursor along the curve to approximate the unknown coordinate of each solution point accurate to two decimal places. y = x5 − 5x (−0.5, y) (x, −4)
> Sketch a graph of the function and find its domain and range. Use a graphing utility to verify your graph. f (x) = x2 + 5
> Sketch the graph of the function. y = 2 tan x
> Sketch the graph of the function. y = -sin 2πx/3
> Sketch the graph of the function. y = sin x/2
> Sketch the graph of the function. y = sin x/2
> Use a graphing utility to graph each function f in the same viewing window for c = −2, c = −1, c = 1, and c = 2. Give a written description of the change in the graph caused by changing c. a. f(x) = sin x + c b. f(x) = -sin (2πx - c) c. f(x) = c cos x
> Use a graphing utility to graph each function f in the same viewing window for c = −2, c = −1, c = 1, and c = 2. Give a written description of the change in the graph caused by changing c. a. f(x) = c sin x b. f(x) = cos(cx) c. f(x) = cos(πx − c)
> Find the period of the function. y = csc 4x
> Find the period of the function. y = sec 5x
> Find the period of the function. y = 7 tan 2πx
> Use a graphing utility to graph the equation. Move the cursor along the curve to approximate the unknown coordinate of each solution point accurate to two decimal places. y = √5 − x (2, y) (x, 3)
> Find the period of the function. y = 5 tan 2x
> Sketch a graph of the function and find its domain and range. Use a graphing utility to verify your graph. f (x) = 4 − x
> Determine the period and amplitude of each function. y = 2/3 cos πx/10
> Determine the period and amplitude of each function. y = −3 sin 4πx
> Determine the period and amplitude of each function. y = 3/2 cos x/2
> Determine the period and amplitude of each function. y = 2 sin 2x
> While traveling across flat land, you notice a mountain directly in front of you. Its angle of elevation (to the peak) is 3.5°. After you drive 13 miles closer to the mountain, the angle of elevation is 9°. Approximate the height of
> An airplane leaves the runway climbing at an angle of 18° with a speed of 275 feet per second (see figure). Find the altitude a of the plane after 1 minute.
> Solve the equation for θ, where 0 ≤ θ ≤ 2π. cos θ/2 - cos θ = 1
> Solve the equation for θ, where 0 ≤ θ ≤ 2π. cos2 θ + sin θ = 1
> Sketch the graph of the equation by point plotting. y = 1 / x + 2
> Solve the equation for θ, where 0 ≤ θ ≤ 2π. sin θ = cos θ
> Solve the equation for θ, where 0 ≤ θ ≤ 2π. sec θ csc θ = 2 csc θ
> Evaluate the function at the given value(s) of the independent variable. Then find the domain and range. a. f (−3) b. f (1) c. f (3) d. f (b2 + 1)
> Solve the equation for θ, where 0 ≤ θ ≤ 2π. 2 cos2 θ –cos θ = 1
> Solve the equation for θ, where 0 ≤ θ ≤ 2π. tan2 θ –tan θ = 0
> Solve the equation for θ, where 0 ≤ θ ≤ 2π. tan2 θ = 3
> Solve the equation for θ, where 0 ≤ θ ≤ 2π. 2 sin2 θ = 1
> Find two solutions of each equation. Give your answers in radians (0 ≤ θ ≤ 2π). Do not use a calculator. a. sin θ = √3/2 b. sin θ = -√3/2
> Find two solutions of each equation. Give your answers in radians (0 ≤ θ ≤ 2π). Do not use a calculator. a. tan θ = 1 b. cot θ = -√3
> Find two solutions of each equation. Give your answers in radians (0 ≤ θ ≤ 2π). Do not use a calculator. a. sec θ = 2 b. sec θ = -2
> Sketch the graph of the equation by point plotting. y = 3/x
> Find two solutions of each equation. Give your answers in radians (0 ≤ θ ≤ 2π). Do not use a calculator. a. cos θ = √2/2 b. cos θ = -√2/2
> Determine the quadrant in which θ lies. a. sin θ > 0 and cos θ < 0 b. csc θ < 0 and tan θ > 0
> Determine the quadrant in which θ lies. a. sin θ < 0 and cos θ < 0 b. sec θ > 0 and cot θ < 0
> Evaluate the function at the given value(s) of the independent variable. Then find the domain and range. a. f (−2) b f (0) c. f (1) d. f (s2 + 2)
> Use a calculator to evaluate each trigonometric function. Round your answers to four decimal places. a. cot(1.35) b. tan(1.35)
> Use a calculator to evaluate each trigonometric function. Round your answers to four decimal places. a. tan π/9 b. tan 10π/9
> Use a calculator to evaluate each trigonometric function. Round your answers to four decimal places. a. sec 225° b. sec 135º
> Use a calculator to evaluate each trigonometric function. Round your answers to four decimal places. a. sin 10° b. csc 10º
> Evaluate the sine, cosine, and tangent of each angle. Do not use a calculator. a. 750º b. 510º c. 10π/3 d. 17π/3
> Sketch the graph of the equation by point plotting. y = √x + 2
> Evaluate the sine, cosine, and tangent of each angle. Do not use a calculator. a. 225º b. -225º c. 5π/3 d. 11π/6
> Evaluate the sine, cosine, and tangent of each angle. Do not use a calculator. a. -30º b. 150º c. -π/6 c. π/2
> Evaluate the sine, cosine, and tangent of each angle. Do not use a calculator. a. 60º b. 120º c. π/4 d. 5π/4
> Sketch a right triangle corresponding to the trigonometric function of the acute angle θ. Then evaluate the other five trigonometric functions of θ. sec θ = 13/5
> Sketch a right triangle corresponding to the trigonometric function of the acute angle θ. Then evaluate the other five trigonometric functions of θ. cos θ = 4/5
> Sketch a right triangle corresponding to the trigonometric function of the acute angle θ. Then evaluate the other five trigonometric functions of θ. sin θ = 1/3
> Sketch a right triangle corresponding to the trigonometric function of the acute angle θ. Then evaluate the other five trigonometric functions of θ. sin θ = 1/2
> Evaluate the six trigonometric functions of the angle θ. a. / b. /
> Evaluate the six trigonometric functions of the angle θ.
> Sketch the graph of the equation by point plotting. y = √x - 6
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If f is a function, then f(ax) = af(x).
> A car is moving at the rate of 50 miles per hour, and the diameter of its wheels is 2.5 feet. a. Find the number of revolutions per minute that the wheels are rotating. b. Find the angular speed of the wheels in radians per minute.
> Let r represent the radius of a circle, θ the central angle (measured in radians), and s the length of the arc subtended by the angle. Use the relationship s = rθ to complete the table.
> Convert the radian measure to degree measure. a. 7π / 3 b. –(11π / 30) c. 11π / 6 d. 0.438
> Convert the radian measure to degree measure. a. 3π / 2 b. 7π / 6 c. –(7π / 12) d. -2.367
> Convert the degree measure to radian measure as a multiple of π and as a decimal accurate to three decimal places. a. -20º b. -240º c. -270º d. 144º
> Convert the degree measure to radian measure as a multiple of π and as a decimal accurate to three decimal places. a. 30º b. 150º c. 315º d. 120º
> find the domain of the function. g(x) = 1 / │x2 - 4│
> Determine two co-terminal angles in radian measure (one positive and one negative) for each angle. a. / b. /
> Determine two co-terminal angles in radian measure (one positive and one negative) for each angle. a. / b. /
> Determine two co-terminal angles in degree measure (one positive and one negative) for each angle. a. / b. /
> Sketch the graph of the equation by point plotting. y = │x│ - 1
> Determine two co-terminal angles in degree measure (one positive and one negative) for each angle. a. / b. /
> In your own words, describe the meaning of amplitude and period.
> Find sin θ, cos θ, and tan θ.
> Explain how to convert from degrees to radians.
> Explain how to find co-terminal angles in degrees.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If a line contains points in both the first and third quadrants, then its slope must be positive.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. The lines represented by ax + by = c1 and bx – ay = c2 are perpendicular. Assume a ≠ 0 and b ≠ 0.
> Find the domain of the function. f(x) = 1 / │x + 3│
> Prove that if the slopes of two non-vertical lines are negative reciprocals of each other, then the lines are perpendicular.
> Prove that if the points (x1, y1) and (x2, y2) lie on the same line as (x1∗, y1∗) and (x2∗, y2∗), then Assume x1 ≠x2 and x1∗ â‰
> Sketch the graph of the equation by point plotting. y = │x + 1│
> Prove that the figure formed by connecting consecutive midpoints of the sides of any quadrilateral is a parallelogram.
> Prove that the diagonals of a rhombus intersect at right angles. (A rhombus is a quadrilateral with sides of equal lengths.)
> Use the result below to find the distance between the point and line. Point: (2, 3) Line: 4x + 3y = 10
> Use the result below to find the distance between the point and line. Point: (−2, 1) Line: x − y − 2 = 0
> Write the distance d between the point (3, 1) and the line y = mx + 4 in terms of m. Use a graphing utility to graph the equation. When is the distance 0? Explain the result geometrically.
> Show that the distance between the point (x1, y1) and the line Ax + By + C = 0 is Distance = /
> An instructor gives regular 20-point quizzes and 100-point exams in a mathematics course. Average scores for six students, given as ordered pairs (x, y), where x is the average quiz score and y is the average exam score, are (18, 87), (10, 55), (19, 96),
> A real estate office manages an apartment complex with 50 units. When the rent is $780 per month, all 50 units are occupied. However, when the rent is $825, the average number of occupied units drops to 47. Assume that the relationship between the monthl
> Find the domain of the function. f(x) = √x2 − 3x + 2
> As a salesperson, you receive a monthly salary of $2000, plus a commission of 7% of sales. You are offered a new job at $2300 per month, plus a commission of 5% of sales. Write linear equations for your monthly wage W in terms of your monthly sales s for
> Sketch the graph of the equation by point plotting. y = (x − 3)2
> Find a linear equation that expresses the relationship between the temperature in degrees Celsius C and degrees Fahrenheit F. Use the fact that water freezes at 0°C (32°F) and boils at 100°C (212°F). Use the equation to convert 72°F to degrees Celsius.
> Several lines are shown in the figure below. (The lines are labeled a–f.) a. Which lines have a positive slope? b. Which lines have a negative slope? c. Which lines appear parallel? d. Which lines appear perpendicular?
> Find the coordinates of the point of intersection of the given segments. Explain your reasoning. a. Perpendicular bisectors b. Medians
> Find an equation of the line tangent to the circle (x − 1)2 + (y − 1)2 = 25 at the point (4, −3).
> Find an equation of the line tangent to the circle x2 + y2 = 169 at the point (5, 12).
> A line is represented by the equation ax + by = 4. When is the line parallel to the x-axis? When is the line parallel to the y-axis? Give values for a and b such that the line has a slope of 5/8. Give values for a and b such that the line is perpendicula
> Show that the points (−1, 0), (3, 0), (1, 2), and (1, −2) are vertices of a square.
> Determine whether the points are collinear. (Three points are collinear if they lie on the same line.) (0, 4), (7, -6), (-5, 11)
> Determine whether the points are collinear. (Three points are collinear if they lie on the same line.) (-2, 1), (-1, 0), (2, -2)
> Find the domain of the function. f(x) = √x + √1 − x
> You are given the dollar value of a product in 2016 and the rate at which the value of the product is expected to change during the next 5 years. Write a linear equation that gives the dollar value V of the product in terms of the year t. (Let t = 0 repr
> You are given the dollar value of a product in 2016 and the rate at which the value of the product is expected to change during the next 5 years. Write a linear equation that gives the dollar value V of the product in terms of the year t. (Let t = 0 repr

