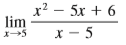Question: Evaluate the limit, if it exists. /

> Evaluate the types of retrenchment strategies that might be used by companies in stagnant industries.

> List the means available to a company for horizontal growth and explain why a company might pursue one over another.

> What is the value of portfolio analysis? Its dangers?

> Must a corporation have a common thread running through its many activities in order to be successful? Why or why not?

> How does transaction cost economics apply to vertical growth? To concentric versus conglomerate diversification?

> How can a company overcome the limitations of being in a fragmented industry?

> Why should information systems be included in the analysis of a corporation’s strengths and weaknesses?

> What kind of internal factors help managers determine whether a firm should emphasize the production and sales of a large number of low-priced products or a small number of high-priced products?

> What recommendations would you make to improve the effectiveness of today’s boards of directors?

> Is benchmarking just another fad or is it really useful for all firms? Why?

> Why bother with shareholder value or a stakeholder scorecard? Isn’t it simpler to evaluate a corporation and its SBUs just by using standard measures such as ROI or earnings per share?

> How can MBO help improve the implementation of strategy?

> How does a hypercompetitive environment change the strategic approach for a company?

> What value does a total quality management program have in implementing strategy?

> Compare and contrast action planning with management by objectives.

> Does culture follow strategy or does strategy follow culture? Why?

> How might manager–strategy fit be accomplished short of firing current managers?

> Does structure follow strategy or does strategy follow structure? Why?

> Japanese corporations typically involve many more organizational levels and people in the development of implementation plans than do U.S. corporations. Is this appropriate? Why or why not?

> Should functional strategies be categorized under strategy formulation or under strategy implementation?

> What are the advantages and disadvantages of the devil’s advocate, dialectical inquiry, and consensus approaches to making strategic choices?

> What are the pros and cons of technological leader versus technological follower as a functional strategy?

> What concepts or assumptions underlie the BCG growth-share matrix? Are these concepts valid? Why or why not?

> Explain how using an IFAS Table impacts the understanding of a company’s internal resources and capabilities.

> How do the three elements of globalization, innovation, and sustainability impact your understanding of strategy?

> Use the Squeeze Theorem to show that lim x→0 (x2cos20πx) = 0. Illustrate by graphing the functions f(x) = -x2, g(x) = x2cos20πx, and h(x) = x2 on the same screen.

> a. Use a graph of f(x) = 3 + x - √3/x to estimate the value of limx → 0 f(x) to two decimal places. b. Use a table of values of f(x) to estimate the limit to four decimal places. c. Use the Limit Laws to find the exact value of the limit.

> a. Estimate the value of by graphing the function f(x) = x/(( 1 + 3x – 1). b. Make a table of values of f(x) for x close to 0 and guess the value of the limit. c. Use the Limit Laws to prove that your guess is correct. lim x-0

> Evaluate the limit, if it exists. 1 (x + h)? lim h0 h

> Evaluate the limit, if it exists. (x + h)³ – x³ lim h

> Evaluate the limit, if it exists. Vx? + 9 – 5 lim x + 4 4

> Evaluate the limit, if it exists. lim t/1 + t

> Evaluate the limit, if it exists. x? — 4х + 4 lim 2 x* - 3x? – 4

> Evaluate the limit, if it exists. 4 - VE lim 1-16 16x – x?

> Evaluate the limit, if it exists. lim 12 + t

> The point P(1, 0) lies on the curve y = sin(10π/x). a. If Q is the point (x, sin(10π/x), find the slope of the secant line PQ (correct to four decimal places) for x = 2, 1.5, 1.4, 1.3, 1.2, 1.1, 0.5, 0.6, 0.7, 0.8, and 0.9. Do the slopes appear to be

> Evaluate the limit, if it exists. VI +1 - VI - t lim

> Evaluate the limit, if it exists. (3 + h)`1 – 3-1 lim h

> Evaluate the limit, if it exists. 1 1 3 lim I-3 X - 3

> Evaluate the limit, if it exists. 4u + 1 – 3 lim 2 и — 2

> Evaluate the limit, if it exists. 9 +h - 3 lim 9 + h

> Evaluate the limit, if it exists. t* – 1 lim PI 13 - 1

> Evaluate the limit, if it exists. x + 2 -2 x' + 8 lim 3

> Evaluate the limit, if it exists. (2 + h)' – 8 lim h

> Evaluate the limit, if it exists. (-5 + h)? – 25 lim h

> Evaluate the limit, if it exists. 2x? + 3х + 1 lim x I x - 2x - 3

> The displacement (in centimeters) of a particle moving back and forth along a straight line is given by the equation of motion s = 2 sin πt + 3 cos π t, where t is measured in seconds. a. Find the average velocity during each time period: i. [1, 2] i

> Evaluate the limit, if it exists. t2 – 9 lim 3 212 + 7t + 3

> Evaluate the limit, if it exists. x² + 3x lim 4 x? - x - 12 – x –

> Evaluate the limit, if it exists. x' + 3x lim x3 x - x - 12

> Evaluate the limit, if it exists. x? — бх + 5 lim х — 5

> a. What is wrong with the following equation? x2 + x – 6/x - 2 = x + 3 b. In view of part (a), explain why the equation is correct. x? + x - 6 lim lim (x + 3) X - 2

> Evaluate the limit and justify each step by indicating the appropriate Limit Law(s). 2x2 + 1 lim →2 Зх — 2

> Evaluate the limit and justify each step by indicating the appropriate Limit Law(s). - 2 lim 2 13 – 3t + 5 12 – 2

> Evaluate the limit and justify each step by indicating the appropriate Limit Law(s). lim (1 + x)(2 – 6r? + x')

> Evaluate the limit and justify each step by indicating the appropriate Limit Law(s). lim yu4 + Зи +6 -2

> The table shows the position of a motorcyclist after accelerating from rest. a. Find the average velocity for each time period: i. [2, 4] ii. [3, 4] iii. [4, 5] iv. [4, 6] b. Use the graph of s as a function of t to estimate the instantan

> Evaluate the limit and justify each step by indicating the appropriate Limit Law(s). t4 - 2 lim "2 21? – 31 + 2

> Evaluate the limit and justify each step by indicating the appropriate Limit Law(s). lim (x* – 3x)(x² + 5x + 3) -1

> Evaluate the limit and justify each step by indicating the appropriate Limit Law(s). lim (5x* - 3x? + х — 6)

> The figure shows a fixed circle C1 with equation (x – 1)2 + y2 − 1 and a shrinking circle C2 with radius r and center the origin. P is the point (0, r), Q is the upper point of intersection of the two circles, and R is

> Is there a number a such that exists? If so, find the value of a and the value of the limit. 3x? Зx2 + ах + а +3 lim x→-2 х2 +x — 2

> Evaluate / 6 – x – 2/ 3 – x – 1.

> Explain what it means to say that In this situation is it possible that limx → 1 f(x) exists? Explain. lim f(x) = 3 and lim f(x) = 7 %3D

> Explain in your own words what is meant by the equation Is it possible for this statement to be true and yet f(2) = 3? Explain. lim f(x) = 5

> For the function f whose graph is shown, state the following. f. The equations of the vertical asymptotes. (a) lim f(x) (b) lim f(x) (c) lim f(x) X-7 X-3 (d) lim f(x) (e) lim f(x) X6+ y -7 6 3.

> For the function g whose graph is given, state the value of each quantity, if it exists. If it does not exist, explain why. (a) lim g(t) (b) lim g(t) (c) lim g(t) 0 (d) lim g(t) (e) lim g(t) 2+ (f) lim g(t) 2 (g) g(2) (h) lim g(t) 4 -2 4 2. 4,

> If a rock is thrown upward on the planet Mars with a velocity of 10 m/s, its height in meters t seconds later is given by y = 10t - 1.86t2. a. Find the average velocity over the given time intervals: i. [1, 2] ii. [1, 1.5] iii. [1, 1.1] iv. [1, 1.01

> For the function h whose graph is given, state the value of each quantity, if it exists. If it does not exist, explain why. (a) lim h(x) X-3 (b) X-3+ lim h(x) (c) lim_h(x) X-3 (d) h(-3) (e) lim h(x) (f) lim h(x) X0+ (g) lim h(x) (h) h(0) (i) lim h

> For the function f whose graph is given, state the value of each quantity, if it exists. If it does not exist, explain why. (a) lim f(x) (b) lim f(x) X3 (c) lim f(x) X3+ (d) lim f(x) (e) ƒ(3) y. 4 2 4 2.

> Use the given graph off to state the value of each quantity, if it exists. If it does not exist, explain why. (a) lim f(x) (b) lim f(x) (c) lim f(x) (d) f(2) (e) lim f(x) (f) f(4) 4 4 2. 2.

> Explain the meaning of each of the following. (a) lim f(x) = (b) lim f(x) X-3 X4+

> a. Use numerical and graphical evidence to guess the value of the limit b. How close to 1 does x have to be to ensure that the function in part (a) is within a distance 0.5 of its limit? x - 1 lim →1 Vx – 1

> For the function A whose graph is shown, state the following. e. The equations of the vertical asymptotes (a) lim A(x) (b) lim A(x) X2 X-3 (c) lim A(x) X2+ (d) lim A(x) -3 5 2.

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If limx → 5 f(x) = 2 and limx → 5 g(x) = 0, then limx → 5 [f(x)/g(x)] does not exist.

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. x? – 9 lim X-3 x - 3 lim (x + 3) X-

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. x2 – 9/x - 3 = x + 3

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. lim (x – 3) x – 3 lim l x? + 2x – 4 lim (x? + 2x – 4)

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. lim (x? + 6х — 7) х? + 6х — 7 lim х>і x? + 5х — 6 lim (x? + 5x – 6)

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. 2x lim X4 x - 4 2x 8 lim x→4x - 4 8 lim X4 X - 4 x - 4

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If | f | is continuous at a, so is f.

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f is continuous at a, so is | f |.

> In the theory of relativity, the mass of a particle with velocity v is where m0 is the mass of the particle at rest and c is the speed of light. What happens as v → c-? mo m = V1 - v²/c²

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. The equation x10 - 10x2 + 5 = 0 has a root in the interval (0, 2).

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. d2y/dx2=(dy/dx)2

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f’(r) exists, then limx → r f(x) = f(r).

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f is continuous at a, then f is differentiable at a.

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f(x) > 1 for all x and limx→0 f(x) exists, then limx→0 f(x) > 1.

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. Let f be a function such that limx→0 f(x) = 6. Then there exists a positive number δ such that if 0

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f is continuous on [-1, 1] and f(-1) = 4 and f(1) = 3, then there exists a number r such that |r

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f is continuous at 5 and f(5) = 2 and f(4) = 3, then limx → 2 f(4x2 – 11) = 2.

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f(1) > 0 and f(3) < 0, then there exists a number c between 1 and 3 such that f(c) = 0.

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If the line x = 1 is a vertical asymptote of y = f(x), then f is not defined at 1.

> Use a graph to estimate the equations of all the vertical asymptotes of the curve y = tan(2sinx) -π ≤ x ≤ π  Then find the exact equations of these asymptotes.

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f has domain (0, ∞) and has no horizontal asymptote, then lim x → ∞ f(x) = ∞ or limx → ∞ f(x) =

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. A function can have two different horizontal asymptotes.

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If limx → 0 f(x) = ∞ and limx → 0 g(x) = ∞, then limx → 0 [f(x) - g(x)] = 0.

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If p is a polynomial, then limx → b p(x) = p(b).

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If limx → 6 [f(x)g(x)] exists, then the limit must be f(6)g(6).

> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If limx → a f(x) exists but limx → a g(x) does not exist, then limx → a[f(x) + g(x)] does not exist