Question: Explain, using Theorems 4, 5, 7, and
Explain, using Theorems 4, 5, 7, and 9, why the function is continuous at every number in its domain. State the domain.
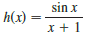
> Find the limit. limx→3+ ln (x2 – 9)
> Find the limit. limx→π cot x
> (a). From the graph of f, state the numbers at which f is discontinuous and explain why. (b). For each of the numbers stated in part (a), determine whether f is continuous from the right, or from the left, or neither.
> Find the limit. limx→2+ e3/ (2 – x)
> Find the limit. limx→-3- x + 2/ x + 3
> Find the limit. limx→1 2 - x/ (x – 1)2
> Use a graph to estimate all the vertical and horizontal asymptotes of the curve y = x3/x3 - 2x + 1
> Sketch the graph of an example of a function f that satisfies all of the given conditions.
> Write an equation that expresses the fact that a function is continuous at the number 4.
> A parking lot charges $3 for the first hour (or part of an hour) and $2 for each succeeding hour (or part), up to a daily maximum of $10. (a). Sketch a graph of the cost of parking at this lot as a function of the time parked there. (b). Discuss the disc
> Sketch the graph of a function that is continuous except for the stated discontinuity. Neither left nor right continuous at -2, continuous only from the left at 2
> Sketch the graph of a function that is continuous except for the stated discontinuity. Removable discontinuity at 3, jump discontinuity at 5
> Sketch the graph of a function that is continuous except for the stated discontinuity. Discontinuities at -1 and 4, but continuous from the left at -1 and from the right at 4
> Explain why the function is discontinuous at the given number a. Sketch the graph of the function.
> Guess the value of the limit (if it exists) by evaluating the function at the given numbers (correct to six decimal places).
> Guess the value of the limit (if it exists) by evaluating the function at the given numbers (correct to six decimal places).
> Guess the value of the limit (if it exists) by evaluating the function at the given numbers (correct to six decimal places).
> Sketch the graph of an example of a function f that satisfies all of the given conditions.
> Sketch the graph of an example of a function f that satisfies all of the given conditions.
> Sketch the graph of an example of a function f that satisfies all of the given conditions.
> Prove that cosine is a continuous function.
> Sketch the graph of a function that is continuous except for the stated discontinuity. Discontinuous, but continuous from the right, at 2
> If limx→1 f (x) – 8/x-1 = 10, find limx→1 f (x).
> If r is a rational function, use Exercise 43 to show that limv→a r (x) = r (a) for every number a in the domain of r. Exercise 43: If p is a polynomial, show that limv→a P (x) = P (a).
> If a rock is thrown upward on the planet Mars with a velocity of 10 m/s, its height (in meters) after seconds is given by H = 10t – 1.86t2. (a). Find the velocity of the rock after one second. (b). Find the velocity of the rock when t = a. (c). When will
> If p is a polynomial, show that limv→a P (x) = P (a).
> In the theory of relativity, the Lorentz contraction formula expresses the length L of an object as a function of its velocity v with respect to an observer, where l0 is the length of the object at rest and c is the speed of light. Find limv→c-L and inte
> Use the graph of the function f to state the value of each limit, if it exists. If it does not exist, explain why.
> From the graph of f, state the intervals on which is continuous.
> (a). If the symbol [[]] denotes the greatest integer function defined in Example 9, evaluate (b). If n is an integer, evaluate (c). For what values of does limx→a [x] exist?
> Suppose that a function f is continuous on [0, 1] except at 0.25 and that f (0) = 1 and f (1) = 3. Let N = 2. Sketch two possible graphs of f, one showing that f might not satisfy the conclusion of the Intermediate Value Theorem and one showing that f mi
> Let (a). Evaluate each of the following, if it exists. (b) Sketch the graph of g.
> Find the limit, if it exists. If the limit does not exist, explain why.
> Find the limit, if it exists. If the limit does not exist, explain why.
> The gravitational force exerted by the earth on a unit mass at a distance r from the center of the planet is where M is the mass of the earth, R is its radius, and G is the gravitational constant. Is F a continuous function of r?
> The graphs of f and t are given. Use them to evaluate each limit, if it exists. If the limit does not exist, explain why.
> Find the limit, if it exists. If the limit does not exist, explain why.
> Show that f is continuous on (-∞, ∞).
> Prove that limx→0 x4 cos 2/x = 0.
> Use continuity to evaluate the limit. limx→3 (x3 – 3x + 1)-3
> Evaluate the limit and justify each step by indicating the appropriate Limit Law(s).
> Use continuity to evaluate the limit. limx→π ex2-x
> Use continuity to evaluate the limit. limx→π sin (x + sin x)
> Use the Squeeze Theorem to show that limx→0 (x2 cos 20πx) = 0. Illustrate by graphing the functions f (x) = -x2, g (x) = x2 cos 20πx, and h (x) = x2 on the same screen.
> (a). Use a graph of f (x) = √3 + x - √3/x to estimate the value of limx→0 f (x) to two decimal places. (b). Use a table of values of f (x) to estimate the limit to four decimal places. (c). Use the Limit Laws to find the exact value of the limit.
> Locate the discontinuities of the function and illustrate by graphing. y = 1/1 + e1/x
> Shown are graphs of the position functions of two runners, A and B, who run a 100-m race and finish in a tie. (a). Describe and compare how the runners run the race. (b). At what time is the distance between the runners the greatest? (c). At what time
> Explain, using Theorems 4, 5, 7, and 9, why the function is continuous at every number in its domain. State the domain. F (x) = sin (cos (sin x))
> Explain, using Theorems 4, 5, 7, and 9, why the function is continuous at every number in its domain. State the domain. G (t) = ln (t4 – 1)
> Explain, using Theorems 4, 5, 7, and 9, why the function is continuous at every number in its domain. State the domain. L (t) = e-5t cos 2πt
> Explain, using Theorems 4, 5, 7, and 9, why the function is continuous at every number in its domain. State the domain.
> Evaluate the limit, if it exists. lim x → -4 1/4 + 1/x /4 + x
> Explain why the function is discontinuous at the given number a. Sketch the graph of the function.
> Explain why the function is discontinuous at the given number a. Sketch the graph of the function.
> Explain why the function is discontinuous at the given number a. Sketch the graph of the function.
> Evaluate the limit, if it exists. lim x → 0 (4 + h)2 – 16 / h
> (a). A particle starts by moving to the right along a horizontal line; the graph of its position function is shown. When is the particle moving to the right? Moving to the left? Standing still? (b). Draw a graph of the velocity function.
> Use the definition of continuity and the properties of limits to show that the function g (x) = 2 √3-x is continuous on the interval (-∞, 3].
> Use the definition of continuity and the properties of limits to show that the function is continuous at the given number a.
> Evaluate the limit, if it exists. lim x → 4 x2 - 4x / x2 – 3x - 4
> Evaluate the limit, if it exists. Lim x → 5 x2 - 6x + 5/ x - 5
> Sketch the graph of the function and use it to determine the values of for which limx→a f (x) exists.
> Evaluate the limit and justify each step by indicating the appropriate Limit Law(s).
> Evaluate the limit and justify each step by indicating the appropriate Limit Law(s).
> A patient receives a 150-mg injection of a drug every 4 hours. The graph shows the amount f (x) of the drug in the bloodstream after t hours. Find limt→12- f (t) and limt→12+ f (t) and explain the significance of these
> Evaluate the limit and justify each step by indicating the appropriate Limit Law(s).
> Use the graph of the function f to state the value of each limit, if it exists. If it does not exist, explain why.
> Explain why each function is continuous or discontinuous. (a). The temperature at a specific location as a function of time (b). The temperature at a specific time as a function of the distance due west from New York City (c). The altitude above sea leve
> Explain in your own words the meaning of each of the following.
> Apple Macs primarily use the __________ display connector type.
> The time it takes to redraw the entire screen is called the __________ .
> Two common projector technologies are LCD and ________________ .
> The __________ bus is the most common expansion slot for video cards.
> Using an aspect ratio of 16:10, the __________ refers to the number of horizontal pixels times the number of vertical pixels.
> DirectX is a(n) _____________ that translates instructions for the video device driver.
> The traditional D-subminiature connector on a video card is called a VGA connector or _________ .
> The size of the projected image at a specific distance from the screen is defined as the projector’s ___________ .
> To provide the optimal display for an LCD monitor, always set it to its ___________ .
> Virtual machines perform better on CPUs with ____________ .
> Before making a credit card purchase on the Internet, be sure the Web site uses the ______________ protocol (that replaced the older SSL protocol), which you can verify by checking for the __________ protocol in the address bar.
> Cloud computing companies provide ____________ that bills users for only what they use.
> A(n) ___________ is a virtual machine running on a hypervisor.
> A(n) __________ translates commands issued by software in order to run it on hardware it wasn’t designed to run on.
> You can use basic ____________ to create and run virtual machines on a local system.
> You can create a(n) _______ or ________ as a restore point for a virtual machine.
> John’s hypervisor enables all five of the virtual machines on his system to communicate with each other through the ____________ without going outside the host system.
> A program that runs multiple operating systems simultaneously is called a(n) __________ .
> A machine running a hypervisor is a(n) ____________ .
> A(n) _________ is a complete environment for a guest operating system to function as though that operating system was installed on its own computer.
> The ______________ applet provides a relative feel for how your computer stacks up against other systems using the Windows Experience Index.
> Many companies authenticate access to secure rooms using an ownership factor such as a(n)_______________ .
> To run a program written for Windows XP in a Windows 7 computer, use _________ if you encounter problems.
> In Windows Vista and Windows 7, you can use the _________ feature to recover previous versions of corrupted or deleted files.
> Use the ________ in Windows 8 to see an aggregation of event messages, warnings, maintenance messages, and quick access to security and maintenance tools.
> The___________ , accessed by pressing CTRL-SHIFT-ESC once, enables you to see all processes and services currently running or to close a process that has stopped working.
> To start Windows using only the most basic and essential drivers and services, use ________ .
> If Windows 7 fails but you have not logged on, you can select _________ to restore the computer to the way it was the last time a user logged on.
> Use the ___________ to check and replace any corrupted critical Windows files such as DLLs.
> Current versions of Windows include a set of repair tools known as the______________ .
> The _________ tool enables you to view and modify the BCD store.

