Question: Express each proposition as an English sentence
Express each proposition as an English sentence and determine whether it is true or false, where r and s are the propositions
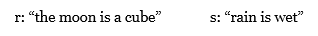
r ( s
> For U = {7, 8, 9, 10, 11} and A = {7, 11}, find A′.
> write the resulting set using the listing method. {x | x is a month starting with M}
> write the resulting set using the listing method. {x | x4 = 16}
> Use the given interest rate i per compounding period to find r, the annual rate. 0.012% per day
> write the resulting set using the listing method. {x | x2 = 36}
> write the resulting set using the listing method. {-3, -1,} ∪ {1, 3}
> write the resulting set using the listing method. {-3, -1} ∩ {1, 3}
> write the resulting set using the listing method. {1, 2, 4} ∩{4, 8, 16}
> write the resulting set using the listing method. {1, 2, 4} ∪ {4, 8, 16}
> Indicate true (T) or false (F). ∅ ⊂ {1, 2, 3}
> Indicate true (T) or false (F). {0, 6} = {6}
> Explain why the product of any two odd integers is odd
> Refer to the footnote for the definitions of divisor, multiple, prime, even, and odd. List the primes between 10 and 20.
> Refer to the footnote for the definitions of divisor, multiple, prime, even, and odd. List the positive multiples of 9 that are less than 50
> Use formula (1) for simple interest to find each of the indicated quantities. I = $96; P = $3,200; r = 4%; t = ?
> Refer to the footnote for the definitions of divisor, multiple, prime, even, and odd. List the positive integers that are divisors of 24.
> Can a conditional proposition be false if its converse is true? Explain.
> If the conditional proposition p is a contradiction, is ¬p a contingency, a tautology, or a contradiction? Explain.
> Let p be the proposition “every politician is honest.” Explain why the statement “every politician is dishonest” is not equivalent to ¬p. Express ¬p as an English sentence without using the word not.
> verify each equivalence using formulas from Table 2. ¬(¬p → ¬q) ( q ( ¬p
> verify each equivalence using formulas from Table 2. ¬p → q ( p ( q
> construct a truth table to verify each equivalence. p → (p ( q) ( p → q
> construct a truth table to verify each equivalence. p ( (p → q) ( p ( q
> Construct a truth table to verify each equivalence. q → (¬p ( q) ( ¬(p ( q)
> Construct a truth table to verify each implication. (p ( ¬p) ( q
> Use the given interest rate i per compounding period to find r, the annual rate. 1.57% per quarter
> Evaluate the expression. If the answer is not an integer, round to four decimal places.
> construct a truth table to verify each implication. p ( q ( p → q
> construct a truth table to verify each implication. ¬p ( p → q
> Construct a truth table for the proposition and determine whether the proposition is a contingency, tautology, or contradiction. (p →¬q) ( (p ( q)
> Construct a truth table for the proposition and determine whether the proposition is a contingency, tautology, or contradiction. q → (p (¬ q)
> Construct a truth table for the proposition and determine whether the proposition is a contingency, tautology, or contradiction. ¬ p → (p ( q)
> Construct a truth table for the proposition and determine whether the proposition is a contingency, tautology, or contradiction. (p → q) → ¬q
> Construct a truth table for the proposition and determine whether the proposition is a contingency, tautology, or contradiction. p → (p ( q)
> Construct a truth table for the proposition and determine whether the proposition is a contingency, tautology, or contradiction. p ( (p → q)
> Construct a truth table for the proposition and determine whether the proposition is a contingency, tautology, or contradiction. q ( (p ( q)
> Construct a truth table for the proposition and determine whether the proposition is a contingency, tautology, or contradiction. p → ¬q
> Use formula (1) for simple interest to find each of the indicated quantities. I = $28; P = $700; t = 13 weeks; r = ?
> Construct a truth table for the proposition and determine whether the proposition is a contingency, tautology, or contradiction. p ( ¬ q
> State the converse and the contrapositive of the given proposition. If n is an integer that is a multiple of 6, then n is an integer that is a multiple of 2 and a multiple of 3.
> State the converse and the contrapositive of the given proposition. If g1x2 is a quadratic function, then g1x2 is a function that is neither increasing nor decreasing.
> State the converse and the contrapositive of the given proposition. If triangle ABC is isosceles, then the base angles of triangle ABC are congruent.
> Describe each proposition as a negation, disjunction, conjunction, or conditional, and determine whether the proposition is true or false. If 4 is even, then 4 is prime
> Describe each proposition as a negation, disjunction, conjunction, or conditional, and determine whether the proposition is true or false. 9 is even or 9 is prime
> Describe each proposition as a negation, disjunction, conjunction, or conditional, and determine whether the proposition is true or false. -3 is not greater than 0
> Describe each proposition as a negation, disjunction, conjunction, or conditional, and determine whether the proposition is true or false. -3 < 0 and -3 > 0
> Express each proposition as an English sentence and determine whether it is true or false, where r and s are the propositions The converse of s ( r
> Express each proposition as an English sentence and determine whether it is true or false, where r and s are the propositions ¬ r
> Use the given annual interest rate r and the compounding period to find i, the interest rate per compounding period. 10.95% compounded daily
> Express each proposition as an English sentence and determine whether it is true or false, where p and q are the propositions. p: “91 is prime” q: “91 is odd” The contrapositive of p → q
> Express each proposition as an English sentence and determine whether it is true or false, where p and q are the propositions. p: “91 is prime” q: “91 is odd” p → q
> Express each proposition as an English sentence and determine whether it is true or false, where p and q are the propositions. p: “91 is prime” q: “91 is odd” p v q
> (A) Introduce slack, surplus, and artificial variables and form the modified problem. (B) Write the preliminary simplex tableau for the modified problem and find the initial simplex tableau. (C) Find the optimal solution of the modified problem by appl
> (A) Introduce slack, surplus, and artificial variables and form the modified problem. (B) Write the preliminary simplex tableau for the modified problem and find the initial simplex tableau. (C) Find the optimal solution of the modified problem by appl
> (A) Introduce slack, surplus, and artificial variables and form the modified problem. (B) Write the preliminary simplex tableau for the modified problem and find the initial simplex tableau. (C) Find the optimal solution of the modified problem by appl
> (A) Introduce slack, surplus, and artificial variables and form the modified problem. (B) Write the preliminary simplex tableau for the modified problem and find the initial simplex tableau. (C) Find the optimal solution of the modified problem by appl
> Construct a mathematical model in the form of a linear programming problem. Do not solve. A farmer grows three crops: corn, oats, and soybeans. He mixes them to feed his cows and pigs. At least 40% of the feed mix for the cows must be corn. The feed mix
> Construct a mathematical model in the form of a linear programming problem. Do not solve. Refer to Problem 43. Suppose the investor decides that she would like to minimize the total risk factor, as long as her return does not fall below 9%. What percenta
> Use formula (1) for simple interest to find each of the indicated quantities. I = $15; r = 8%; t = 3 quarters; P = ?
> Construct a mathematical model in the form of a linear programming problem. Do not solve. A company makes two brands of trail mix, regular and deluxe, by mixing dried fruits, nuts, and cereal. The recipes for the mixes are given in the table. The compan
> Construct a mathematical model in the form of a linear programming problem. Do not solve. A savings and loan company has $3 million to lend. The types of loans and annual returns offered are given in the table. State laws require that at least 50% of th
> Construct a mathematical model in the form of a linear programming problem. Then solve the problem using the big M method. Discuss the effect on the solution to Problem 37 if the limit on phosphoric acid is increased to 1,000 pounds. Data from Problem 3
> Construct a mathematical model in the form of a linear programming problem. Then solve the problem using the big M method. Discuss the effect on the solution to Problem 35 if the cost of brand C liquid diet food increases to $1.50 per bottle. Data from
> Construct a mathematical model in the form of a linear programming problem. Then solve the problem using the big M method. Discuss the effect on the solution to Problem 33 if the Tribune will not accept more than 4 ads from the company Data from Problem
> Solve the Problem by the methods presented in Sections 6.2 and 6.3.
> Solve the Problem by the methods presented in Sections 6.2 and 6.3.
> Solve the Problem by the methods presented in Sections 6.2 and 6.3.
> Solve the Problem by the methods presented in Sections 6.2 and 6.3.
> Solve Problems 6 and 8 by graphing (the geometric method)
> Use the given annual interest rate r and the compounding period to find i, the interest rate per compounding period. 5.44% compounded quarterly
> Use the big M method to solve the Problem.
> Use the big M method to solve the Problem.
> Use the big M method to solve the Problem.
> Use the big M method to solve the Problem.
> Use the big M method to solve the Problem.
> Use the big M method to solve the Problem.
> Use the big M method to solve the Problem.
> Find the transpose of each matrix.
> Find the transpose of each matrix.
> Find the transpose of each matrix.
> Use formula (1) for simple interest to find each of the indicated quantities. P = $950; r = 9%; t = 1 year; I = ?
> Repeat Problem 57 if the weekly cost of busing a student from North Division to Washington is $7 and all other data remain the same. Data From Problem 57: A metropolitan school district has two overcrowded high schools and two underenrolled high schools
> A farmer can buy three types of plant food: mix A, mix B, and mix C. Each cubic yard of mix A contains 20 pounds of phosphoric acid, 10 pounds of nitrogen, and 10 pounds of potash. Each cubic yard of mix B contains 10 pounds of phosphoric acid, 10 pounds
> Repeat Problem 50 if it costs $800 per hour to operate the West Summit mine and $200 per hour to operate the North Ridge mine and all other data remain the same. Data from Problem 50: A mining company operates two mines, each producing three grades of o
> Repeat Problem 50 if it costs $300 per hour to operate the West Summit mine and $700 per hour to operate the North Ridge mine and all other data remain the same. Data from Problem 50: A mining company operates two mines, each producing three grades of o
> A mining company operates two mines, each producing three grades of ore. The West Summit mine can produce 2 tons of low-grade ore, 3 tons of medium-grade ore, and 1 ton of high-grade ore in one hour of operation. The North Ridge mine can produce 2 tons o
> Solve the linear programming problems by applying the simplex method to the dual problem. Repeat Problem 47 with C = 4x1 + 7x2 + 5x3 + 6x4 Data from Problem 47:
> Solve the linear programming problems by applying the simplex method to the dual problem.
> (A) Form an equivalent minimization problem with Ú problem constraints (multiply inequalities by -1 if necessary), (B) Form the dual of the equivalent problem. (C) Is the dual problem a standard maximization problem in standard form? Expla
> (A) Form the dual problem. (B) Is the dual problem a standard maximization problem in standard form? Explain
> If you want to solve a minimization problem by applying the geometric method to the original problem, how many variables and problem constraints must be in the original problem?
> Use the given annual interest rate r and the compounding period to find i, the interest rate per compounding period. 2.94% compounded semiannually
> A minimization problem has 3 variables and 5 problem constraints. How many variables and problem constraints are in the dual problem?
> Solve the linear programming problems by applying the simplex method to the dual problem.
> Solve the linear programming problems by applying the simplex method to the dual problem.
> Solve the linear programming problems by applying the simplex method to the dual problem.
> Solve the linear programming problems by applying the simplex method to the dual problem.
> Solve the linear programming problems by applying the simplex method to the dual problem.
> Solve the linear programming problems by applying the simplex method to the dual problem.
> Solve the linear programming problems by applying the simplex method to the dual problem.

