Question: Find a power series representation for the
Find a power series representation for the function and determine the interval of convergence.
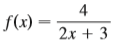
Transcribed Image Text:
f(x) 2x + 3 4-
> Find the values of p for which the integral converges and evaluate the integral for those values of p. dx Jo
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. sin'x
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. 2. sec?r xVx
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. arctan x dx Jo 2 + e*
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. x + 1 dx /x4 — х
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. 1 + sin?x dx
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. dx J. x +1
> Find a power series representation for the function and determine the interval of convergence. x + a S(x). a > 0 x² + a²'
> (a) If g(x) = (sin2x)/x2 use your calculator or computer to make a table of approximate values of / for t = 2, 5, 10, 100, 1000, and 10,000. Does it appear that / is convergent? (b) Use the Comparison Theorem with f(x) = 1/x2 to show that / is convergent
> Sketch the region and find its area (if the area is finite). S = {(x, y) | –2 <x< 0, 0<y< 1//x + 2}
> Sketch the region and find its area (if the area is finite). S = {(x, y) | 0 < x < m/2, 0 < y < sec²x}
> Sketch the region and find its area (if the area is finite). s = {(x, y) | x > 0, 0 < y< xe *}
> Sketch the region and find its area (if the area is finite). s = {(x, y) | x > 1, 0 < y< 1/(x³ + x)}
> Sketch the region and find its area (if the area is finite). S = {(x, y) | x < 0, 0 < y< e*}
> Sketch the region and find its area (if the area is finite). S = {(x, y) | x > 1, 0 < y<e}
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1/1 e dx
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. ,1/x x³
> Find a power series representation for the function and determine the interval of convergence. x - 1 x + 2 S(x)
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. cos 0 do (a/2 sin 0
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. I'r In r dr
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. dx x? — х — 2
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. *w/2 ´tan?0 d0 Jo
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. /
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 6. dx Jo I - xA
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. (x + 1)?
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. '14 dx Vx + 2
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent.
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. e Jo dy
> Find a power series representation for the function and determine the interval of convergence. S(x) 2x? + 1
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1 Je x(In x)? dx 2
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. zp z4 + 4
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. In x - dx .2
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. ye » dy Зу 12
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. L. zeª dz
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. dv 12 v² + 2v – 3
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1 dx x² + x
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. sine ecoso de Jo
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. L xe * dx
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. L( – 3y°) dy
> Find a power series representation for the function and determine the interval of convergence. x? S(x) x* + 16
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1 dx ах V1 + x
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1 dx (x – 2)½ J3
> (a) Graph the functions f(x) = 1/x1.1 and t(x) = 1/x0.9 in the viewing rectangles [0, 10] by [0, 1] and [0, 100] by [0, 1]. (b) Find the areas under the graphs of f and t from x = 1 to x = t and evaluate for t = 10, 100, 104, 106, 1010, and 1020. (c) Fin
> Find the area under the curve y = 1/x3 from x = 1 to x = t and evaluate it for t = 10, 100, and 1000. Then find the total area under this curve for x > 1.
> Which of the following integrals are improper? Why? (a) " tan x dx (b) " tan x dx dx (c) ix? (d) fe*dx 2 – x – 2
> Explain why each of the following integrals is improper. (a) f -dx 1 1 - dx Jo 1 + x³ (b) X - (c) x'e * dx cot x dx
> The curves with equations xn + yn = 1, n = 4, 6, 8, . . . , are called fat circles. Graph the curves with n = 2, 4, 6, 8, and 10 to see why. Set up an integral for the length L2k of the fat circle with n = 2k. Without attempting to evaluate this integra
> Find the length of the curve yーfp- 13 – 1 dt 1<x< 4
> (a) The figure shows a telephone wire hanging between two poles at x 2b and x b. It takes the shape of a catenary with equation y c + a cosh (x/a). Find the length of the wire. (b) Suppose two telephone poles are 50 ft apart and the length of
> The Gateway Arch in St. Louis (see the photo on page 543) was constructed using the equation for the central curve of the arch, where x and y are measured in meters and |x| y = 211.49 – 20.96 cosh 0.03291765x
> A hawk flying at 15 m/s at an altitude of 180 m accidentally drops its prey. The parabolic trajectory of the falling prey is described by the equation until it hits the ground, where y is its height above the ground and x is the horizontal distance trave
> A steady wind blows a kite due west. The kite’s height above ground from horizontal position x = 0 to x = 80 ft is given by / Find the distance traveled by the kite.
> The arc length function for a curve y = f x), where f is an increasing function, is / (a) If f has y intercept 2, find an equation for f. (b) What point on the graph off is 3 units along the curve from the y intercept? State your answer rounded to 3 de
> Find the arc length function for the curve y = sin 'x + V1 – x² with starting point (0, 1)
> (a) Find the arc length function for the curve y = In(sin x), (b) Graph both the curve and its arc length function on the same screen. 0<x< T, with starting point (7/2, 0)
> Find the arc length function for the curve y = 2x3/2 with starting point P0(1, 2).
> (a) Sketch the curve y3 = x2. (b) Use Formulas 3 and 4 to set up two integrals for the arc length from (0, 0) to (1, 1). Observe that one of these is an improper integral and evaluate both of them. (c) Find the length of the arc of this curve from (21, 1
> Sketch the curve with equation x2/3 + y2/3 = 1 and use symmetry to find its length.
> Find a power series representation for the function and determine the interval of convergence. 2 S(x) 3 — х
> Use either a computer algebra system or a table of integrals to find the exact length of the arc of the curve y = x4/3 that lies between the points (0, 0) and (1, 1). If your CAS has trouble evaluating the integral, make a substitution that changes the i
> Use either a computer algebra system or a table of integrals to find the exact length of the arc of the curve y = ex that lies between the points (0, 1) and (2, e2).
> Repeat Exercise 29 for the curve Data from Exercise 29: (a) Graph the curve / (b) Compute the lengths of inscribed polygons with n = 1, 2, and 4 sides. (Divide the interval into equal sub intervals.) Illustrate by sketching these polygons. (c) Set up a
> Use Simpson’s Rule with n = 10 to estimate the arc length of the curve. Compare your answer with the value of the integral produced by a calculator. y = e *, 0<x< 2
> Use Simpson’s Rule with n = 10 to estimate the arc length of the curve. Compare your answer with the value of the integral produced by a calculator. y = In(1 + x³), 0 <x< 5
> Use Simpson’s Rule with n = 10 to estimate the arc length of the curve. Compare your answer with the value of the integral produced by a calculator. y = Vx, 1<x< 6
> Use Simpson’s Rule with n = 10 to estimate the arc length of the curve. Compare your answer with the value of the integral produced by a calculator. y = x sin x, 0 <x< 27
> Graph the curve and visually estimate its length. Then use your calculator to find the length correct to four decimal places. y = x + cos x, 0<x<T/2
> Graph the curve and visually estimate its length. Then use your calculator to find the length correct to four decimal places. y = x² + x', 1 <x<2
> Find a power series representation for the function and determine the interval of convergence. 5 S(x) 1 – 4x?
> (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate the accuracy of the approximation / when x lies in the given interval. (c) Check your result in part (b) by graphing / S
> Find the length of the arc of the curve from point P to point Q. х? — (у — 4), Р(1, 5), Q(8, 8)
> Find the length of the arc of the curve from point P to point Q. y = }x', P(-1, ), e(1,4)
> Find the exact length of the curve. y = 1- e, 0<x<2
> Find the exact length of the curve. y = In(1 – x'), 0 <x<}
> Find the exact length of the curve. у — Vx (x) y = — х2 + sin
> Find the exact length of the curve. y = x? - } In x, 1<x<2
> Find the exact length of the curve. y = 3 + cosh 2.x, 0<x<1
> Find the exact length of the curve. у — In(sec x), 0<x< п/4 y
> Find the exact length of the curve. y = In(cos x), 0 <x</3 %3|
> Find the exact length of the curve. 3 Vy (у — 3), 1<y<9
> Find a power series representation for the function and determine the interval of convergence. 1 1+ x S(x)
> Find the exact length of the curve. 1 1<y<2 8 4y² +
> Find the exact length of the curve. 1<x<2 y = 3 4x +
> Find the exact length of the curve. 36y? = (x² – 4), 2<x<3, y > 0 %3D
> Find the exact length of the curve. y = 1 + 6x2, 0<x<1 3/2
> Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. y? = In x, -1 < y< 1
> Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. x= Vy - y, 1< y< 4 X =
> Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. y = xe, 0<I<2
> Use the arc length formula to find the length of the curve / Check your answer by noting that the curve is part of a circle.
> Use the arc length formula (3) to find the length of the curve y = 2x - 5, 21 < x < 3. Check your answer by noting that the curve is a line segment and calculating its length by the distance formula.
> Formula 4 is valid only when f(x) > 0. Show that when f(x) is not necessarily positive, the formula for surface area becomes s = [" 27| f(x)|/T +[S(x)F dx
> Let L be the length of the curve y = f(x), a < x < b, where f is positive and has a continuous derivative. Let Sf be the surface area generated by rotating the curve about the x axis. If c is a positive constant, define t(x) = f(x) 1 c and let St be the
> Show that if we rotate the curve y = ex/2 + ex/2 about the x axis, the area of the resulting surface is the same value as the enclosed volume for any interval a < x < b.
> Find the area of the surface obtained by rotating the circle x2 + y2 = r2 about the line y = r.
> Use the result of Exercise 33 to set up an integral to find the area of the surface generated by rotating the curve / 0 < x < 4, about the line y = 4. Then use a CAS to evaluate the integral. Data from Exercise 33: If the curve y = f(x), a < x < b, is
> If the curve y = f(x), a < x < b, is rotated about the horizontal line y = c, where f(x) < c, find a formula for the area of the resulting surface.
> Find the surface area of the torus in Exercise 6.2.63. Data from Exercise 6.2.63: (a) Set up an integral for the volume of a solid torus (the donut-shaped solid shown in the figure) with radii r and R. (b) By interpreting the integral as an area, find
> A group of engineers is building a parabolic satellite dish whose shape will be formed by rotating the curve y = ax2 about the y axis. If the dish is to have a 10ft diameter and a maximum depth of 2 ft, find the value of a and the surface area of the d
> (a) If a > 0, find the area of the surface generated by rotating the loop of the curve 3ay2 = x (a - x)2 about the x axis. (b) Find the surface area if the loop is rotated about the y axis.
> If the infinite curve y = ex, x > 0, is rotated about the x axis, find the area of the resulting surface.

