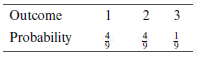
Question: Find E(X ), Var(X ), and the
Find E(X ), Var(X ), and the standard deviation of X, where X is the random variable whose probability table is given in Table 5.
Table 5:
> Find the value of k that makes the given function a probability density function on the specified interval. f (x) = k, 5 ≤ x ≤ 20
> Find the value of k that makes the given function a probability density function on the specified interval. f (x) = kx2, 0 ≤ x ≤ 2
> Find the value of k that makes the given function a probability density function on the specified interval. f (x) = kx, 1 ≤ x ≤ 3
> The annual incomes of the households in a certain community range between 5 and 25 thousand dollars. Let X represent the annual income (in thousands of dollars) of a household chosen at random in this community, and suppose that the probability density f
> Verify that each of the following functions is a probability density function. f (x) = 3/2 x – ¾ x2, 0 ≤ x ≤ 2
> Verify that each of the following functions is a probability density function. f (x) = 5x4, 0 ≤ x ≤ 1
> Verify that each of the following functions is a probability density function. f (x) = 8/9 x, 0 ≤ x ≤ 3/2
> Verify that each of the following functions is a probability density function. f (x) = ¼, 1 ≤ x ≤ 5
> Verify that each of the following functions is a probability density function. f (x) = 2(x - 1), 1 ≤ x ≤ 2
> Let X be a continuous random variable with the density function f (x) = 2(x + 1)-3, x ≥ 0. (a) Verify that f (x) is a probability density function for x ≥ 0. (b) Find the cumulative distribution function for X. (c) Compute Pr (1 ≤ X ≤ 2) and Pr (3 ≤ X ).
> Let X be a continuous random variable with values between A = 1 and B = ∞, and with the density function f (x) = 4x-5. (a) Verify that f (x) is a probability density function for x ≥ 1. (b) Find the corresponding cumulative distribution function F (x). (
> A random variable X has a cumulative distribution function F (x) = (x - 1)2 on 1 ≤ x ≤ 2. Find b such that Pr (X ≤ b) = ¼.
> A random variable X has a cumulative distribution function F (x) = 1/4 x2 on 0 ≤ x ≤ 2. Find b such that Pr (X ≤ b) = .09.
> A random variable X has a density function f (x) = 2/3 x on 1 ≤ x ≤ 2. Find a such that Pr (a ≤ X ) = 13.
> A random variable X has a cumulative distribution function F (x) = (x2 - 9)>16 on 3 ≤ x ≤ 5. (a) Find the density function for X. (b) Find a such that Pr (a ≤ X ) = ¼.
> A random variable X has a density function f (x) = 1/3, 0 ≤ x ≤ 3. Find b such that Pr (0 ≤ X ≤ b) = .6.
> In a certain cell population, cells divide every 10 days, and the age of a cell selected at random is a random variable X with the density function f (x) = 2ke-kx, 0 ≤ x ≤ 10, k = (ln 2)/10. Upon examination of a slide, 10% of the cells are found to be u
> In a certain cell population, cells divide every 10 days, and the age of a cell selected at random is a random variable X with the density function f (x) = 2ke-kx, 0 ≤ x ≤ 10, k = (ln 2)/10. Find the probability that a cell is at most 5 days old.
> An experiment consists of selecting a point at random from the region inside the triangle in Fig. 10(b). Let X be the sum of the coordinates of the point. Find the corresponding density function of X. Figure 10(b):
> An experiment consists of selecting a point at random from the region inside the triangle in Fig. 10(b). Let X be the sum of the coordinates of the point. Show that the cumulative distribution function of X is F (x) = x2/4, 0 ≤ x &aci
> An experiment consists of selecting a point at random from the region inside the square in Fig. 10(a). Let X be the maximum of the coordinates of the point. Find the corresponding density function of X. Figure 10(a):
> An experiment consists of selecting a point at random from the region inside the square in Fig. 10(a). Let X be the maximum of the coordinates of the point. Show that the cumulative distribution function of X is F (x) = x2/4, 0 ≤ x &a
> The density function for a continuous random variable X on the interval 1 ≤ x ≤ 4 is f (x) = 4/9 x – 1/9 x2. (a) Use f (x) to compute Pr (3 ≤ X ≤ 4). (b) Find the corresponding cumulative distribution function F (x). (c) Use F (x) to compute Pr (3 ≤ X ≤
> The time (in minutes) required to complete a certain subassembly is a random variable X with the density function f (x) = 1/21 x2, 1 ≤ x ≤ 4. (a) Use f (x) to compute Pr (2 ≤ X ≤ 3). (b) Find the corresponding cumulative distribution function F (x). (c)
> Compute the cumulative distribution function corresponding to the density function f (x) = ½ (3 - x), 1 ≤ x ≤ 3.
> A random variable X has a uniform density function f (x) = 15 on 20 ≤ x ≤ 25. (a) Find E (X ) and Var (X ). (b) Find b such that Pr (X ≤ b) = .3.
> Compute the cumulative distribution function corresponding to the density function f (x) = 1/5 , 2 ≤ x ≤ 7.
> The cumulative distribution function for a random variable X on the interval 1 ≤ x ≤ 2 is F (x) = 4/3 – 4/(3x2). Find the corresponding density function.
> The cumulative distribution function for a random variable X on the interval 1 ≤ x ≤ 5 is F (x) = ½ √(x – 1). (See Fig. 9.) Find the corresponding density function.
> At a certain supermarket, the amount of wait time at the express lane is a random variable with density function f (x) = 11/[10(x + 1)2], 0 ≤ x ≤ 10. (See Fig. 8.) Find the probability of having to wait less than 4
> Suppose that the lifetime X (in hours) of a certain type of flashlight battery is a random variable on the interval 30 ≤ x ≤ 50 with density function f (x) = 1/20, 30 ≤ x ≤ 50. Find the probability that a battery selected at random will last at least 35
> Find Pr (1 ≤ X ) when X is a random variable whose density function is given in Exercise 4. Exercise 4: f (x) = 8/9 x, 0 ≤ x ≤ 3/2
> Find Pr (X ≤ 3) when X is a random variable whose density function is given in Exercise 3. Exercise 3: f (x) = ¼, 1 ≤ x ≤ 5
> Find Pr (1.5 ≤ X ≤ 1.7) when X is a random variable whose density function is given in Exercise 2. Exercise 2: f (x) = 2(x - 1), 1 ≤ x ≤ 2
> Find Pr(1 ≤ X ≤ 2) when X is a random variable whose density function is given in Exercise 1. Exercise 1: f (x) = 1/18 x, 0 ≤ x ≤ 6
> The density function of a continuous random variable X is f (x) = 3x2, 0 ≤ x ≤ 1. Sketch the graph of f (x) and shade in the areas corresponding to (a) Pr (X ≤ .3); (b) Pr (.5 ≤ X ≤ .7); (c) Pr (.8 ≤ X ).
> A service contract on a computer costs $100 per year. The contract covers all necessary maintenance and repairs on the computer. Suppose that the actual cost to the manufacturer for providing this service is a random variable X (measured in hundreds of d
> The density function of a continuous random variable X is f (x) = 1/8 x, 0 ≤ x ≤ 4. Sketch the graph of f (x) and shade in the areas corresponding to (a) Pr (X ≤ 1); (b) Pr (2 ≤ X ≤ 2.5); (c) Pr (3.5 ≤ X ).
> Find the value of k that makes the given function a probability density function on the specified interval. f (x) = k(3x - x2), 0 ≤ x ≤ 3
> Find the value of k that makes the given function a probability density function on the specified interval. f (x) = kx2(1 - x), 0 ≤ x ≤ 1
> Suppose that the weather forecast in Exercise 9 indicates a 10% chance that cold weather will reduce the citrus grower’s profit from $100,000 to $85,000 and a 10% chance that cold weather will reduce the profit to $75,000. Should the grower spend $5000 t
> A citrus grower anticipates a profit of $100,000 this year if the nightly temperatures remain mild. Unfortunately, the weather forecast indicates a 25% chance that the temperatures will drop below freezing during the next week. Such freezing weather will
> Consider a circle with circumference 1. An arrow (or spinner) is attached at the center so that, when flicked, it spins freely. Upon stopping, it points to a particular point on the circumference of the circle. Determine the likelihood that the point is
> Consider a circle with radius 1. (a) What percentage of the points lies within ½ unit of the center? (b) Let c be a constant with 0 < c < 1. What percentage of the points lies within c unit of the center?
> The number of phone calls coming into a telephone switchboard during each minute was recorded during an entire hour. During 30 of the 1-minute intervals there were no calls, during 20 intervals there was one call, and during 10 intervals there were two c
> The number of accidents per week at a busy intersection was recorded for a year. There were 11 weeks with no accidents, 26 weeks with one accident, 13 weeks with two accidents, and 2 weeks with three accidents. A week is to be selected at random and the
> Compute the variances of the two random variables whose probability tables are given in Table 7. Relate the sizes of the variances to the spread of the values of the random variables. Table 7:
> A certain gas station sells X thousand gallons of gas each week. Suppose that the cumulative distribution function for X is F (x) = 1 – ¼ (2 - x)2, 0 ≤ x ≤ 2. (a) If the tank contains 1.6 thousand gallons at the beginning of the week, find the probabilit
> Compute the variances of the three random variables whose probability tables are given in Table 6. Relate the sizes of the variances to the spread of the values of the random variable. Table 6:
> Table 4 is the probability table for a random variable X. Find E(X ), Var(X ), and the standard deviation of X. Table 4:
> For any positive integer n, the function fn(x) = cn x(n-2)/2 e-x/2, x ≥ 0, where cn is an appropriate constant, is called the chi-square density function with n degrees of freedom. Find c2 and c4 such that f2 (x) and f4 (x) are probability density functi
> For any positive constants k and A, verify that the function f (x) = kAk/xk+1, x ≥ A, is a density function. The associated cumulative distribution function F (x) is called a Pareto distribution. Compute F (x).
> For any number A, verify that f (x) = eA-x, x ≥ A, is a density function. Compute the associated cumulative distribution for X.
> Let X be a continuous random variable on 3 ≤ x ≤ 4, with the density function f (x) = 2(x - 3). (a) Calculate Pr (3.2 ≤ X ) and Pr (3 ≤ X ). (b) Find E(X ) and Var(X ).
> Let X be a continuous random variable on 0 ≤ x ≤ 2, with the density function f (x) = 3/8 x2. (a) Calculate Pr (X ≤ 1) and Pr (1 ≤ X ≤ 1.5). (b) Find E(X ) and Var (X ).
> A pair of dice is rolled until a 7 or an 11 appears, and the number of rolls preceding the final roll is observed. The probability of rolling 7 or 11 is 2/9. What is the probability that at least three consecutive rolls precede the final roll?
> A pair of dice is rolled until a 7 or an 11 appears, and the number of rolls preceding the final roll is observed. The probability of rolling 7 or 11 is 2/9. Determine the average number of consecutive rolls preceding the final roll.
> If the laboratory in Exercise 7 uses batches of 5 instead of 10 samples, the probability of a negative test on the mixture of 5 samples is (.95)5 = .774. Thus, Table 2 gives the probabilities for the number X of tests required. (a) Find E(X ). (b) If the
> A pair of dice is rolled until a 7 or an 11 appears, and the number of rolls preceding the final roll is observed. The probability of rolling 7 or 11 is 2/9. Determine the formula for pn, the probability of exactly n consecutive rolls preceding the final
> A small volume of blood is selected and examined under a microscope, and the number of white blood cells is counted. Suppose that for healthy people the number of white blood cells in such a specimen is Poisson distributed with λ = 4. What is the average
> A small volume of blood is selected and examined under a microscope, and the number of white blood cells is counted. Suppose that for healthy people the number of white blood cells in such a specimen is Poisson distributed with λ = 4. What is the probabi
> A small volume of blood is selected and examined under a microscope, and the number of white blood cells is counted. Suppose that for healthy people the number of white blood cells in such a specimen is Poisson distributed with λ = 4. What is the probabi
> Do the same as in Exercise 29 with a normal random variable. Exercise 29: The Chebyshev inequality says that for any random variable X with expected value m and standard deviation σ, Pr (µ - nσ ≤ X ≤ µ + nσ) ≥ 1 -1/n2. (a) Take n = 2. Apply the Chebyshe
> The Chebyshev inequality says that for any random variable X with expected value m and standard deviation σ, Pr (µ - nσ ≤ X ≤ µ + nσ) ≥ 1 -1/n2. (a) Take n = 2. Apply the Chebyshev inequality to an exponential random variable. (b) By integrating, find th
> (a) Show that about 95% of the area under the standard normal curve lies between -2 and 2. (b) Let X be a normal random variable with expected value µ and variance σ2. Compute Pr (µ - 2σ ≤ X ≤ µ + 2σ).
> It is useful in some applications to know that about 68% of the area under the standard normal curve lies between -1 and 1. (a) Verify this statement. (b) Let X be a normal random variable with expected value µ and variance σ2. Compute Pr (µ - σ ≤ X ≤ µ
> Scores on an entrance exam Scores on a school’s entrance exam are normally distributed, with µ = 500 and σ = 100. If the school wishes to admit only the students in the top 40%, what should be the cutoff grade?
> Let Z be a standard normal random variable. Find the number a such that Pr (a ≤ Z ) = .40.
> A medical laboratory tests many blood samples for a certain disease that occurs in about 5% of the samples. The lab collects samples from 10 persons and mixes together some blood from each sample. If a test on the mixture is positive, an additional 10 te
> Explain how to create a probability density histogram.
> Suppose that the police force in Exercise 23 maintains the same height requirements for women as men and that the heights of women in the city are normally distributed, with µ = 65 inches and σ = 1.6 inches. What percentage of the women are eligible for
> Make a small probability table for a discrete random variable X and use it to define E(X ), Var (X ), and the standard deviation of X.
> What is a discrete random variable?
> What is a probability table?
> What is Pr (X = n) for a geometric random variable with parameter p (the probability of success)? What is E(X ) in this case?
> What is Pr (X = n) for a Poisson random variable with parameter λ? What is E(X ) in this case?
> How is an integral involving a normal density function converted to an integral involving a standard normal density function?
> What is a standard normal random variable? Write the density function.
> What is the density function for a normal random variable with mean µ and standard deviation σ?
> What is the expected value of an exponential random variable?
> What is an exponential density function? Give an example.
> The men hired by a certain city police department must be at least 69 inches tall. If the heights of adult men in the city are normally distributed, with µ = 70 inches and σ = 2 inches, what percentage of the men are tall enough to be eligible for recrui
> Give two ways to compute the variance of a continuous random variable.
> How is the expected value of a continuous random variable computed?
> What is a cumulative distribution function, and how is it related to the corresponding probability density function?
> How is a probability density function used to calculate probabilities?
> What are the two properties of a probability density function?
> What is the difference between a discrete random variable and a continuous random variable?
> Repeat Exercise 2 with λ = .75 and make a histogram. Exercise 2: Let X be a Poisson random variable with parameter λ = 5. Compute the probabilities p0, … , p6 to four decimal places.
> Let X be a Poisson random variable with parameter λ = 5. Compute the probabilities p0, … , p6 to four decimal places.
> Suppose that a random variable X has a Poisson distribution with λ = 3, as in Example 1. Compute the probabilities p6, p7, p8.
> The number of accidents occurring each month at a certain intersection is Poisson distributed with λ = 4.8. (a) During a particular month, are five accidents more likely to occur than four accidents? (b) What is the probability that more than eight acc
> A certain machine part has a nominal length of 80 millimeters, with a tolerance of {.05 millimeter. Suppose that the actual length of the parts supplied is a normal random variable with mean 79.99 millimeters and standard deviation .02 millimeter. How ma
> The number of babies born each day in a certain hospital is Poisson distributed with λ = 6.9. (a) During a particular day, are 7 babies more likely to be born than 6 babies? (b) What is the probability that at most 15 babies will be born during a parti
> The number of people arriving during a 5-minute interval at a supermarket checkout counter is Poisson distributed with λ = 8. (a) What is the probability that exactly eight people arrive during a particular 5-minute period? (b) What is the probability t
> The number of times a printing press breaks down each month is Poisson distributed with λ = 4. What is the probability that the printing press breaks down between 2 and 8 times during a particular month?
> Let X be a Poisson random variable with parameter l. Use Exercise 23 in Section 11.5 to show that the probability that X is an even integer (including 0) is e-λ cosh λ. Exercise 23: The hyperbolic cosine of x, denoted by cosh x, is defined by cosh x = ½
> Let X be a geometric random variable with parameter p. Derive the formula for E(X) by using the power series formula (see Example 3 in Section 11.5): 1 + 2x + 3x2 + … = 1/(1 - x)2 for |x| < 1.
> A person shooting at a target has five successive hits and then a miss. If x is the probability of success on each shot, the probability of having five successive hits followed by a miss is x5(1 - x). Take first and second derivatives to determine the va
> In a production process, a box of fuses is examined and found to contain two defective fuses. Suppose that the probability of having two defective fuses in a box selected at random is (λ2/2) e-λ for some λ. Take first and second derivatives to determine

