Question: Find support reactions at A and B
Find support reactions at A and B and then calculate the axial force N, shear force V, and bending moment M at mid-span of AB. Let L = 4 m, q0 = 160 N/m , P = 200 N, and Mo = 380 Nm?.
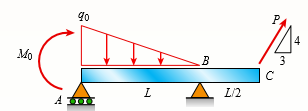
Transcribed Image Text:
Mo B L/2
> A particle moves with position function s = t4 - 4t3 - 20t2 + 20t t ≥ 0 (a) At what time does the particle have a velocity of 20 m/s? (b) At what time is the acceleration 0? What is the significance of this value of t?
> Show that the inflection points of the curve y = (sin x)/x lie on the curve y2 (x4 + 4) = 4.
> Show that x2y2 (4 - x2)(4 - y2) ≤ 16 for all numbers x and y such that |x | ≤ 2 and |y | ≤ 2.
> Does the function f (x) = e10| x-2| - x2 have an absolute maximum? If so, find it. What about an absolute minimum?
> Show that |sin x - cos x | ≤ 2 for all x.
> Assume that a snowball melts so that its volume decreases at a rate proportional to its surface area. If it takes three hours for the snowball to decrease to half its original volume, how much longer will it take for the snowball to melt completely?
> Given a sphere with radius r, find the height of a pyramid of minimum volume whose base is a square and whose base and triangular faces are all tangent to the sphere. What if the base of the pyramid is a regular n-gon? (A regular n-gon is a polygon with
> One of the problems posed by the Marquis de l’Hospital in his calculus textbook Analyse des Infiniment Petits concerns a pulley that is attached to the ceiling of a room at a point C by a rope of length r. At another point B on the ceil
> For what values of c is there a straight line that intersects the curve y = x4 + cx3 + 12x2 - 5x + 2 in four distinct points?
> If a rock is thrown vertically upward from the surface of Mars with velocity 15 m/s, its height after t seconds is h = 15t - 1.86t2. (a) What is the velocity of the rock after 2 s? (b) What is the velocity of the rock when its height is 25 m on its way u
> The speeds of sound c1 in an upper layer and c2 in a lower layer of rock and the thickness h of the upper layer can be determined by seismic exploration if the speed of sound in the lower layer is greater than the speed in the upper layer. A dynamite cha
> Let f(x) = a1 sin x + a2 sin 2x + ∙ ∙ ∙ + an sin nx, where a1, a2, . . . , an are real numbers and n is a positive integer. If it is given that | f (x) | ≤ |sin x | for all x, show that |a1 + 2a2 + ∙ ∙ ∙ + nan | ≤ 1
> For which positive numbers a does the curve y = ax intersect the line y = x?
> ABCD is a square piece of paper with sides of length 1 m. A quarter-circle is drawn from B to D with center A. The piece of paper is folded along EF, with E on AB and F on AD, so that A falls on the quarter-circle. Determine the maximum and minimum areas
> The line y = mx + b intersects the parabola y = x2 in points A and B. (See the figure.) Find the point P on the arc AOB of the parabola that maximizes the area of the triangle PAB. y y=x? B A y = mx +b
> Use a computer with three-dimensional graphing software to graph the surface. Experiment with viewpoints and with domains for the variables until you get a good view of the surface. -4x2 - y2 + z2 = 1
> Sketch the region in the plane consisting of all points (x, y) such that 2xy ≤ |x - y | ≤ x2 + y2
> An isosceles triangle is circumscribed about the unit circle so that the equal sides meet at the point s0, ad on the y-axis (see the figure). Find the value of a that minimizes the lengths of the equal sides. (You may be surprised that the result does no
> For what values of c does the curve y = cx3 + ex have inflection points?
> If a ball is thrown vertically upward with a velocity of 80 ft/s, then its height after t seconds is s = 80t - 16t2. (a) What is the maximum height reached by the ball? (b) What is the velocity of the ball when it is 96 ft above the ground on its way up?
> If P(a, a2) is any point on the parabola y = x2, except for the origin, let Q be the point where the normal line at P intersects the parabola again (see the figure). (a) Show that the y-coordinate of Q is smallest when a = 1/ 2 . (b) Show that the line s
> Sketch the set of all points (x, y) such that |x + y | ≤ ex.
> Find the highest and lowest points on the curve x2 + xy + y2 = 12.
> Calculate the given quantity if a = i + j - 2k b = 3i - 2j + k c = j - 5k (a). 2a + 3b (b). |b | (c). a ∙ b (d). a × b (e). |b × c | (f). a ∙ (b × c) (g). c × c (h). a × (b × c) (i). compa b (j). proja b (k). The angle between a and b (correct to th
> Differentiate the function. f (x) = ln (1/x)
> (a). Find an equation of the sphere that passes through the point (6, -2, 3) and has center (-1, 2, 1). (b). Find the curve in which this sphere intersects the yz-plane. (c). Find the center and radius of the sphere x2 + y2 + z2 - 8x + 2y + 6z + 1 = 0
> An ellipsoid is created by rotating the ellipse 4x2 + y2 – 16 about the x-axis. Find an equation of the ellipsoid.
> (a). Find an equation of the plane that passes through the points A (2, 1, 1), B (-1, -1, 10), and C (1, 3, -4). (b). Find symmetric equations for the line through B that is perpendicular to the plane in part (a). (c). A second plane passes through (2, 0
> Find an equation of the plane through the line of intersection of the planes x - z = 1 and y + 2z = 3 and perpendicular to the plane x + y - 2z = 1.
> The height (in meters) of a projectile shot vertically upward from a point 2 m above ground level with an initial velocity of 24.5 m/s is h = 2 + 24.5t - 4.9t2 after t seconds. (a) Find the velocity after 2 s and after 4 s. (b) When does the projectile r
> Determine whether the lines given by the symmetric equations are parallel, skew, or intersecting. x - х — 1 у - 2 г-3 y z - 3 2 3 4 у — 3 y -1 х+1 z + 5
> Find the distance from the origin to the line x = 1 + t, y = 2 - t, z = 21 + 2t.
> Find the point in which the line with parametric equations x = 2 - t, y = 1 + 3t, z = 4t intersects the plane 2x - y + z = 2.
> Find an equation of the plane. The plane through (1, 2, -2) that contains the line x = 2t, y = 3 - t, z = 1 + 3t
> Find an equation of the plane. The plane through (3, -1, 1), (4, 0, 2), and (6, 3, 1)
> Reduce the equation to one of the standard forms, classify the surface, and sketch it. x2 - y2 - z2 - 4x - 2z + 3 = 0
> A boat is pulled onto shore using two ropes, as shown in the diagram. If a force of 255 N is needed, find the magnitude of the force in each rope. 20° 255 N 30°
> Find the acute angle between two diagonals of a cube.
> Show that if a, b, and c are in V3, then (a × b) ∙ [(b × c) × (c × a) g = [a ∙ (b × c)]2
> Suppose that u ∙ (v × w) = 2. Find (a). (u × v) ∙ w (b). u ∙ (w × v) (c). v ∙ (u × w) (d). (u × v) ∙ v
> (a). Sketch the graph of y = ex as a curve in R2. (b). Sketch the graph of y = ex as a surface in R3. (c). Describe and sketch the surface z = ey.
> Differentiate the function. y = 1 / ln x
> (a). What does the equation y = x2 represent as a curve in R2? (b). What does it represent as a surface in R3? (c). What does the equation z = y2 represent?
> Show that the curve of intersection of the surfaces x2 + 2y2 - z2 + 3x = 1 and 2x2 + 4y2 - 2z2 - 5y = 0 lies in a plane.
> Show that if the point (a, b, c) lies on the hyperbolic paraboloid z = y2 - x2, then the lines with parametric equations x = a + t, y = b + t, z = c + 2 (b 0- a) t and x = a + t, y = b - t, z = c – 2 (b + a) t both lie entirely on this paraboloid. (This
> A cooling tower for a nuclear reactor is to be constructed in the shape of a hyperboloid of one sheet (see the photo on page 839). The diameter at the base is 280 m and the minimum diameter, 500 m above the base, is 200 m. Find an equation for the tower.
> Sketch the graph of a function that satisfies the given conditions. f (0) = 0, f ‘(-2) = f ‘(1) = f ‘(9) = 0, lim f(x) = 0, lim f(x) = -∞, f'(x) < 0 on (-o0, -2), (1, 6), and (9, 0), f'(x) > 0 on
> Segments AB and BCD of beam ABCD are pin connected at x = 4 m. The beam is supported by a sliding support at A and roller supports at C and D (see figure). A triangularly distributed load with peak intensity of 80 N/m acts on BC. A concentrated moment is
> Segments AB and BC of beam ABC are pin connected a small distance to the right of joint B (see figure). Axial loads act at A and at the mid-span of AB. A concentrated moment is applied at joint B. (a) Find reactions at supports A, B, and C. (b) Find inte
> Find support reactions at A and B and then calculate the axial force N, shear force V, and bending moment M at mid-span of AB. Let L = 14 ft, qo 512 lb/ft, P = 50 lb, and M0 = 300 lb-ft. Mo 4 B 3 C L L/2 A
> Two separate cables AC and BC support a sign structure of weight W = 1575 lb attached to a building. The sign is also supported by a pin support at O and a lateral restraint in the z-direction at D. (a) Find the tension in each cable. Neglect the mass of
> A round bar ABC of length 2L (see figure) rotates about an axis through the midpoint C with constant angular speed ω (radians per second). The material of the bar has weight density g. (a) Derive a formula for the tensile stress x s in the bar
> Two gondolas on a ski lift are locked in the position show in the figure while repairs are being made elsewhere. The distance between support towers is L 5100 ft. The length of each cable segment under gondolas weighing WB = 450 lb and WC =650 lb are DAB
> A crane boom of mass 450 kg with its center of mass at C is stabilized by two cables AQ and BQ (Ae = 304 mm2 for each cable) as shown in the figure. A load P = 20 kN is supported at point D. The crane boom lies in the y-z plane. (a) Find the tension forc
> An L-shaped reinforced concrete slab 12 ft × 12 ft, with a 6 ft × 6 ft cut-out and thickness t = 9.0 in, is lifted by three cables attached at O, B, and D, as shown in the figure.
> Solve the preceding problem if the mass of the tailgate is MT = 27 kg and that of the crate is MC = 68 kg. Use dimensions H = 305 mm, LÂ =Â 406Â mm, dCÂ =Â 460 mm, and dT = 350 mm. The cable cross-se
> A cable and pulley system at D is used to bring a 230-kg pole (ACB) to a vertical position, as shown in the figure part a. The cable has tensile force T and is attached at C. The length L of the pole is 6.0Â m, the outer diameter is d = 140 mm
> A pickup truck tailgate supports a crate where WC = 150 lb, as shown in the figure. The tailgate weighs WT = 60 lb and is supported by two cables (only one is shown in the figure). Each cable has an effective cross-sectional area AE = 0.017 in2. (a) Find
> A long retaining wall is braced by wood shores set at an angle of 308 and supported by concrete thrust blocks, as shown in the first part of the figure. The shores are evenly spaced at 3 m apart. For analysis purposes, the wall and shores are idealized a
> Two steel wires support a moveable overhead camera weighing W = 28 lb (see figure part a) used for close-up viewing of field action at sporting events. At some instant, wire 1 is at an angle a = 228 to the horizontal and wire 2 is at angle b = 408. Wires
> A car weighing 130 kN when fully loaded is pulled slowly up a steep inclined track by a steel cable (see figure). The cable has an effective cross-sectional area of 490 mm2, and the angle a of the incline is 308. (a) Calculate the tensile stress st in th
> The cross section of a concrete corner column that is loaded uniformly in compression is shown in the figure. A circular pipe chase cut-out of 10 in. in diameter runs the height of the column (see figure). (a) Determine the average compression stress c s
> A circular aluminum tube with a length of L = 420 mm is loaded in compression by forces P (see figure). The hollow segment of length L/3 has outside and inside diameters of 60 mm and 35 mm, respectively. The solid segment of length 2L/3 has a diameter of
> A bicycle rider wants to compare the effectiveness of cantilever hand brakes (see figure part a) versus V brakes (figure part b). (a) Calculate the braking force RB at the wheel rims for each of the bicycle brake systems shown. Assume that all forces act
> A force P of 70 N is applied by a rider to the front hand brake of a bicycle (P is the resultant of an evenly distributed pressure). As the hand brake pivots at A, a tension T develops in the 460-mm long brake cable (Ae = 1 .075 mm2), which elongates by
> A circular tube AB is fixed at one end and free at the other end. The tube is subjected to axial force at joint B. If the outer diameter of the tube is 3 in. and the thickness is ¾ in., calculate the maximum normal stress in the
> A circular nylon pipe supports a downward load PA = 10 kN, which is uniformly distributed around a cap plate at the top of the lower pipe. A second load PB = 20 kN is applied upward at the top. The inner and outer diameters of the upper and lower parts o
> A square steel tube of a length L = 20 ft and width b2 = 10.0 in. is hoisted by a crane (see figure). The tube hangs from a pin of diameter d that is held by the cables at points A and B. The cross section is a hollow square with an inner dimension b1 =
> The data shown in the accompanying table are from a tensile test of high-strength steel. The test specimen has a diameter of 0.505 in. and a gage length of 2.00 in. At fracture, the elongation between the gage marks is 0.12Â in. and the minimu
> A specimen of a methacrylate plastic is tested in tension at room temperature (see figure), producing the stress-strain data listed in the accompanying table. Plot the stress-strain curve and determine the proportional limit, modulus of elasticity (which
> A symmetrical framework consisting of three pin-connected bars is loaded by a force P (see figure). The angle between the inclined bars and the horizontal is 52 a 58. The axial strain in the middle bar is measured as 0.036. Determine the tensile stress i
> The strength-to-weight ratio of a structural material is defined as its load-carrying capacity divided by its weight. For materials in tension, use a characteristic tensile stress obtained from a stress strain curve as a measure of strength. For instance
> Three different materials, designated A, B, and C, are tested in tension using test specimens having diameters of 0.505 in. and gage lengths of 2.0 in. (see figure). At failure, the distances between the gage marks are found to be 2.13, 2.48, and 2.78 in
> A steel riser pipe hangs from a drill rig located offshore in deep water. (a) What is the greatest length (meters) it can have without breaking if the pipe is suspended in the air and the ultimate strength (or breaking strength) is 550 MPa? (b) If the sa
> A wire of length L = 4 ft and diameter d = 0.125 in. is stretched by tensile forces P = 600 lb. The wire is made of a copper alloy having a stress strain relationship that may be described mathematically by in which ε
> A continuous cable (diameter 6 mm) with tension force T is attached to a horizontal frame member at B and C to support a sign structure. The cable passes over a small frictionless pulley at D. The wire is made of a copper alloy, and the stress-strain rel
> An aluminum bar has length L = 6 ft and diameter d = 1.375 in. The stress-strain curve for the aluminum is shown in Fig. 1-34. The initial straight line part of the curve has a slope (modulus of elasticity) of 10.61 063 psi. The bar is loaded
> A circular bar of magnesium alloy is 750 mm long. The stress-strain diagram for the material is shown in the figure. The bar is loaded in tension to an elongation of 6.0 mm, and then the load is removed. (a) What is the permanent set of the bar? (b) If t
> A suspender on a suspension bridge consists of a cable that passes over the main cable (see figure) and supports the bridge deck, which is far below. The suspender is held in position by a metal tie that is prevented from sliding downward by clamps aroun
> A bar made of structural steel having the stress-strain diagram shown in the figure has a length of 48 in. The yield stress of the steel is 42 ksi, and the slope of the initial linear part of the stress-strain curve (modulus of elasticity) is 30 Ã
> A bar of length 2.0 m is made of a structural steel having the stress-strain diagram shown in the figure. The yield stress of the steel is 250 MPa, and the slope of the initial linear part of the stress-strain curve (modulus of elasticity) is 200 GPa. Th
> Three round, copper alloy bars having the same length L but different shapes are shown in the figure. The first bar has a diameter d over its entire length, the second has a diameter d over one-fifth of its length, and the third has a diameter d over one
> A hollow, brass circular pipe ABC (see figure) supports a load P1 = 26.5 kips acting at the top. A second load P2 = 22.0 kips is uniformly distributed around the cap plate at B. The diameters and thicknesses of the upper and lower parts of the pipe are d
> A tensile test is performed on a brass specimen 10 mm in diameter using a gage length of 50 mm (see figure). When the tensile load P reaches a value of 20 kN, the distance between the gage marks has increased by 0.122 mm. (a) What is the modulus of elast
> A bar of monel metal with a length LÂ = 9Â in. and a diameter d = 0.225 in. is loaded axially by a tensile force P (see figure). If the bar elongates by 0.0195 in., what is the decrease in diameter d? What is the magnitude of the lo
> A circular aluminum tube of length LÂ =Â 600Â mm is loaded in compression by forces P (see figure). The outside and inside diameters are d2 = 75 mm and d1 = 63 mm, respectively. A strain gage is placed on the outside of t
> A polyethylene bar having rectangular cross section with a width 7.35 in. and depth 7 in. is placed inside a hollow steel square section with side dimension of 8 in. The polyethylene bar is then compressed by an axial force P. At what value o
> A square plastic bar (length Lp, side dimension sp = 193 mm) is inserted inside a hollow, square, cast iron tube (length Lc = 400 mm, side sc = 200 mm, and thickness tc = 3 mm). (a) What is the required initial length Lp of the plastic bar so that, when
> A polyethylene bar with a diameter d1 = 4.0 in. is placed inside a steel tube with an inner diameter d2 = 4.01 in. (see figure). The polyethylene bar is then compressed by an axial force P. At what value of the force P will the space between the polyethy
> Continuous cable ADB runs over a small frictionless pulley at D to support beam OABC that is part of an entrance canopy for a building (see figure). Assume that the canopy segment has a weight W = 1700 lb. (a) Find the required cross-sectional area of ca
> A round bar of 10 mm diameter is made of aluminum alloy 7075-T6 (see figure). When the bar is stretched by axial forces P, its diameter decreases by 0.016 mm. Find the magnitude of the load P. Obtain the material properties from Appendix I. |d= 10 m
> A high-strength steel bar used in a large crane has a diameter d = 2.00 in. (see figure). The steel has a modulus of elasticity E = 29 × 106 psi and Poisson’s ratio is n = 0.29. Because of clearance requirements, the diamet
> A bicycle chain consists of a series of small links, where each are 12 mm long between the centers of the pins (see figure). You might wish to examine a bicycle chain and observe its construction. Note particularly the pins, which have a diameter of 2.5
> A basketball player hangs on the rim after a dunk. He applies equal forces P1 = P2 = 110 lb at both A and B (see joint coordinates in the figure). Forces P1Â and P2 act parallel to the y-z plane. (a) Find the reactions at the support bracket (
> A cargo ship is tied down to marine bollards at a number of points along its length while its cargo is unloaded by a container handling crane. Each bollard is fastened to the wharf using anchor bolts. Three cables having known tension force magnitudes F1
> The top portion of a pole saw used to trim small branches from trees is shown in the figure part a. The cutting blade BCD (see figure parts a and c) applies a force P at point D. Ignore the effect of the weak return spring attached to the cut
> A single steel strut AB with a diameter ds = 8mm supports the vehicle engine hood of a mass 20 kg that pivots about hinges at C and D (see figure parts a and b). The strut is bent into a loop at its end and then attached to a bolt at A with a diameter db
> A spray nozzle for a garden hose requires a force F = 5 lb to open the spring-loaded spray chamber AB. The nozzle hand grip pivots about a pin through a flange at O. Each of the two flanges has a thickness t = 1/16 in., and the pin has a diameter dp = 1/
> A removable sign post on a hurricane evacuation route (see figure part a) consists of an upper pole with a slotted base plate bolted to a short post anchored in the ground. The lower post is capped with a separate conventional base plate having four hole
> A shock mount constructed as shown in the figure is used to support a delicate instrument. The mount consists of an outer steel tube with inside diameter b, a central steel bar of diameter d that supports the load P, and a hollow rubber cylinder (height&

