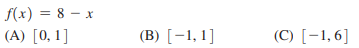[SOLVED] find the absolute maximum and absolute minimum

> A 300-room hotel in Las Vegas is filled to capacity every night at $80 a room. For each $1 increase in rent, 3 fewer rooms are rented. If each rented room costs $10 to service per day, how much should the management charge for each room to maximize gross

> A university student center sells 1,600 cups of coffee per day at a price of $2.40. (A) A market survey shows that for every $0.05 reduction in price, 50 more cups of coffee will be sold. How much should the student center charge for a cup of coffee in

> The following table contains priceâ demand and total cost data for the production of regular sleeping bags, where p is the wholesale price (in dollars) of a sleeping bag for an annual demand of x sleeping bags and C is the total cost (i

> Repeat Problem 21 for Data from Problem 21: (A) Find the maximum revenue. (B) Find the maximum profit, the production level that will realize the maximum profit, and the price the company should charge for each television set. (C) If the government de

> A company manufactures and sells x cameras per week. The weekly price–demand and cost equations are, respectively, p = 400 - 0.5x and C(x) = 2,000 + 200x (A) What price should the company charge for the cameras, and how many cameras should be produced

> Find the dimensions of a rectangle with a perimeter of 76 feet that has the maximum area.

> Find the dimensions of a rectangle with an area of 108 square feet that has the minimum perimeter.

> Find two positive numbers whose product is 19 and whose sum is a minimum.

> Refer to the graph of y =ï¦(x) shown here. Find the absolute minimum and the absolute maximum over the indicated interval.

> There are 10 senators (half Democrats, half Republicans) and 16 representatives (half Democrats, half Republicans) who wish to serve on a joint congressional committee on tax reform. An 8-person committee is chosen at random from those who wish to serve.

> Refer to the graph of y =ï¦(x) shown here. Find the absolute minimum and the absolute maximum over the indicated interval.

> by inspecting the graph of the function, find the absolute maximum and absolute minimum on the given interval.

> Describe the graph of ï¦ at the given point relative to the existence of a local maximum or minimum with one of the following phrases: âLocal maximum,â âLocal minimum,â&#

> A single card is drawn from a standard 52-card deck. find the conditional probability that. The card is red, given that it is a jack.

> find the absolute maximum and minimum, if either exists, for each function on the indicated intervals.

> find the indicated extremum of each function on the given interval.

> Because of limited funds, 5 research centers are to be chosen out of 8 suitable ones for a study on heart disease. If the selection is made at random, what is the probability that 5 particular research centers will be chosen?

> find the indicated extremum of each function on the given interval.

> find the absolute extremum, if any, given by the second derivative test for each function.

> A single card is drawn from a standard 52-card deck. find the conditional probability that. The card is a jack, given that it is red.

> find the absolute extremum, if any, given by the second derivative test for each function.

> find the absolute maximum and absolute minimum of each function on the given interval.

> find the absolute maximum and absolute minimum of each function on the indicated intervals.

> Refer to the graph of y =ï¦(x) shown here. Find the absolute minimum and the absolute maximum over the indicated interval.

> find the domain of the function and all x or y intercepts.

> A 4-person grievance committee is to include employees in 2 departments, A and B, with 15 and 20 employees, respectively. If the 4 people are selected at random from the 35 employees, what is the probability of selecting (A) 3 from A and 1 from B? (B)

> find the domain of the function and all x or y intercepts.

> In a study on the speed of muscle contraction in frogs under various loads, researchers found that the speed of contraction decreases with increasing loads. More precisely, they found that the relationship between speed of contraction, S (in centimeters

> A doctor prescribes a 1,000 mg pill every twelve hours. The concentration of the drug (in parts per million) in the bloodstream t hours after ingesting the pill is (A) Graph D(t). (B) What is the concentration after 12 hours? (C) What is the maximum

> The total daily cost (in dollars) of producing x city bikes is given by C(x) = 500 + 2x + 0.2x2 (A) Sketch the graphs of the average cost function and the marginal cost function on the same set of coordinate axes. Include any oblique asymptotes. (B) Fin

> The management of a manufacturing plant wishes to add a fenced-in rectangular storage yard of 20,000 square feet, using a building as one side of the yard (see the figure). If x is the distance (in feet) from the building to the fence, show that the leng

> A company producing dive watches has established that, on average, a new employee can assemble N(t) dive watches per day after t days of on-the-job training, as given by (A) Where is N(t) increasing? Decreasing? (B) Where is the graph of N concave up

> Suppose that the cost function C(x) (in dollars) for the company in Problem 79 is C(x) = 830 + 396x (A) Write an equation for the profit P(x). (B) Graph the profit function P

> summarize all pertinent information obtained by applying the graphing strategy and sketch the graph of y =ï¦(x) . [Note: These rational functions are not reduced to lowest terms.]

> A single card is drawn from a standard 52-card deck. find the conditional probability that. The card is a face card, given that it is red.

> summarize all pertinent information obtained by applying the graphing strategy and sketch the graph of y =ï¦(x) . [Note: These rational functions are not reduced to lowest terms.]

> for the given cost function C(x), find the oblique asymptote of the average cost function C(x).

> show that the line y = x is an oblique asymptote for the graph of y = ï¦(x), summarize all pertinent information obtained by applying the graphing strategy, and sketch the graph of y = ï¦(x).

> Summarize the pertinent information obtained by applying the graphing strategy and sketch the graph of y =ï¦(x).

> Six popular brands of cola are to be used in a blind taste study for consumer recognition. (A) If 3 distinct brands are chosen at random from the 6 and if a consumer is not allowed to repeat any answers, what is the probability that all 3 brands could b

> Summarize the pertinent information obtained by applying the graphing strategy and sketch the graph of y =ï¦(x).

> A single card is drawn from a standard 52-card deck. find the conditional probability that. The card is red, given that it is a face card

> A circular spinner is divided into 15 sectors of equal area: 6 red sectors, 5 blue, 3 yellow, and 1 green. , consider the experiment of spinning the spinner once. Find the probability that the spinner lands on: Red or Blue.

> Summarize the pertinent information obtained by applying the graphing strategy and sketch the graph of y =ï¦(x).

> use the given information to sketch the graph of ï¦. Assume that ï¦ is continuous on its domain and that all intercepts are included in the table of values

> Several experiments are simulated using the random number feature on a graphing calculator. For example, the roll of a fair die can be simulated by selecting a random integer from 1 to 6, and 50 rolls of a fair die by selecting 50 random integers from 1

> use the given information to sketch the graph of ï¦. Assume that ï¦ is continuous on its domain and that all intercepts are included in the table of values

> use the given information to sketch a possible graph of ï¦.

Question: find the absolute maximum and absolute minimum