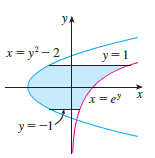
Question: Find the area of the shaded region. /
> Suppose f is continuous on [0, ∞] and limx→∞f (x) = 1. Is it possible that f∞0f (x) dx is convergent?
> Show how to approximate the required work by a Riemann sum. Then express the work as an integral and evaluate it. A heavy rope, 50 ft long, weighs 0.5 lb/ft and hangs over the edge of a building 120 ft high. (a). How much work is done in pulling the rope
> Each integral represents the volume of a solid. Describe the solid. (a) 7 y dy (b) 7 [(1 (1 + cos x)? – 1°]dx
> For any number c, we let fc (x) be the smaller of the two numbers (x – c)2 and (x – c – 2)2. Then we define Find the maximum and minimum values of g (c) if -2 g(c) f.(x)dx
> Each integral represents the volume of a solid. Describe the solid. *w/2 (а) т cos?x dx (b) (y* – y*) dy
> Use a computer algebra system to find the exact volume of the solid obtained by rotating the region bounded by the given curves about the specified line. y = x, y = xel-/2, about y = 3
> Use a graph to find approximate -coordinates of the points of intersection of the given curves. Then use your calculator to find (approximately) the volume of the solid obtained by rotating about the -axis the region bounded by these curves. y = 3 s
> Use a graph to find approximate -coordinates of the points of intersection of the given curves. Then use your calculator to find (approximately) the volume of the solid obtained by rotating about the -axis the region bounded by these curves. y = 2 +
> Set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. y = cos x, y = 2 – cos x, 0<I< 27; about y 4
> Set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. x² – y? = 1, x= 3; about x = -2
> The region enclosed by the given curves is rotated about the specified line. Find the volume of the resulting solid. y = x', y = Vx; about y = 1
> The region enclosed by the given curves is rotated about the specified line. Find the volume of the resulting solid. y = x', y = Vx; about x = 1
> The region enclosed by the given curves is rotated about the specified line. Find the volume of the resulting solid. x= y?, x = 1; about x = 1
> Use Newton’s method to find all the roots of the equation correct to eight decimal places. Start by drawing a graph to find initial approximations. 3 sin(x?) = 2x
> When gas expands in a cylinder with radius r, the pressure at any given time is a function of the volume: P = P (V). The force exerted by the gas on the piston (see the figure) is the product of the pressure and the area: F = πr2p. Show that t
> The region enclosed by the given curves is rotated about the specified line. Find the volume of the resulting solid. х — у— 1, у— х? — 4х + 3; about y— 3
> The region enclosed by the given curves is rotated about the specified line. Find the volume of the resulting solid. x = 2y – y', x = 0; about the y-axis
> The region enclosed by the given curves is rotated about the specified line. Find the volume of the resulting solid. у 3 1/х, х 3D 1, х— 2, у %3D 0; about the x-axis
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. y = x, y = Vx; about x = 2
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. у 3D1+ sec x, yу 3 3; about y —1
> Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line. Sketch the region, the solid, and a typical disk or washer. y = e", y = 1, x = 2; about y = 2
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. x=1- y, x= y² – 1
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. у %3 х? — 2х, у%3х+4
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. y = x², y? = x
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. у 3 In x, ху — 4, х%3D1, х— 3
> A spinner from a board game randomly indicates a real number between 0 and 10. The spinner is fair in the sense that it indicates a number in a given interval with the same probability as it indicates a number in any other interval of the same length.
> Let g (x) = fx0f (t) dt, where f is the function whose graph is shown. (a). Evaluate g (0) and g (6). (b). Estimate g (x) for x = 1, 2, 3, 4, and 5. (c). On what interval g is increasing? (d). Where does have a maximum value? (e). Sketch a rough graph of
> Find the values of p for which the integral converges and evaluate the integral for those values of p. dx
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. y = e", y = x? – 1, x=-1, x = 1 x = -1,
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. sin?x - dx V- x,
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. sec'x -dx lo xVx
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. 2 + e -
> Use the Comparison Theorem to determine whether the integral is convergent or divergent. x' + 1 .3
> Show that 1/3 Tn + 3.2Mn = S2n.
> Find the number b such that the line y = b divides the region bounded by the curves y = x2 and y = 4 into two regions with equal area.
> Sketch the region and find its area (if the area is finite). s = {(x, y) | –2 < r< 0, 0 < y< 1//I + 2 }
> A container in the shape of an inverted cone has height 16 cm and radius 5 cm at the top. It is partially filled with a liquid that oozes through the sides at a rate proportional to the area of the container that is in contact with the liquid. (The surfa
> Find the area of the shaded region. YA x= y? - 4y (-3, 3) x= 2y - y?
> Let g (x) = fx0 f (t) dt, where f is the function whose graph is shown. (a). Evaluate g (x) for x = 0, 1, 2, 3, 4, 5 and 6. (b). Estimate g (7). (c). Where does b have a maximum value? Where does it have a minimum value? (d). Sketch a rough graph of g.
> Sketch the region and find its area (if the area is finite). S = {(x, y) | 0 < x < n/2, 0 < y< sec?r}
> Sketch the region and find its area (if the area is finite). S = {(x, y) | x > 0, 0 < y< xe*}
> Sketch the region and find its area (if the area is finite). S = {(x, y) | 0 < y < 2/(x² + 9)}
> Find the area enclosed by the x-axis and the curve x = 1 + et, y = t – t2.
> Find the area enclosed by the curve x = t2 – 2t, y = √t and the y-axis.
> Use the parametric equations of an ellipse, x = a cos θ, y = b sin θ, 0 < θ < 2π, to find the area that it encloses.
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. csc x dx J2/2
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. dx e - 1
> Graph f (x) = sin (ex) and use the graph to estimate the value of t such that ft+1tf (x) dx is a maximum. Then find the exact value of t that maximizes this integral.
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1 dy 4y – 1 Je
> A model rocket is fired vertically upward from rest. Its acceleration for the first three seconds is a (t) = 60t, at which time the fuel is exhausted and it becomes a freely “falling” body. Fourteen seconds later, the rocket’s parachute opens, and the (d
> If the birth rate of a population is b (t) = 2200e0.024t people per year and the death rate is d (t) = 1460e0.018t people per year, find the area between these curves for 0 < t < 10. What does this area represent?
> A cross-section of an airplane wing is shown. Measurements of the thickness of the wing, in centimeters, at 20-centimeter intervals are 5.8, 20.3, 26.7, 29.0, 29.0, 27.6, 26.3, 28.8, 20.5, 15.1, 8.7 and 2.8. Use Simpson’s Rule to estima
> The widths (in meters) of a kidney-shaped swimming pool were measured at 2-meter intervals as indicated in the figure. Use Simpson’s Rule to estimate the area of the pool. 5.6 5.0 6.8 4.8 4.8 7.2 6.2
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1 dx 3— х
> Racing cars driven by Chris and Kelly are side by side at the start of a race. The table shows the velocities of each car (in miles per hour) during the first ten seconds of the race. Use Simpson’s Rule to estimate how much farther Kell
> Sketch the curves y = cos x and y = 1 – cos x, 0 < x < π, and observe that the region between them consists of two separate parts. Find the area of this region.
> Sketch the region that lies between the curves y = cos x and y = sin 2x and between x = 0 and x = π/2. Notice that the region consists of two separate parts. Find the area of this region.
> Show that f10(1 – x2) n dx = 22n(n!)2/ (2n + 1)! Hint: Start by showing that if denotes the integral, then 2k + 2 - Ik 2k + 3 Ik+1
> Use a graph to find approximate x-coordinates of the points of intersection of the given curves. Then find (approximately) the area of the region bounded by the curves. y = x cos x, y=x10
> Use a graph to find approximate x-coordinates of the points of intersection of the given curves. Then find (approximately) the area of the region bounded by the curves. y = x² In x, y = VI – I (х — 1
> Use a graph to find approximate x-coordinates of the points of intersection of the given curves. Then find (approximately) the area of the region bounded by the curves. y = y = x* – x, x 0 (x² + 1)*"
> A high-speed bullet train accelerates and decelerates at the rate of 4ft/s2. Its maximum cruising speed is 90 mi/h. (a). What is the maximum distance the train can travel if it accelerates from rest until it reaches its cruising speed and then runs at th
> Find the area of the shaded region. y. y = Vx+2 x= 2 1 х+1
> Use a graph to find approximate x-coordinates of the points of intersection of the given curves. Then find (approximately) the area of the region bounded by the curves. y = x sin(x²), y = x*
> Sketch the region enclosed by the given curves and find its area. y = 3x², y= 8r², 4x + y = 4, x> 0 %3D
> Sketch the region enclosed by the given curves and find its area. y = 1/x, y= x, y=}x, x>0
> Sketch the region enclosed by the given curves and find its area. у %3D сos x, у — 2 — cos x, 0x<2п
> Sketch the region enclosed by the given curves and find its area. y = e", y = xe", x= 0
> A hemispherical bubble is placed on a spherical bubble of radius 1. A smaller hemispherical bubble is then placed on the first one. This process is continued until chambers, including the sphere, are formed. (The figure shows the case n = 4.) Use mathema
> Sketch the region enclosed by the given curves and find its area. y = x', y = 4x – x?
> Sketch the region enclosed by the given curves and find its area. у — 12 — х', у-х*— 6 y= x² – 6
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. у %3 sin x, у— 2х/т, х>0
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. x= 2y', x= 4 + y? %3D
> To prove Theorem 1, let F and G be any two antiderivatives of f on I and let H = G - F. (a). If x1 and x2 are any two numbers in I with x1 < x2, apply the Mean Value Theorem on the interval [x1, x2] to show that H (x1) = H (x2). Why does this show that H
> Sketch the region enclosed by the given curves. Decide whether to integrate with respect to x or y. Draw a typical approximating rectangle and label its height and width. Then find the area of the region. 4x + y? = 12, x= y
> Find the area of the shaded region. yA y = 5x – x? ((4, 4) y=x
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. -/2 e dy
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. J. Tr? + 2)²
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. -1 dw 2 –
> In an automobile race along a straight road, car A passed car B twice. Prove that at some time during the race their accelerations were equal.
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1 dx V1 +x 4.
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 1 (x – 2)2
> Show that ½ (Tn + Mn) = T2n.
> (a). Graph the functions f (x) = 1/x1.1 and g (x) = 1/x0.9 in the viewing rectangles [0, 10] by [0, 1] and [0, 100] by [0, 1]. (b). Find the areas under the graphs of f and g from x = 1 to x = t and evaluate for t =10, 100, 104, 106, 1010, and 1020. (c).
> Sketch the region and find its area (if the area is finite). s = {(x, y) | x > -2, 0 < y<e?}
> If the units for are feet and the units for a (x) are pounds per foot, what are the units for da/dx? What units does f82 a(x) dx have?
> Sketch the region and find its area (if the area is finite). S = {(r, y) | x < 1, 0 < y< e*}
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. In x dx
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. *2 (2' In z dz Jo
> Find the area under the curve y = 1/x3 from x = 1 to x = t and evaluate it for t = 10, 100, and 1000. Then find the total area under this curve for x > 1.
> Find the minimum value of the area of the region under the curve y = x + 1/x from x = a to x = a + 1.5, for all a > 0.
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 33 " (x – 1)-1/5 dx
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. хр (х — 6)° J6 4.
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. *14 dx -2 x + 2
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 3 dx
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. dx. e2* + 3
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. Je x(In x)
> If x is measured in meters and f (x) is measured in newtons, what are the units for f0100 f (x) dx?
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. In x dx .3
> Determine whether each integral is convergent or divergent. Evaluate those that are convergent. x? dx 9 + x*