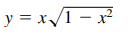Question: Find the derivative of the function. /
> f(t) = 3t + 5, [1, 2] Find the average rate of change of the function over the given interval. Compare this average rate of change with the instantaneous rates of change at the endpoints of the interval.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If f(x) = 0, then f′(x) is undefined.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If f(x) = −g(x) + b, then f′(x) = −g′(x).
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If y = π2 , then dy/dx = 2π.
> Find the derivative of the function.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If y = x a+2 + bx, then dy/dx = (a + 2)x a+1 + b.
> Determine whether the statement is true or false. If it is false, explain why or give an example that shows it is false. If f′(x) = g′(x), then f(x) = g(x).
> Repeat Exercise 83 for the function f(x) = x3 , where T(x) is the line tangent to the graph at the point (1, 1). Explain why the accuracy of the linear approximation decreases more rapidly than in Exercise 83.
> Consider the function f(x) = x3/2 with the solution point (4, 8). (a) Use a graphing utility to graph f. Use the zoom feature to obtain successive magnifications of the graph in the neighborhood of the point (4, 8). After zooming in a few times, the gra
> Find an equation of the tangent line to the graph of the function f through the point (x0, y0) not on the graph. To find the point of tangency (x, y) on the graph of f, solve the equation (x0, y0) = (5, 0)
> Find an equation of the tangent line to the graph of the function f through the point (x0, y0) not on the graph. To find the point of tangency (x, y) on the graph of f, solve the equation f(x) = √x (x0,y0) = ( - 4, 0)
> Show that the graph of the function f (x) = x5 + 3x3 + 5x
> Show that the graph of the function f (x) = 3x + sin x + 2 does not have a horizontal tangent line.
> Show that the graphs of the two equations have tangent lines that are perpendicular to each other at their point of intersection.
> Sketch the graphs of y = x2 and y = −x2 + 6x − 5, and sketch the two lines that are tangent to both graphs. Find equations of these lines.
> Find the derivative of the function.
> Use the graph of f to answer each question. To print an enlarged copy of the graph, go to MathGraphs.com. (a) Between which two consecutive points is the average rate of change of the function greatest? (b) Is the average rate of change of the functio
> Sketch the graph of a function f such that f′ > 0 for all x and the rate of change of the function is decreasing.
> The graphs of a function f and its derivative f′ are shown on the same set of coordinate axes. Label the graphs as f or f′ and write a short paragraph stating the criteria you used in making your selection. To print an
> The graphs of a function f and its derivative f′ are shown on the same set of coordinate axes. Label the graphs as f or f′ and write a short paragraph stating the criteria you used in making your selection. To print an
> g(x) = 3 f(x) − 1 The relationship between f and g is given. Explain the relationship between f′ and g′.
> The relationship between f and g is given. Explain the relationship between f′ and g′. g(x) = −5 f(x)
> The relationship between f and g is given. Explain the relationship between f′ and g′. g(x) = 2 f(x)
> g(x) = f(x) + 6 The relationship between f and g is given. Explain the relationship between f′ and g′.
> Find k such that the line is tangent to the graph of the function. Function: f(x) = k√x Line: y = x + 4
> Find k such that the line is tangent to the graph of the function. Function: / Line: /
> Find the derivative of the function.
> Function: f(x) = kx2 Line: = −2x + 3 Find k such that the line is tangent to the graph of the function.
> Function: f(x) = k − x2 Line: y = −6x + 1 Find k such that the line is tangent to the graph of the function.
> y = √3x + 2 cos x, 0 ≤ x < 2π Determine the point(s) (if any) at which the graph of the function has a horizontal tangent line.
> y = x + sin x, 0 ≤ x < 2π Determine the point(s) (if any) at which the graph of the function has a horizontal tangent line.
> y = x2 + 9 Determine the point(s) (if any) at which the graph of the function has a horizontal tangent line.
> Determine the point(s) (if any) at which the graph of the function has a horizontal tangent line.
> y = x3 + x Determine the point(s) (if any) at which the graph of the function has a horizontal tangent line.
> y = x4 − 2x2 + 3 Determine the point(s) (if any) at which the graph of the function has a horizontal tangent line.
> (a) find an equation of the tangent line to the graph of the function at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results.
> (a) find an equation of the tangent line to the graph of the function at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results.
> Find the derivative of the function.
> (a) find an equation of the tangent line to the graph of the function at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results.
> (a) find an equation of the tangent line to the graph of the function at the given point, (b) use a graphing utility to graph the function and its tangent line at the point, and (c) use the tangent feature of a graphing utility to confirm your results.
> Find the derivative of the function.
> Find the derivative of the function.
> Find the derivative of the function.
> f(x) = 6√x + 5 cos x Find the derivative of the function.
> f(t) = t 2/3 − t 1/3 + 4 Find the derivative of the function.
> f(x) = √x − 6√ 3 x Find the derivative of the function.
> y = x2 (2x2 − 3x) Find the derivative of the function.
> y = x(x2 + 1) Find the derivative of the function.
> Find the derivative of the function.
> Find the derivative of the function.
> Find the derivative of the function.
> Find the derivative of the function.
> Find the derivative of the function.
> Find the derivative of the function.
> f(x) = x3 − 2x + 3x−3 Find the derivative of the function.
> f(x) = x2 + 5 − 3x−2 Find the derivative of the function
> Function: g(t) = −2 cos t + 5 Point: (π, 7) Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results.
> Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results. Function: f(θ) = 4 sin θ − θ. Point: (0, 0 )
> f(x) = x(2x - 5)3 Find the derivative of the function.
> Function: f(x) = 2(x − 4)2 Point: (2, 8) Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results.
> Function: y = 2x4 − 3 Point: (1, -1) Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results.
> Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results. Function: / Point:
> Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results. Function: / Point: (4, 1)
> Find the slope of the graph of the function at the given point. Use the derivative feature of a graphing utility to confirm your results. Function: / Point: (2,2)
> Complete the table to find the derivative of the function. Original Function: / Rewrite: Differentiate: Simplify:
> Complete the table to find the derivative of the function. Original Function: / Rewrite: Differentiate: Simplify:
> Complete the table to find the derivative of the function. Original Function: Rewrite: Differentiate: Simplify:
> Complete the table to find the derivative of the function. Original Function: / Rewrite: Differentiate: Simplify:
> f(x) = x2 (x - 2)7 Find the derivative of the function.
> y = 7x4 + 2 sin x Use the rules of differentiation to find the derivative of the function.
> y = x2 – ½ cos. Use the rules of differentiation to find the derivative of the function.
> g(t) = π cos t Use the rules of differentiation to find the derivative of the function.
> Use the rules of differentiation to find the derivative of the function.
> y = 2x3 + 6x2 − 1 Use the rules of differentiation to find the derivative of the function.
> s(t) = t 3 + 5t 2 − 3t + 8 Use the rules of differentiation to find the derivative of the function.
> y = 4x − 3x3 Use the rules of differentiation to find the derivative of the function.
> g(x) = x2 + 4x3 Use the rules of differentiation to find the derivative of the function.
> y = t 2 − 3t + 1 Use the rules of differentiation to find the derivative of the function.
> f(t) = −3t 2 + 2t − 4 Use the rules of differentiation to find the derivative of the function.
> Find the derivative of the function.
> g(x) = 6x + 3 Use the rules of differentiation to find the derivative of the function.
> f(x) = x + 11 Use the rules of differentiation to find the derivative of the function.
> Use the rules of differentiation to find the derivative of the function.
> Use the rules of differentiation to find the derivative of the function. /
> Use the rules of differentiation to find the derivative of the function.
> Use the rules of differentiation to find the derivative of the function.
> y = x12 Use the rules of differentiation to find the derivative of the function.
> y = x7 Use the rules of differentiation to find the derivative of the function.
> f(x) = −9 Use the rules of differentiation to find the derivative of the function.
> y = 12 Use the rules of differentiation to find the derivative of the function.
> Find the derivative of the function.
> Use the graph to estimate the slope of the tangent line to y = xn at the point (1, 1). Verify your answer analytically. To print an enlarged copy of the graph, go to MathGraphs.com. (a) y = x−1/2 (b) y = x−1
> Use the graph to estimate the slope of the tangent line to y = xn at the point (1, 1). Verify your answer analytically. To print an enlarged copy of the graph, go to MathGraphs.com (a) y = x1/2 (b) y = x3
> Describe the difference between average velocity and velocity.
> What are the derivatives of the sine and cosine functions?
> Explain how to find the derivative of the function f(x) = cxn.
> What is the derivative of a constant function?
> (a)Find an equation of the normal line to the ellipse x2/32 + y2/8 = 1 at the point (4, 2). (b) Use a graphing utility to graph the ellipse and the normal line. (c) At what other point does the normal line intersect the ellipse?
> The graph shows the normal lines from the point (2, 0) to the graph of the parabola x = y2. How many normal lines are there from the point (x0, 0) to the graph of the parabola if (a) x0 = ¼, (b) x0 = ½, and (c) x0 = 1? (d)