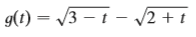Question: Find the domain of the function. /
> A cell phone plan has a basic charge of $35 a month. The plan includes 400 free minutes and charges 10 cents for each additional minute of usage. Write the monthly cost C as a function of the number x of minutes used and graph C as a function of x for 0
> A box with an open top is to be constructed from a rectangular piece of cardboard with dimensions 12 in. by 20 in. by cutting out equal squares of side x at each corner and then folding up the sides as in the figure. Express the volume V of the box as a
> A Norman window has the shape of a rectangle surmounted by a semicircle. If the perimeter of the window is 30 ft, express the area A of the window as a function of the width x of the window.
> Find a formula for the described function and state its domain. An open rectangular box with volume 2m3 has a square base. Express the surface area of the box as a function of the length of a side of the base.
> Find a formula for the described function and state its domain. A closed rectangular box with volume 8 ft3 has length twice the width. Express the height of the box as a function of the width.
> In this section we discussed examples of ordinary, everyday functions: Population is a function of time, postage cost is a function of weight, water temperature is a function of time. Give three other examples of functions from everyday life that are des
> Find a formula for the described function and state its domain. Express the area of an equilateral triangle as a function of the length of a side.
> Find a formula for the described function and state its domain. A rectangle has area 16 m2. Express the perimeter of the rectangle as a function of the length of one of its sides.
> Find a formula for the described function and state its domain. A rectangle has perimeter 20 m. Express the area of the rectangle as a function of the length of one of its sides.
> Find an expression for the function whose graph is the given curve. y 1
> Find an expression for the function whose graph is the given curve. 1
> Find an expression for the function whose graph is the given curve. The top half of the circle x2 + (y – 2)2 = 4
> Find an expression for the function whose graph is the given curve. The bottom half of the parabola x + (y – 1)2 = 0
> Find an expression for the function whose graph is the given curve. The line segment joining the points (-5, 10) and (7, -10)
> Find an expression for the function whose graph is the given curve. The line segment joining the points (1, -3) and (5, 7)
> Sketch the graph of the function. g(x) =||x|- 1|
> Figure 1 was recorded by an instrument operated by the California Department of Mines and Geology at the University Hospital of the University of Southern California in Los Angeles. Use it to estimate the range of the vertical ground acceleration functio
> Sketch the graph of the function. S(x)- |지 if |x| < 1 if |x|>1
> Sketch the graph of the function. h(t) =|t|+ |t + 1|
> Sketch the graph of the function. g(t) = |1 - 3t|
> Sketch the graph of the function. f(x) = |x + 2|
> Sketch the graph of the function. f(x) = x +|x|
> Evaluate f(-3), f(0), and f(2) for the piecewise defined function. Then sketch the graph of the function. |-1 if x<1 f(x) 7- 2x if x>1
> Evaluate f(-3), f(0), and f(2) for the piecewise defined function. Then sketch the graph of the function. x + 1 if x< -1 |x² f(x) = if x> -1
> Evaluate f(-3), f(0), and f(2) for the piecewise defined function. Then sketch the graph of the function. [3 – }x if x<2 f(x)* | 2x – 5 if x> 2
> Evaluate f(-3), f(0), and f(2) for the piecewise defined function. Then sketch the graph of the function. x + 2 if x<0 (x) = - x if x> 0
> Find the domain and sketch the graph of the function. t2 – 1 g(t)- t + 1
> The graphs of f and g are given. a. State the values of f(-4) and g(3). b. For what values of x is f(x) – g(x)? c. Estimate the solution of the equation f(x) = -1. d. On what interval is f decreasing? e. State the domain and range
> Find the domain and sketch the graph of the function. f(x) = 1.6x – 2.4
> Find the domain and range and sketch the graph of the function h(x) = 4 − x2 .
> Find the domain of the function. F(p) — /2 — ур
> Find the domain of the function. u + 1 f(u) = 1 + u + 1
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f is a function, then f(3x) = 3f(x).
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f(s) = f(t), then s = t.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f is a function, then f(s + t) = f(s) + f(t).
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If x is any real number, then x2 − x.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. tan-1x = sin-1x/cos-1x
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. tan-1(-1) = 3 π/4
> Find the domain of the function. 1 h(x) Vx2 – 5x
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If x > 0 and a > 1, then ln x / ln a = ln x/a.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If x > 0, then (lnx)6 - 6lnx.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If 0 < a < b, then lna < lnb.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. You can always divide by ex.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f is one-to-one, then f-1(x) −1/f(x).
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If f and g are functions, then f 0 g = g 0 f.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. A vertical line intersects the graph of a function at most once.
> Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or give an example that disproves the statement. If x1 < x2 and f is a decreasing function, then f(x1) > f(x2)
> Sketch the graph of the function f(x) = |x2 - 4|x|+ 3|.
> Solve the inequality |x - 1|-|x - 3|≥ 5.
> Solve the equation |2x - 1|-|x + 5|= 3.
> The altitude perpendicular to the hypotenuse of a right triangle is 12 cm. Express the length of the hypotenuse as a function of the perimeter.
> One of the legs of a right triangle has length 4 cm. Express the length of the altitude perpendicular to the hypotenuse as a function of the length of the hypotenuse.
> a. If f0(x) = 1 / 2 - x and fn+1 = f0 0 fn for n = 0, 1, 2, ..., find an expression for fn(x) and use mathematical induction to prove it. b. Graph f0, f1, f2, f3 on the same screen and describe the effects of repeated composition
> If f0(x) = x2 and fn+1(x) − f0(fn(x)) for n = 0, 1, 2, ..., find a formula for fn(x).
> Prove that 1 + 3 + 5 + ∙∙∙ + (2n - 1) = n2.
> Prove that if n is a positive integer, then 7n - 1 is divisible by 6.
> Is it true that f 0 (g + h) = f 0 g + f 0 h?
> A driver sets out on a journey. For the first half of the distance she drives at the leisurely pace of 30 mi/h; she drives the second half at 60 mi/h. What is her average speed on this trip?
> Use indirect reasoning to prove that log25 is an irrational number.
> Find the domain of the function. f(1) = /2t – 1
> Solve the inequality ln(x2 - 2x – 2) ≤ 0.
> a. Show that the function f(x) = ln(x + x2 + 1 ) is an odd function. b. Find the inverse function of f.
> Evaluate (log23)(log34)(log45)∙∙∙(log3132).
> Sketch the region in the plane defined by each of the following equations or inequalities. a. max{x, 2y} = 1 b. -1 ≤ max{x, 2y} ≤ 1 c. max{x, y2} = 1
> The notation max{a, b, ...} means the largest of the numbers a, b, ... . Sketch the graph of each function. a. f(x) = max{x, 1/x} b. f(x) = max{sin x, cos x} c. f(x) = max{x2, 2 + x, 2 - x}
> Sketch the region in the plane consisting of all points (x, y) such that |x - y|+|x|-|y|≤ 2
> Draw the graph of the equation x +|x|= y +|y|.
> Sketch the graph of the function g(x) =|x2 - 1|-|x2 - 4|.
> If f(x) = x2 - 2x + 3, evaluate the difference quotient f (a+h) – f (a) / h
> The graph of g is given. a. State the value of g(2). b. Why is g one-to-one? c. Estimate the value of g-1(2). d. Estimate the domain of g-1. e. Sketch the graph of g-1. 0 1
> Find the domain of the function. 2x – 5 - 5 .3 f(x) x? + x – 6
> Let f be the function whose graph is given. a. Estimate the value of f(2). b. Estimate the values of x such that f(x) = 3. c. State the domain of f. d. State the range of f. e. On what interval is f increasing? f. Is f one-to-one? Explain. g. Is f
> The population of a certain species in a limited environment with initial population 100 and carrying capacity 1000 is P(t) = 100,000/100 + 900e-t where t is measured in years. a. Graph this function and estimate how long it takes for the population to
> The half-life of palladium-100, 100Pd, is four days. (So half of any given quantity of 100Pd will disintegrate in four days.) The initial mass of a sample is one gram. a. Find the mass that remains after 16 days. b. Find the mass m(t) that remains afte
> Solve each equation for x. a. ex = 5 b. lnx = 2 c. eex = 2 d. tan-1x = 1
> Find the exact value of each expression. a. e2ln3 b. log1025 + log104 c. tan(arcsin ½) d. sin(cos-1 (4/5))
> Find the inverse function of f(x) = x + 1 / 2x + 1.
> If f(x) = 2x + lnx, find f -1(2).
> A small-appliance manufacturer finds that it costs $9000 to produce 1000 toaster ovens a week and $12,000 to produce 1500 toaster ovens a week. a. Express the cost as a function of the number of toaster ovens produced, assuming that it is linear. Then s
> Life expectancy improved dramatically in the 20th century. The table gives the life expectancy at birth (in years) of males born in the United States. Use a scatter plot to choose an appropriate type of model. Use your model to predict the life span of a
> Express the function f(x) = 1/ x + x as a composition of three functions.
> Find the domain of the function. x + 4 f(x) x? – 9
> If f(x) = lnx and g(x) = x2 - 9, find the functions a. f 0 g, b. g 0 f, c. f 0 f, d. g 0 g, and their domains.
> Find an expression for the function whose graph consists of the line segment from the point (-2, 2) to the point (-1, 0) together with the top half of the circle with center the origin and radius 1.
> Determine whether f is even, odd, or neither even nor odd. a. f(x) = 2x5 - 3x2 + 2 b. f(x) = x3 - x7 c. f(x) = e-x2 d. f(x) = 1 + sinx
> Use transformations to sketch the graph of the function. if x< 0 f(x) = et – 1 if x> 0
> Use transformations to sketch the graph of the function. f(x) = -cos 2x
> Use transformations to sketch the graph of the function. y = ln(x + 1)
> Use transformations to sketch the graph of the function. y = x2 - 2x + 2
> Use transformations to sketch the graph of the function. y = 2
> Use transformations to sketch the graph of the function. y = (x - 2)3
> The graph of f is given. Draw the graphs of the following functions. a. y = f(x – 8) b. y = -f(x) c. y = 2 – f(x) d. y = 1/2 f(x) - 1 e. y = f -1(x) f. y = f -1(x + 3) yA 1 1
> Evaluate the difference quotient for the given function. Simplify your answer. x + 3 f(x) = x + 1' f(x) – f(1) x - 1
> The graph of a function f is given. a. State the value of f(1). b. Estimate the value of f(-1). c. For what values of x is f(x) − 1? d. Estimate the value of x such that f(x) − 0. e. State the domain and range of f
> Suppose that the graph of f is given. Describe how the graphs of the following functions can be obtained from the graph of f. a. y = f(x) + 8 b. y = f(x + 8) c. y = 1 + 2f(x) d. y = f(x – 2) - 2 e. y = -f(x) f. y = f -1(x)
> Find the domain and range of the function. Write your answer in interval notation. f(t) = 3 + cos 2t
> Find the domain and range of the function. Write your answer in interval notation. h(x) = ln(x + 6)
> Find the domain and range of the function. Write your answer in interval notation. g(x) = 16 −
> Find the domain and range of the function. Write your answer in interval notation. f(x) = 2/(3x – 1)
> Sketch a rough graph of the yield of a crop as a function of the amount of fertilizer used.