Question: Following are four possible transitions for a
Following are four possible transitions for a hydrogen atom
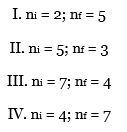
(a) Which transition will emit the shortest - wavelength photon?
(b) For which transition will the atom gain the most energy?
(c) For which transition(s) does the atom lose energy?
> When the principal quantum number is n = 5, how many different values of (a) ℓ and (b) mℓ are possible? (c) How many states have distinct pairs of values of ℓ and mℓ?
> Consider a hydrogen atom and a singly ionized helium atom. Which atom has the lower ground state energy? (a) Hydrogen (b) Helium (c) The ground state energy is the same for both.
> The “size” of the atom in Rutherford’s model is about 1.0 x 10-10 m. (a) Determine the attractive electrostatic force between an electron and a proton separated by this distance. (b) Determine (in eV) the electrostatic potential energy of the atom.
> A transparent oil with index of refraction 1.29 spills on the surface of water (index of refraction 1.33), producing a maximum of reflection with normally incident orange light (wavelength 6.00 x 102 nm in air). Assuming the maximum occurs in the first o
> In a Young’s double - slit experiment, a set of parallel slits with a separation of 0.100 mm is illuminated by light having a wavelength of 589 nm, and the interference pattern is observed on a screen 4.00 m from the slits. (a) What is the difference in
> The wavelengths of the Paschen series for hydrogen are given by 1/λ = RH(1/32 - 1/n2) n = 4, 5, 6, . . . . . (a) Calculate the wavelengths of the first three lines in this series. (b) Identify the region of the electromagnetic spectrum in which these lin
> The wavelengths of the Lyman series for hydrogen are given by 1/λ = RH(1 - 1/n2) n = 2, 3, 4, . . . . . (a) Calculate the wavelengths of the first three lines in this series. (b) Identify the region of the electromagnetic spectrum in which these lines ap
> Suppose the ionization energy of an atom is 4.100 eV. In this same atom, we observe emission lines that have wavelengths of 310.0 nm, 400.0 nm, and 1378 nm. Use this information to construct the energy level diagram with the least number of levels. Assum
> Use Bohr’s model of the hydrogen atom to show that when the atom makes a transition from the state n to the state n - 1, the frequency of the emitted light is given by
> An electron has a de Broglie wavelength equal to the diameter of a hydrogen atom in its ground state. (a) What is the kinetic energy of the electron? (b) How does this energy compare with the magnitude of the ground - state energy of the hydrogen atom?
> A laser used in eye surgery emits a 3.00 - mJ pulse in 1.00 ns, focused to a spot 30.0 μm in diameter on the retina. (a) Find (in SI units) the power per unit area at the retina. (This quantity is called the irradiance.) (b) What energy is delivered per
> As the Earth moves around the Sun, its orbits are quantized. (a) Follow the steps of Bohr’s analysis of the hydrogen atom to show that the allowed radii of the Earth’s orbit are given by where n is an integer quantum
> An electron in chromium moves from the n 5 2 state to the n 5 1 state without emitting a photon. Instead, the excess energy is transferred to an outer electron (one in the n 5 4 state), which is then ejected by the atom. In this Auger (pronounced “ohjay”
> A pulsed ruby laser emits light at 694.3 nm. For a 14.0 - ps pulse containing 3.00 J of energy, find (a) The physical length of the pulse as it travels through space and (b) The number of photons in it. (c) If the beam has a circular cross section 0.600
> (a) How much energy is required to cause an electron in hydrogen to move from the n = 1 state to the n = 2 state? (b) If the electrons gain this energy by collision between hydrogen atoms in a high - temperature gas, find the minimum temperature of the h
> A thin film of glass (n = 1.52) of thickness 0.420 µm is viewed under white light at near normal incidence. What wavelength of visible light is most strongly reflected by the film when surrounded by air?
> In a hydrogen atom, what is the principal quantum number of the electron orbit with a radius closest to 1.0 μm?
> The K series of the discrete spectrum of tungsten contains wavelengths of 0.0185 nm, 0.0209 nm, and 0.0215 nm. The K - shell ionization energy is 69.5 keV. Determine the ionization energies of the L, M, and N shells.
> When an electron drops from the M shell (n = 3) to a vacancy in the K shell (n = 1), the measured wavelength of the emitted x - ray is found to be 0.101 nm. Identify the element.
> A bismuth target is struck by electrons, and x - rays are emitted. Estimate (a) The M - to L - shell transitional energy for bismuth and (b) The wavelength of the x - ray emitted when an electron falls from the M shell to the L shell.
> A tungsten target is struck by electrons that have been accelerated from rest through a 40.0 - kV potential difference. Find the shortest wavelength of the radiation emitted.
> Zirconium (Z = 40) has two electrons in an incomplete d subshell. (a) What are the values of n and ℓ for each electron? (b) What are all possible values of mℓ and ms? (c) What is the electron configuration in the ground state of zirconium?
> Two electrons in the same atom have n = 3 and ℓ = 1. (a) List the quantum numbers for the possible states of the atom. (b) How many states would be possible if the exclusion principle did not apply to the atom?
> A certain element has its outermost electron in a 3p subshell. It has valence +3 because it has three more electrons than a certain noble gas. What element is it?
> (a) Write out the electronic configuration of the ground state for nitrogen (Z = 7). (b) Write out the values for the possible set of quantum numbers n, ℓ, mℓ, and ms for the electrons in nitrogen.
> Apply the Pauli exclusion principle to determine the number of electrons that could occupy the quantum states described by (a) n = 3, ℓ = 2, mℓ = -1 and (b) n = 3, ℓ = 1, and (c) n = 4.
> A thin film of oil (n = 1.25) is located on smooth, wet pavement. When viewed from a direction perpendicular to the pavement, the film reflects most strongly red light at 6.40 x 102 nm and reflects no green light at 512 nm. (a) What is the minimum thickn
> A hydrogen atom is immersed in a magnetic field so that its energy levels split according to the Zeeman effect. Neglecting any effects due to electron spin, how many unique energy levels are available to an electron in the 4f subshell?
> The r - meson has a charge of -e, a spin quantum number of 1, and a mass 1507 times that of the electron. If the electrons in atoms were replaced by ρ - mesons, list the possible sets of quantum numbers for ρ - mesons in the 3d subshell.
> When the principal quantum number is n = 4, how many different values of (a) ℓ and (b) mℓ are possible?
> List the possible sets of quantum numbers for electrons in the 3d subshell.
> For an electron in a 3d state, determine (a) The principle quantum number and (b) The orbital quantum number. (c) How many different magnetic quantum numbers are possible for an electron in that state?
> Hydrogen’s single electron can occupy any of the atom’s distinct quantum states. Determine the number of distinct quantum states in the (a) n = 1, (b) n = 2, and (c) n = 3 energy levels.
> Using the concept of standing waves, de Broglie was able to derive Bohr’s stationary orbit postulate. He assumed a confined electron could exist only in states where its de Broglie waves form standing wave patterns, as in Figure 28.6. C
> A general expression for the energy levels of one – electron atoms and ions is Here μ is the reduced mass of the atom, given by μ = m1m2 / (m1 + m2), where m1 is the mass of the electron and m2 is the mass of
> Consider a Bohr model of doubly ionized lithium. (a) Write an expression similar to Equation 28.14 for the energy levels of the sole remaining electron. (b) Find the energy corresponding to n = 4. (c) Find the energy corresponding to n = 2. (d) Calculate
> The orbital radii of a hydrogen - like atom is given by the equation rn = n2ħ2/Zmekee2 What is the radius of the first Bohr orbit in (a) He+, (b) Li2+, and (c) Be3+?
> A thin layer of liquid methylene iodide (n = 1.756) is sandwiched between two flat, parallel plates of glass (n = 1.50). What is the minimum thickness of the liquid layer if normally incident light with λ = 6.00 x 102 nm in air is to be strongly reflecte
> (a) Write an expression relating the kinetic energy KE of the electron and the potential energy PE in the Bohr model of the hydrogen atom. (b) Suppose a hydrogen atom absorbs a photon of energy E, resulting in the transfer of the electron to a higher - e
> An electron is in the second excited orbit of hydrogen, corresponding to n = 3. Find (a) The radius of the orbit and (b) The wavelength of the electron in this orbit.
> (a) Calculate the angular momentum of the Moon due to its orbital motion about Earth. In your calculation use 3.84 x 108 m as the average Earth–Moon distance and 2.36 x 106 s as the period of the Moon in its orbit. (b) If the angular momentum of the Moon
> A photon with energy 2.28 eV is absorbed by a hydrogen atom. Find (a) The minimum n for a hydrogen atom that can be ionized by such a photon and (b) The speed of the electron released from the state in part (a) when it is far from the nucleus.
> Consider a large number of hydrogen atoms, with electrons all initially in the n = 4 state. (a) How many different wavelengths would be observed in the emission spectrum of these atoms? (b) What is the longest wavelength that could be observed? (c) To wh
> (a) If an electron makes a transition from the n = 4 Bohr orbit to the n = 2 orbit, determine the wavelength of the photon created in the process. (b) Assuming that the atom was initially at rest, determine the recoil speed of the hydrogen atom when this
> A particle of charge q and mass m, moving with a constant speed v, perpendicular to a constant magnetic field B, follows a circular path. If in this case the angular momentum about the center of this circle is quantized so that mvr = 2nħ, show
> The Balmer series for the hydrogen atom corresponds to electronic transitions that terminate in the state with quantum number n = 2 as shown in Figure P28.19. Consider the photon of longest wavelength corresponding to a transition shown in the figure. De
> A hydrogen atom initially in its ground state (n = 1) absorbs a photon and ends up in the state for which n = 3. (a) What is the energy of the absorbed photon? (b) If the atom eventually returns to the ground state, what photon energies could the atom em
> What is the energy of a photon that, when absorbed by a hydrogen atom, could cause an electronic transition from (a) The n = 2 state to the n = 5 state and (b) The n = 4 state to the n = 6 state?
> A soap bubble (n = 1.33) having a wall thickness of 120 nm is floating in air. (a) What is the wavelength of the visible light that is most strongly reflected? (b) Explain how a bubble of different thickness could also strongly reflect light of this same
> A hydrogen atom emits a photon of wavelength 656 nm. From what energy orbit to what lower - energy orbit did the electron jump?
> A photon is emitted when a hydrogen atom undergoes a transition from the n = 5 state to the n = 3 state. Calculate (a) The wavelength, (b) The frequency, and (c) The energy (in eV) of the emitted photon.
> Show that the speed of the electron in the nth Bohr orbit in hydrogen is given by
> For a hydrogen atom in its ground state, use the Bohr model to compute (a) The orbital speed of the electron, (b) The kinetic energy of the electron, and (c) The electrical potential energy of the atom.
> A hydrogen atom is in its first excited state (n = 2). Using the Bohr theory of the atom, calculate (a) The radius of the orbit, (b) The linear momentum of the electron, (c) The angular momentum of the electron, (d) The kinetic energy, (e) The potential
> What is the (a) Energy in eV and (b) Wavelength in μm of a photon that, when absorbed by a hydrogen atom, could cause a transition from the n = 3 to the n = 6 energy level?
> Singly ionized helium (He+) is a hydrogen - like atom. Determine the energy in eV required to raise a He+ electron from the n = 1 to the n = 2 energy level.
> Determine the energies in eV of the (a) Second and (b) Third energy levels of the hydrogen atom. Calculate the orbital radius in nm of an electron in hydrogen’s (c) Second and (d) Third energy levels.
> The so - called Lyman - α photon is the lowest energy photon in the Lyman series of hydrogen and results from an electron transitioning from the n = 2 to the n = 1 energy level. Determine (a) The energy in eV and (b) The wavelength in nm of a Lyman - α p
> Waves from a radio station have a wavelength of 3.00 x 102 m. They travel by two paths to a home receiver 20.0 km from the transmitter. One path is a direct path, and the second is by reflection from a mountain directly behind the home receiver. What is
> In a Rutherford scattering experiment, an α - particle (charge = +2e) heads directly toward a gold nucleus (charge = +79e). The α - particle had a kinetic energy of 5.0 MeV when very far (r ( ∞) from the nucleus. Assuming the gold nucleus to be fixed in
> The “size” of the atom in Rutherford’s model is about 1.0 x 10-10 m. (a) Determine the speed of an electron moving about the proton using the attractive electrostatic force between an electron and a proton separated by this distance. (b) Does this speed
> An isolated atom of a certain element emits light of wavelength 520. nm when the atom falls from its fifth excited state into its second excited state. The atom emits a photon of wavelength 410. nm when it drops from its sixth excited state into its seco
> Does the light emitted by a neon sign constitute a continuous spectrum or only a few colors? Defend your answer.
> The ionization energies for Li, Na, K, Rb, and Cs are 5.390, 5.138, 4.339, 4.176, and 3.893 eV, respectively. Explain why these values are to be expected in terms of the atomic structures.
> List some ways in which quantum mechanics altered our view of the atom pictured by the Bohr theory.
> Can the electron in the ground state of hydrogen absorb a photon of energy less than 13.6 eV? Can it absorb a photon of energy greater than 13.6 eV? Explain.
> Why are three quantum numbers needed to describe the state of a one - electron atom (ignoring spin)?
> Suppose the electron in the hydrogen atom obeyed classical mechanics rather than quantum mechanics. Why should such a hypothetical atom emit a continuous spectrum rather than the observed line spectrum?
> An energy of about 21 eV is required to excite an electron in a helium atom from the 1s state to the 2s state. The same transition for the He+ ion requires approximately twice as much energy. Explain.
> Monochromatic light of wavelength λ is incident on a pair of slits separated by 2.40 x 10-4 m, and forms an interference pattern on a screen placed 1.80 m away from the slits. The first - order bright fringe is 4.52 mm from the center of the central maxi
> A nonrelativistic electron and a nonrelativistic proton are moving and have the same de Broglie wavelength. Which of the following are also the same for the two particles? (a) Speed (b) Kinetic energy (c) Momentum (d) Frequency
> True or False: As the momentum of a particle of mass m increases, its wavelength increases.
> A photon of energy E0 strikes a free electron, with the scattered photon of energy E moving in the direction opposite that of the incident photon. In this Compton effect interaction, what is the resulting kinetic energy of the electron? (a) E0 (b) E (c)
> An x - ray photon is scattered by an electron. Does the frequency of the scattered photon relative to that of the incident photon (a) Increase, (b) Decrease, or (c) Remain the same?
> True or False: When a photon scatters off an electron, the photon loses energy.
> (a) What is the surface temperature of Betelgeuse, a red giant star in the constellation of Orion, which radiates with a peak wavelength of about 970 nm? (b) Rigel, a bluish - white star in Orion, radiates with a peak wavelength of 145 nm. Find the tempe
> From the scattering of sunlight, J. J. Thomson calculated the classical radius of the electron as having the value 2.82 x 10-15 m. Sunlight with an intensity of 5.00 x 102 W/ m2 falls on a disk with this radius. Assume light is a classical wave and the l
> How fast must an electron be moving if all its kinetic energy is lost to a single x - ray photon (a) At the high end of the x - ray electromagnetic spectrum with a wavelength of 1.00 x 10-8 m and (b) At the low end of the x - ray electromagnetic spectrum
> Red light of wavelength 670. nm produces photoelectrons from a certain photoemissive material. Green light of wavelength 520. nm produces photoelectrons from the same material with 1.50 times the maximum kinetic energy. What is the material’s work functi
> A light source of wavelength λ illuminates a metal and ejects photoelectrons with a maximum kinetic energy of 1.00 eV. A second light source of wavelength λ /2 ejects photoelectrons with a maximum kinetic energy of 4.00 eV. What is the work function of t
> Radio waves from a star, of wavelength 2.50 x 102 m, reach a radio telescope by two separate paths, as shown in Figure P24.13. One is a direct path to the receiver, which is situated on the edge of a cliff by the ocean. The second is by reflection off th
> An electron initially at rest recoils after a head - on collision with a 6.20 - keV photon. Determine the kinetic energy acquired by the electron.
> Photons of wavelength 4.50 x 102 nm are incident on a metal. The most energetic electrons ejected from the metal are bent into a circular arc of radius 20.0 cm by a magnetic field with a magnitude of 2.00 x 10-5 T. What is the work function of the metal?
> Johnny Jumper’s favorite trick is to step out of his 16th - story window and fall 50.0 m into a pool. A news reporter takes a picture of 75.0 - kg Johnny just before he makes a splash, using an exposure time of 5.00 ms. Find (a) Johnny’s de Broglie wavel
> Figure P27.45 shows the spectrum of light emitted by a firefly. (a) Determine the temperature of a blackbody that would emit radiation peaked at the same frequency. (b) Based on your result, explain whether firefly radiation is blackbody radiation. Figu
> An x - ray tube is operated at 5.00 x 104 V. (a) Find the minimum wavelength of the radiation emitted by this tube. (b) If the radiation is directed at a crystal, the first - order maximum in the reflected radiation occurs when the grazing angle is 2.5°.
> A 2.0 - kg object falls from a height of 5.0 m to the ground. If the change in the object’s kinetic energy could be converted to visible light of wavelength 5.0 x 10-7 m, how many photons would be produced?
> Find the speed of an electron having a de Broglie wavelength equal to its Compton wavelength.
> A microwave photon in the x - band region has a wavelength of 3.00 cm. Find (a) The momentum, (b) The frequency, and (c) The energy of the photon in electron volts.
> (a) Show that the kinetic energy of a nonrelativistic particle can be written in terms of its momentum as KE = p2/2m. (b) Use the results of part (a) to find the minimum kinetic energy of a proton confined within a nucleus having a diameter of 1.0 x 10-1
> The average lifetime of a muon is about 2 μs. Estimate the minimum uncertainty in the energy of a muon.
> A student sets up a double - slit experiment using monochromatic light of wavelength λ. The distance between the slits is equal to 25 λ. (a) Find the angles at which the m = 1, 2, and 3 maxima occur on the viewing screen. (b) At what angles do the first
> In a nonrelativistic experiment, an electron and a proton are each located along the x - axis to within an uncertainty of 2.50 μm. Determine the minimum uncertainty in the x - component of the velocity of (a) The electron, and (b) The proton.
> An electron and a 0.0200 - kg bullet each have a velocity of magnitude 5.00 x 102 m/s, accurate to within 0.0100%. Within what lower limit could we determine the position of each object along the direction of the velocity?
> An electron is located on a pinpoint having a diameter of 2.5 μm. What is the minimum uncertainty in the speed of the electron?
> In the ground state of hydrogen, the uncertainty in the position of the electron is roughly 0.10 nm. If the speed of the electron is approximately the same as the uncertainty in its speed, about how fast is it moving?
> A nonrelativistic particle of mass m and charge q is accelerated from rest through a potential difference ΔV. (a) Use conservation of energy to find a symbolic expression for the momentum of the particle in terms of m, q, and ΔV. (b) Write a symbolic exp
> The resolving power of a microscope is proportional to the wavelength used. A resolution of 1.0 x 10-11 m (0.010 nm) would be required in order to “see” an atom. (a) If electrons were used (electron microscope), what minimum kinetic energy would be requi
> An electron and a 6.00 - kg bowling ball each have 4.50 eV of kinetic energy. Calculate (a) λe and (b) λb, the de Broglie wavelengths of the electron and the bowling ball, respectively. (c) Calculate the wavelength λp of a 4.50 - eV photon.
> De Broglie postulated that the relationship λ = h/p is valid for relativistic particles. What is the de Broglie wavelength for a (relativistic) electron having a kinetic energy of 3.00 MeV?

