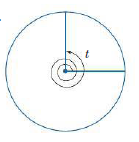
Question: Give the radian measure of each angle
> Find t such that -π>2 ≤ t ≤ π>2 and t satisfies the stated condition. sin t = -cos t
> Find t such that -π>2 ≤ t ≤ π>2 and t satisfies the stated condition. sin t = cos t
> Refer to Exercise 27. Let g (p1, p2) be the number of people who will take the train when p1 is the price of the bus ride and p2 is the price of the train ride. Would you expect ∂g/∂p1 to be positive or negative? How about ∂g/∂p2? Exercise 27: In a cert
> Find t such that -π>2 ≤ t ≤ π>2 and t satisfies the stated condition. sin t = -sin(-π>3)
> Find t such that -π>2 ≤ t ≤ π>2 and t satisfies the stated condition. sin t = -sin(π>6)
> Find t such that -π>2 ≤ t ≤ π>2 and t satisfies the stated condition. sin t = -sin(3π>8)
> Find t such that -π>2 ≤ t ≤ π>2 and t satisfies the stated condition. sin t = sin(-4π>3)
> Find t such that -π>2 ≤ t ≤ π>2 and t satisfies the stated condition. sin t = sin(7π>6)
> Find t such that -π>2 ≤ t ≤ π>2 and t satisfies the stated condition. sin t = sin(3π>4)
> Find t such that 0 ≤ t ≤ π and t satisfies the stated condition. cos t = cos(-3π/4)
> Find t such that 0 ≤ t ≤ π and t satisfies the stated condition. cos t = cos(-5π/8)
> Find t such that 0 ≤ t ≤ π and t satisfies the stated condition. cos t = cos(-4π/6)
> Find t such that 0 ≤ t ≤ π and t satisfies the stated condition. cos t = cos(5π/4)
> In a certain suburban community, commuters have the choice of getting into the city by bus or train. The demand for these modes of transportation varies with their cost. Let f (p1, p2) be the number of people who will take the bus when p1 is the price of
> Find t such that 0 ≤ t ≤ π and t satisfies the stated condition. cos t = cos(3π/2)
> Find t such that 0 ≤ t ≤ π and t satisfies the stated condition. cos t = cos(-π>/6)
> Refer to various right triangles whose sides and angles are labeled as in Fig. 16. Round off all lengths of sides to one decimal place. If t = 1.1 and b = 3.5, find a and c. Figure 16: t a b
> Refer to various right triangles whose sides and angles are labeled as in Fig. 16. Round off all lengths of sides to one decimal place. If t = .5 and a = 2.4, find b and c. Figure 16: t a b
> Refer to various right triangles whose sides and angles are labeled as in Fig. 16. Round off all lengths of sides to one decimal place. If t = .9 and c = 20.0, find a and b. Figure 16: t a b
> Refer to various right triangles whose sides and angles are labeled as in Fig. 16. Round off all lengths of sides to one decimal place. If t = .4 and a = 10.0, find c. Figure 16: t a b
> Refer to various right triangles whose sides and angles are labeled as in Fig. 16. Round off all lengths of sides to one decimal place. If t = .4 and c = 5.0, find a. Figure 16: t a b
> Refer to various right triangles whose sides and angles are labeled as in Fig. 16. Round off all lengths of sides to one decimal place. If t = 1.1 and b = 3.2, find c. Figure 16: t a b
> Refer to various right triangles whose sides and angles are labeled as in Fig. 16. Round off all lengths of sides to one decimal place. If t = 1.1 and c = 10.0, find b. Figure 16: t a b
> Refer to various right triangles whose sides and angles are labeled as in Fig. 16. Round off all lengths of sides to one decimal place. Estimate t if a = 12, b = 5, and c = 13. Figure 16: t a b
> Match the graph of the function to the systems of level curves shown in Figs. 8(a)–(d). Figure 8: 2 2= ex² + e-4y² 2 e (b) 2₂x0 몸 라 (d) 2.
> Give the values of sin t and cos t, where t is the radian measure of the angle shown. t (.8, -.6)
> Give the values of sin t and cos t, where t is the radian measure of the angle shown. (-.6, -.8)
> Give the values of sin t and cos t, where t is the radian measure of the angle shown. (.6, .8)
> Give the values of sin t and cos t, where t is the radian measure of the angle shown. (-2, 2)
> Give the values of sin t and cos t, where t is the radian measure of the angle shown. (2, -3)
> Give the values of sin t and cos t, where t is the radian measure of the angle shown. (-2, 1)
> Give the values of sin t and cos t, where t is the radian measure of the angle shown. t 3 5
> Give the values of sin t and cos t, where t is the radian measure of the angle shown. 13, t 12
> Convert the following to radian measure. 990˚ , - 270˚ , - 540˚
> Convert the following to radian measure. 450˚ , -210˚ , -90˚
> Match the graph of the function to the systems of level curves shown in Figs. 8(a)–(d). Figure 8: NY 2 15x²y²e-2². x² + y² 150 107 e (b) 2₂x0 몸 라 (d) 2.
> Convert the following to radian measure. 18 ˚, 72˚ , 150 ˚
> Convert the following to radian measure. 30 ˚, 120˚, 315˚
> Construct angles with the following radian measure. 2π/3, - π/6, 7π/2
> Construct angles with the following radian measure. π/6, - 2π/3, - π
> Construct angles with the following radian measure. - π/4, - 3π/2, - 3π
> Construct angles with the following radian measure. - π/3, - 3π/4, - 7π/2
> Construct angles with the following radian measure. π/3, 5π/2, 6π
> Construct angles with the following radian measure. 3π/2, 3π/4, 5π
> Give the radian measure of each angle described.
> Give the radian measure of each angle described. 0
> Match the graph of the function to the systems of level curves shown in Figs. 8(a)–(d). Figure 8: x 2 z = x² - x² - y² 2 e (b) 2₂x0 몸 라 (d) 2.
> Give the radian measure of each angle described.
> Give the radian measure of each angle described.
> Give the radian measure of each angle described.
> Give the radian measure of each angle described.
> Give the radian measure of each angle described.
> Let f (x, y, λ) = xy + λ (5 - x - y). Find f (1, 2, 3).
> If A dollars are deposited in a bank at a 6% continuous interest rate, the amount in the account after t years is f (A, t) = Ae0.06t. Find and interpret f (10, 11.5).
> Let f (x, y, z) = x2ey/z. Compute f (-1, 0, 1), f (1, 3, 3), and f (5, -2, 2).
> Let f (x, y) = x√y/(1 + x). Compute f (2, 9), f (5, 1), and f (0, 0).
> Match the graph of the function to the systems of level curves shown in Figs. 8(a)–(d). Figure 8: 2 -4 1 + x² + 2y² 2 e (b) 2₂x0 몸 라 (d) 2.
> The present value of y dollars after x years at 15% continuous interest is f (x, y) = ye-0.15x. Sketch some sample level curves. (Economists call this collection of level curves a discount system.)
> Let R be the rectangle consisting of all points (x, y), such that 0 ≤ x ≤ 4, 1 ≤ y ≤ 3, and calculate the double integral. ∫R∫ 5 dx dy
> Let R be the rectangle consisting of all points (x, y), such that 0 ≤ x ≤ 4, 1 ≤ y ≤ 3, and calculate the double integral. ∫R∫ (2x + 3y) dx dy
> Calculate the iterated integral. ∫05 (∫14 (2xy4 + 3) dy) dx
> Calculate the iterated integral. ∫01 (∫04 (x√y + y) dy) dx
> Find the straight line that best fits the following data points, where “best” is meant in the sense of least squares. (0, 1), (1, -1), (2, -3), (3, -5)
> Find the straight line that best fits the following data points, where “best” is meant in the sense of least squares. (1, 1), (3, 4), (5, 7)
> Find the straight line that best fits the following data points, where “best” is meant in the sense of least squares. (1, 1), (2, 3), (3, 6)
> The solution to Exercise 29 is x = 10, y = 20, λ = 10. If 1 additional foot of fencing becomes available, compute the new optimal dimensions and the new area. Show that the increase in area (compared with the area in Exercise 29) is approxim
> A person wants to plant a rectangular garden along one side of a house and put a fence on the other three sides. (See Fig. 1.) Using the method of Lagrange multipliers, find the dimensions of the garden of greatest area that can be enclosed with 40 feet
> A certain production process uses units of labor and capital. If the quantities of these commodities are x and y, respectively, the total cost is 100x + 200y dollars. Draw the level curves of height 600, 800, and 1000 for this function. Explain the signi
> Find the dimensions of a rectangular box of volume 1000 cubic inches for which the sum of the dimensions is minimized.
> Use the method of Lagrange multipliers to: Find the values of x, y, z that minimize 3x2 + 2y2 + z2 + 4x + y + 3z, subject to the constraint 4 - x - y - z = 0.
> Use the method of Lagrange multipliers to: Find the values of x, y that minimize -x2 - 3xy – ½ y2 + y + 10, subject to the constraint 10 - x - y = 0.
> Use the method of Lagrange multipliers to: Maximize 3x2 + 2xy - y2, subject to the constraint 5 - 2x - y = 0.
> Find the values of x, y, z at which f (x, y, z) = x2 + 4y2 + 5z2 - 6x + 8y + 3 assumes its minimum value.
> Find all points (x, y) where f (x, y) has a possible relative maximum or minimum. Then, use the second-derivative test to determine, if possible, the nature of f (x, y) at each of these points. If the second-derivative test is inconclusive, so state. f (
> Find all points (x, y) where f (x, y) has a possible relative maximum or minimum. Then, use the second-derivative test to determine, if possible, the nature of f (x, y) at each of these points. If the second-derivative test is inconclusive, so state. f (
> Find all points (x, y) where f (x, y) has a possible relative maximum or minimum. Then, use the second-derivative test to determine, if possible, the nature of f (x, y) at each of these points. If the second-derivative test is inconclusive, so state. f (
> Find all points (x, y) where f (x, y) has a possible relative maximum or minimum. f (x, y) = ½ x2 + 4xy + y3 + 8y2 + 3x + 2
> Find all points (x, y) where f (x, y) has a possible relative maximum or minimum. f (x, y) = x3 + 3x2 + 3y2 - 6y + 7
> Suppose that a topographic map is viewed as the graph of a certain function f (x, y). What are the level curves?
> Find all points (x, y) where f (x, y) has a possible relative maximum or minimum. f (x, y) = x2 + 3xy - y2 - x - 8y + 4
> Find all points (x, y) where f (x, y) has a possible relative maximum or minimum. f (x, y) = -x2 + 2y2 + 6x - 8y + 5
> The crime rate in a certain city can be approximated by a function f (x, y, z), where x is the unemployment rate, y is the number of social services available, and z is the size of the police force. Explain why ∂f/∂x > 0, ∂f/∂y < 0, and ∂f/∂z < 0.
> A dealer in a certain brand of electronic calculator finds that (within certain limits) the number of calculators she can sell per week is given by f (p, t) = - p + 6t - .02 pt, where p is the price of the calculator and t is the number of dollars spent
> Let f (x, y) = 2x3 + x2y - y2. Compute ∂2f/∂x2, ∂2f/∂y2 and ∂2f/∂x∂y (x, y) = (1, 2).
> Let f (x, y) = x5 - 2 x3y + ½ y4. Find ∂2f/∂x2, ∂2f/∂y2, ∂2f/∂x∂y, and ∂2f/∂y∂x.
> Let f (x, y, z) = (x + y) z. Evaluate ∂f/∂y at (x, y, z) = (2, 3, 4).
> Let f (x, y) = x3y + 8. Compute ∂f/∂x (1, 2) and ∂f/∂y (1, 2).
> Let f (x, y, λ) = xy + λ(5 - x - y). Find ∂f/∂x, ∂f/∂y and ∂f/∂λ.
> Let f (x, y, z) = x3 - yz2. Find ∂f/∂x, ∂f/∂y and ∂f/∂z.
> Find a function f (x, y) that has the curve y = 2/x2 as a level curve.
> Let g (x, y) = √(x2 + 2y2). Compute g (1, 1), g (0,-1), and g (a, b).
> Let f (x, y) = x/(x - 2y). Find ∂f/∂x and ∂f/∂y.
> Let f (x, y) = ex/y. Find ∂f/∂x and ∂f/∂y.
> Let f (x, y) = 3x – ½ y4 + 1. Find ∂f/∂x and ∂f/∂y.
> Let f (x, y) = 3x2 + xy + 5y2. Find ∂f/∂x and ∂f/∂y.
> What expression involving a partial derivative gives an approximation to f (a + h, b) - f (a, b)?
> Explain how to find a second partial derivative of a function of two variables.
> Explain how to find a first partial derivative of a function of two variables.
> Give an example of a level curve of a function of two variables.
> Give a formula for evaluating a double integral in terms of an iterated integral.