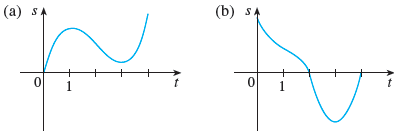
Question: Graphs of the position functions of two
Graphs of the position functions of two particles are shown, where t is measured in seconds. When is each particle speeding up? When is it slowing down? Explain.
Transcribed Image Text:
(a) SA (b) SA 1
> The velocity graph of a car accelerating from rest to a speed of 120 km/h over a period of 30 seconds is shown. Estimate the distance traveled during this period. םע (km/h) 80 40 20 30 (seconds) 10
> The velocity graph of a braking car is shown. Use it to estimate the distance traveled by the car while the brakes are applied. (ft/s) 60 40 20 6 (seconds) 4 t 2.
> Dinosaur fossils are too old to be reliably dated using carbon-14. (See Exercise 11.) Suppose we had a 68-millionyear- old dinosaur fossil. What fraction of the living dinosaur’s 14C would be remaining today? Suppose the minimum detectable amount is 0.1%
> When we estimate distances from velocity data, it is sometimes necessary to use times t0, t1, t2, t3, . . . that are not equally spaced. We can still estimate distances using the time periods Δti = ti - ti-1. For example, on May 7, 1992, the
> Oil leaked from a tank at a rate of r(t) liters per hour. The rate decreased as time passed and values of the rate at two-hour time intervals are shown in the table. Find lower and upper estimates for the total amount of oil that leaked out. t (h) 2
> The table shows speedometer readings at 10-second intervals during a 1-minute period for a car racing at the Daytona International Speedway in Florida. (a) Estimate the distance the race car traveled during this time period using the velocities at the be
> The speed of a runner increased steadily during the first three seconds of a race. Her speed at half-second intervals is given in the table. Find lower and upper estimates for the distance that she traveled during these three seconds. t (s) 0.5 1.0
> (a) If f (x) = ln x, 1 ≤ x ≤ 4, use the commands discussed in Exercise 11 to find the left and right sums for n = 10, 30, and 50. (b) Illustrate by graphing the rectangles in part (a). (c) Show that the exact area under f lies between 2.50 and 2.59. Exe
> Some computer algebra systems have commands that will draw approximating rectangles and evaluate the sums of their areas, at least if xi* is a left or right endpoint. (For instance, in Maple use leftbox, rightbox, leftsum, and rightsum.) (a) If f (x) = 1
> With a programmable calculator (or a computer), it is possible to evaluate the expressions for the sums of areas of approximating rectangles, even for large values of n, using looping. (On a TI use the Is. command or a For-EndFor loop, on a Casio use Isz
> Find the point at which the line intersects the given plane. 5x = y/2 = z + 2; 10x - 7y + 3z + 24 = 0
> With a programmable calculator (or a computer), it is possible to evaluate the expressions for the sums of areas of approximating rectangles, even for large values of n, using looping. (On a TI use the Is. command or a For-EndFor loop, on a Casio use Isz
> Evaluate the upper and lower sums for f (x) = 1 + x2, -1 ≤ x ≤ 1, with n = 3 and 4. Illustrate with diagrams like Figure 14. Figure 14: y. a b
> For any vectors u and v in V3, |u × v | − |v × u |.
> Scientists can determine the age of ancient objects by the method of radiocarbon dating. The bombardment of the upper atmosphere by cosmic rays converts nitrogen to a radioactive isotope of carbon, 14C, with a half-life of about 5730 years. Vegetation ab
> Find dy/dx by implicit differentiation. cos(xy) = 1 + sin y
> Copy the vectors in the figure and use them to draw the following vectors. (a). u + v (b). u + w (c) v + w (d). u - v (e). v + u + w (f). - w - v V
> What are the projections of the point (2, 3, 5) on the xy-, yz-, and xz-planes? Draw a rectangular box with the origin and (2, 3, 5) as opposite vertices and with its faces parallel to the coordinate planes. Label all vertices of the box. Find the length
> Name all the equal vectors in the parallelogram shown. A B E D C.
> Sketch the points (1, 5, 3), (0, 2, -3), (-3, 0, 2), and (2, -2, -1) on a single set of coordinate axes.
> Find the cross product a × b and verify that it is orthogonal to both a and b. a = 2, 3, 0 , b = 1, 0,5
> Differentiate. y = x / 2 - tan x
> Find two unit vectors that are orthogonal to both j + 2k and i - 2j + 3k.
> A surface consists of all points P such that the distance from P to the plane y = 1 is twice the distance from P to the point (0, -1, 0). Find an equation for this surface and identify it.
> Identify and sketch the graph of each surface. x = y2 + z2 - 2y - 4z + 5
> A sample of tritium-3 decayed to 94.5% of its original amount after a year. (a) What is the half-life of tritium-3? (b) How long would it take the sample to decay to 20% of its original amount?
> Identify and sketch the graph of each surface. 4x2 + 4y2 - 8y + z2 = 0
> Identify and sketch the graph of each surface. y2 + z2 = 1 + x2
> Identify and sketch the graph of each surface. -4x2 + y2 - 4z2 = 4
> Identify and sketch the graph of each surface. 4x - y + 2z = 4
> Find a vector equation and parametric equations for the line. The line through the point (2, 2.4, 3.5) and parallel to the vector 3i + 2j - k
> Identify and sketch the graph of each surface. x2 = y2 + 4z2
> Identify and sketch the graph of each surface. y = z2
> If u and v are the vectors shown in the figure, find u ∙ v and |u × v |. Is u × v directed into the page or out of it? |v| = 3 45° |u|=2
> Identify and sketch the graph of each surface. x = z
> Identify and sketch the graph of each surface. x = 3
> Find the distance between the planes 3x + y - 4z = 2 and 3x + y - 4z = 24.
> The half-life of cesium-137 is 30 years. Suppose we have a 100-mg sample. (a) Find the mass that remains after t years. (b) How much of the sample remains after 100 years? (c) After how long will only 1 mg remain?
> (a). Show that the planes x + y - z = 1 and 2x - 3y + 4z = 5 are neither parallel nor perpendicular. (b). Find, correct to the nearest degree, the angle between these planes.
> Copy the vectors in the figure and use them to draw each of the following vectors. (a). a + b (b). a - b (c). 1 2 a (d). 2a + b a b
> Find an equation of the plane. The plane through (2, 1, 0) and parallel to x + 4y - 3z = 1
> Find an equation of the plane. The plane through the point (1, 1 2 , 1 3 ) and parallel to the plane x + y + z = 0
> Find parametric equations for the line. The line through (-2, 2, 4) and perpendicular to the plane 2x - y + 5z = 12
> Find parametric equations for the line. The line through (1, 0, -1) and parallel to the line 1 3 (x – 4) = 1 2 y = z + 2
> Find parametric equations for the line. The line through (4, -1, 2) and (1, 1, 5)
> Find the magnitude of the torque about P if a 50-N force is applied as shown. 50 N 30° 40 cm P
> A constant force F = 3i + 5j + 10k moves an object along the line segment from (1, 0, 2) to (5, 3, 8). Find the work done if the distance is measured in meters and the force in newtons.
> (a). Find a vector perpendicular to the plane through the points A (1, 0, 0), B (2, 0, -1), and C (1, 4, 3). (b). Find the area of triangle ABC.
> Given the points A (1, 0, 1), B (2, 3, 0), C (-1, 1, 4), and D (0, 3, 2), find the volume of the parallelepiped with adjacent edges AB, AC, and AD.
> Describe and sketch the surface. z = sin y
> Describe and sketch the surface. xy = 1
> Find an equation of the plane. The plane through the point (1, -1, -1) and parallel to the plane 5x - y - z = 6
> Describe and sketch the surface. y = z2
> Graph the surfaces z = x2 + y2 and z = 1 - y2 on a common screen using the domain |x | < 1.2, |y | < 1.2 and observe the curve of intersection of these surfaces. Show that the projection of this curve onto the xy-plane is an ellipse.
> Describe and sketch the surface. z = 1 - y2
> Sketch the region bounded by the paraboloids z = x2 + y2 and z = 2 - x2 - y2.
> Use a computer with three-dimensional graphing software to graph the surface. Experiment with viewpoints and with domains for the variables until you get a good view of the surface. x2 - 6x + 4y2 – z = 0
> Use a computer with three-dimensional graphing software to graph the surface. Experiment with viewpoints and with domains for the variables until you get a good view of the surface. -4x2 - y2 + z2 = 0
> Use a computer with three-dimensional graphing software to graph the surface. Experiment with viewpoints and with domains for the variables until you get a good view of the surface. x2 - y2 - z = 0
> Graphs of the velocity functions of two particles are shown, where t is measured in seconds. When is each particle speeding up? When is it slowing down? Explain. (a) V수 (b) V수 이1 1 1
> Describe and sketch the surface. 4x2 + y2 = 4
> Determine whether the lines L1 and L2 are parallel, skew, or intersecting. If they intersect, find the point of intersection. L1: x = 5 - 12t, y = 3 + 9t, z = 1 - 3t L2: x = 3 + 8s, y = -6s, z = 7 + 2s
> Reduce the equation to one of the standard forms, classify the surface, and sketch it. 4x2 + y2 + z2 - 24x - 8y + 4z + 55 = 0
> Reduce the equation to one of the standard forms, classify the surface, and sketch it. x2 - y2 + z2 - 4x - 2z = 0
> Reduce the equation to one of the standard forms, classify the surface, and sketch it. y2 = x2 + 4z2 + 4
> Reduce the equation to one of the standard forms, classify the surface, and sketch it. x2 + 2y2 2z2 = 0
> Reduce the equation to one of the standard forms, classify the surface, and sketch it. 4x2 - y + 2z2 = 0
> Reduce the equation to one of the standard forms, classify the surface, and sketch it. y² = x² + §z²
> Describe and sketch the surface. x2 + z2 = 1
> Match the equation with its graph (labeled I–VIII). Give reasons for your choice. x2 + 2z2 = 1 ZA y х.
> A particle moves according to a law of motion s = f(t), t ≥ 0, where t is measured in seconds and s in feet. (a) Find the velocity at time t. (b) What is the velocity after 1 second? (c) When is the particle at rest? (d) When is the part
> Find a vector equation and parametric equations for the line. The line through the point (6, -5, 2) and parallel to the vector 1, 3, − 2 3
> Match the equation with its graph (labeled I–VIII). Give reasons for your choice. y2 = x2 + 2z2 ZA y
> Match the equation with its graph (labeled I–VIII). Give reasons for your choice. 2x2 + y2 - z2 = 1 ZA y XA
> Match the equation with its graph (labeled I–VIII). Give reasons for your choice. x2 - y2 + z2 = 1 ZA y X.
> Match the equation with its graph (labeled I–VIII). Give reasons for your choice. 9x2 + 4y2 + z2 = 1 ZA y
> Match the equation with its graph (labeled I–VIII). Give reasons for your choice. x2 + 4y2 + 9z2 = 1 ZA y
> Use traces to sketch and identify the surface. y² 1 9 25 4. + +
> Find parametric equations and symmetric equations for the line. The line through the points (1, 2.4, 4.6) and (2.6, 1.2, 0.3)
> Find the distance between the given parallel planes. 2x - 3y + z = 4, 4x - 6y + 2z = 3
> Find the distance from the point to the given plane. (-6, 3, 5), x - 2y - 4z = 8
> Find the distance from the point to the given plane. (1, -2, 4), 3x + 2y + 6z = 5
> (a). Find symmetric equations for the line that passes through the point (1, -5, 6) and is parallel to the vector −1, 2, −3 . (b). Find the points in which the required line in part (a) intersects the coordinate planes.
> A particle moves according to a law of motion s = f(t), t ≥ 0, where t is measured in seconds and s in feet. (a) Find the velocity at time t. (b) What is the velocity after 1 second? (c) When is the particle at rest? (d) When is the part
> Use the formula in Exercise 12.4.45 to find the distance from the point to the given line. (0, 1, 3); x = 2t, y = 6 - 2t, z = 3 + t Exercise 12.4.45: x b| |a| Ja x b| |a X d =
> Find parametric equations and symmetric equations for the line. The line through the points (0, 1 2 , 1) and (2, 1, -3)
> Use the formula in Exercise 12.4.45 to find the distance from the point to the given line. (4, 1, -2); x = 1 + t, y = 3 - 2t, z = 4 - 3t Exercise 12.4.45: x b| |a| Ja x b| |a X d =
> Find parametric equations and symmetric equations for the line. The line through the origin and the point (4, 3, -1)
> Determine whether the planes are parallel, perpendicular, or neither. If neither, find the angle between them. (Round to one decimal place.) 5x + 2y + 3z = 2, y = 4x - 6z
> Determine whether the planes are parallel, perpendicular, or neither. If neither, find the angle between them. (Round to one decimal place.) 2x - 3y = z, 4x = 3 + 6y + 2z
> (a) Estimate the area under the graph of f (x) = 1 + x2 from x = -1 to x = 2 using three rectangles and right endpoints. Then improve your estimate by using six rectangles. Sketch the curve and the approximating rectangles. (b) Repeat part (a) using left
> Determine whether the planes are parallel, perpendicular, or neither. If neither, find the angle between them. (Round to one decimal place.) x - y + 3z = 1, 3x + y - z = 2
> A curve passes through the point (0, 5) and has the property that the slope of the curve at every point P is twice the y-coordinate of P. What is the equation of the curve?
> (a) Estimate the area under the graph of f (x) = sin x from x = 0 to x = π/2 using four approximating rectangles and right endpoints. Sketch the graph and the rectangles. Is your estimate an underestimate or an overestimate? (b) Repeat part (a) using le
> (a) Estimate the area under the graph of f (x) = 1/x from x = 1 to x = 2 using four approximating rectangles and right endpoints. Sketch the graph and the rectangles. Is your estimate an underestimate or an overestimate? (b) Repeat part (a) using left en
> (a) Use six rectangles to find estimates of each type for the area under the given graph of f from x = 0 to x = 12. (i) L6 (sample points are left endpoints) (ii) R6 (sample points are right endpoints) (iii) M6 (sample points are midpoints) (b) Is L6 an
> (a) By reading values from the given graph of f, use five rectangles to find a lower estimate and an upper estimate for the area under the given graph of f from x = 0 to x = 10. In each case sketch the rectangles that you use. (b) Find new estimates usin
> Find the exact area under the cosine curve y = cos x from x = 0 to x = b, where 0 ≤ b ≤ π/2. (Use a computer algebra system both to evaluate the sum and compute the limit.) In particular, what is the area if b = π/2 ?
> Find the exact area of the region under the graph of y = e-x from 0 to 2 by using a computer algebra system to evaluate the sum and then the limit in Example 3(a). Compare your answer with the estimate obtained in Example 3(b). Example 3(a) & 3(b):
> (a) Express the area under the curve y = x5 from 0 to 2 as a limit. (b) Use a computer algebra system to find the sum in your expression from part (a). (c) Evaluate the limit in part (a).

