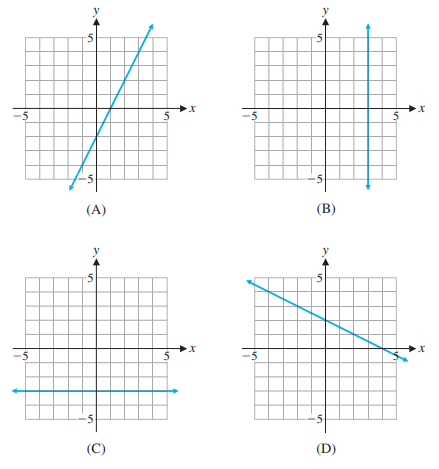
Question: Identify the graph(s) of any lines
> Find a linear regression model for the data on average annual precipitation in Table 14, where x is years since 1960 and y is precipitation (in inches). (Round regression coefficients to three decimal places). Use the model to estimate the average annual
> The percentage of male cigarette smokers in the United States declined from 25.7% in 2000 to 16.7% in 2015. (Source: Centers for Disease Control) (A) Find a linear equation relating percentage of male smokers (m) to years since 2000 (t). (B) Use this equ
> Table 13 lists fall graduate enrollment by gender in U.S. degree-granting institutions. The figure contains a scatter plot and regression line for each data set, where x represents years since 1980 and y represents enrollment (in millions). (A) Interpre
> The median household income divides the households into two groups: the half whose income is less than or equal to the median, and the half whose income is greater than the median. The median household income in the United States grew from about $30,000
> The figure contains a scatter plot of 100 data points for black walnut trees and the linear regression model for this data. (A) Interpret the slope of the model. (B) What is the effect of a 1-in. increase in Dbh? (C) Estimate the height of a black wal
> sketch a graph of each equation in a rectangular coordinate system. 8x – 3y = 24
> The airspeed indicator on some aircraft is affected by the changes in atmospheric pressure at different altitudes. A pilot can estimate the true airspeed by observing the indicated airspeed and adding to it about 1.6% for every 1,000 feet of altitude. (S
> A linear regression model for the propylene glycol data in Table 11 is P = -0.54T + 34 where P is the percentage of propylene glycol in the deicing solution and T is the temperature at which the solution freezes. (A) Draw a scatter plot of the data and
> The temperature at which water starts to boil is also linearly related to barometric pressure. Water boils at 212°F at a pressure of 29.9 inHg (inches of mercury) and at 191°F at a pressure of 28.4 inHg. (Source: biggreenegg.com) (A) Find a relationship
> A linear regression model for the operating income data in Table 10 is I = 0.82t + 15.84 where I is operating income and t is time since 2000 in years. (A) Draw a scatter plot of the data and a graph of the model on the same axes. (B) Predict Walmart&a
> A charter fishing company buys a new boat for $224,000 and assumes that it will have a trade in value of $115,200 after 16 years. (A) Find a linear model for the depreciated value V of the boat t years after it was purchased. (B) What is the depreciated
> Table 9 contains the state population and the number of licensed drivers in the state (both in millions) for the most populous states in 2014. The regression model for this data is y = 0.62x + 0.29 where x is the state population (in millions) and y is
> A clothing store sells a shirt costing $20 for $33 and a jacket costing $60 for $93. (A) If the markup policy of the store is assumed to be linear, write an equation that expresses retail price R in terms of cost C (wholesale price). (B) What does a st
> The data in Table 7 shows that the percentage of male cigarette smokers in the United States declined from 27.6% in 1997 to 16.7% in 2015. (A) Applying linear regression to the data for males in Table 7 produces the model m = -0.56t + 27.82 where m is p
> A plant can manufacture 50 tennis rackets per day for a total daily cost of $3,855 and 60 tennis rackets per day for a total daily cost of $4,245. (A) Assuming that daily cost and production are linearly related, find the total daily cost of producing x
> Table 6 lists U.S. fossil fuel consumption as a percentage of total energy consumption for selected years. A linear regression model for this data is y = -0.14x + 86.18 where x represents years since 1985 and y represents the corresponding percentage of
> write the interval as an inequality or double inequality. (-3 , 5 ]
> A small company manufactures picnic tables. The weekly fixed cost is $1,200 and the variable cost is $45 per table. Find the total weekly cost of producing x picnic tables. How many picnic tables can be produced for a total weekly cost of $4,800?
> The speed of sound through sea water is linearly related to the temperature of the water. If sound travels at 1,403 m>sec at 0°C and at 1,481 m>sec at 20°C, construct a linear model relating the speed of sound (s) and the air temperature (t). Interpret t
> Discuss the relationship among the graphs of the lines with equation y = -0.5x + b, where b is any real number.
> (A) Find the slope of the line that passes through the given points. (B) Find the standard form of the equation of the line. (C) Find the slope-intercept form of the equation of the line. ( 2, 0 ) and ( 2, -3 )
> Refer to Problem 65. If the IQ of a group of 12-year-old children varies between 80 and 140, what is the range of their mental ages? Data from Problem 65: The IQ (intelligence quotient) is found by dividing the mental age (MA), as indicated on standard
> (A) Find the slope of the line that passes through the given points. (B) Find the standard form of the equation of the line. (C) Find the slope-intercept form of the equation of the line. (1, 4) and ( 0, 4 )
> If the temperature for a 24-hour period at an Antarctic station ranged between -49°F and 14°F (that is, -49 ( F ( 14), what was the range in degrees Celsius? [Note: F = 9/5 C + 32.
> (A) Find the slope of the line that passes through the given points. (B) Find the standard form of the equation of the line. (C) Find the slope-intercept form of the equation of the line. (2, 3) and ( -3, 7 )
> The publisher in Problem 60 finds that rising prices for paper increase the variable costs to $2.70 per book. (A) Discuss possible strategies the company might use to deal with this increase in costs. (B) If the company continues to sell the books for
> (A) Find the slope of the line that passes through the given points. (B) Find the standard form of the equation of the line. (C) Find the slope-intercept form of the equation of the line. ( 1, 2 ) and ( 3, 5 )
> sketch a graph of each equation in a rectangular coordinate system.
> The publisher of a new book figures fixed costs at $92,000 and variable costs at $2.10 for each book produced. If the book is sold to distributors for $15 each, how many must be sold for the publisher to break even?
> Write the slope-intercept form of the equation of the line with the indicated slope that goes through the given point. m = 0.9; ( 2.3, 6.7 )
> A second employee of the computer store in Problem 57 is paid a base salary of $3,000 a month plus a 5% commission on all sales during the month. (A) How much must this employee sell in one month to earn a total of $4,000 for the month? (B) Determine t
> Write the slope-intercept form of the equation of the line with the indicated slope that goes through the given point.
> The local supermarket rents carpet cleaners for $20 a day. These cleaners use shampoo in a special cartridge that sells for $16 and is available only from the supermarket. A home carpet cleaner can be purchased for $300. Shampoo for the home cleaner is r
> Write the slope-intercept form of the equation of the line with the indicated slope that goes through the given point. m = -10; ( 2, -5 )
> Sale prices in a department store are obtained by marking down the retail price by 15%. That is, the sale price is obtained by subtracting 15% of the retail price from the retail price. (A) What is the sale price of a hat that has a retail price of $60?
> Write the slope-intercept form of the equation of the line with the indicated slope that goes through the given point. m = 4; ( 0, 6 )
> If the price change in houses parallels the CPI (see Table 2 in Example 10), what would a house valued at $200,000 in 2016 be valued at (to the nearest dollar) in 1960?If the price change of cars parallels the change in the CPI (see Table 2 in Example 10
> Write the equations of the vertical and horizontal lines through each point. (2.6, 3.8)
> solve for x
> Refer to Problem 49. How should you divide your money between Fund A and Fund B to produce an annual interest income of $30,000? Data From Problem 49: You have $500,000 in an IRA (Individual Retirement Account) at the time you retire. You have the optio
> Write the equations of the vertical and horizontal lines through each point. ( -5, 6)
> An all-day parking meter takes only dimes and quarters. If it contains 100 coins with a total value of $14.50, how many of each type of coin are in the meter?
> (A) Graph y = -0.8x + 5.2 in a rectangular coordinate system. (B) Find the x and y intercepts algebraically to one decimal place. (C) Graph y = -0.8x + 5.2 in a graphing calculator. (D) Find the x and y intercepts to one decimal place using trace and
> If both a and b are negative numbers and b/a is greater than 1, then is a - b positive or negative?
> Graph y = 40x + 160, x ( 0.
> solve and graph. -10 ( 8 - 3u ( -6
> Given Ax + By = 24, graph each of the following three cases in the same coordinate system. (A) A = 6 and B = 0 (B) A = 0 and B = 8 (C) A = 2 and B = 3
> solve for the indicated variable C = 5/9 (F – 32); for F
> Find the slope of the graph of each equation. -x + 8y = 4
> solve for the indicated variable. y = mx + b; for m
> Find the slope of the graph of each equation. 2x - 3y = 18
> solve for the indicated variable. y = - ⅔ x + 8 ; for x
> Find the slope of the graph of each equation. 5x - y = -2
> Solve and graph -1 ( ⅔ t + 5 ( 11
> Sketch a graph of each equation or pair of equations in a rectangular coordinate system. x = -3; y = 2
> Rewrite in equivalent logarithmic form.
> Rewrite in equivalent exponential form.
> solve and graph. -4 ≤ 5x + 6 < 21
> Rewrite in equivalent exponential form.
> Rewrite in equivalent exponential form.
> The radioactive carbon-14 (14C) in an organism at the time of its death decays according to the equation where t is time in years and A0 is the amount of 14C present at time t = 0. (See Example 3 in Section 2.5.) Estimate the age of a skull uncovered in
> Refer to Table 4. Find a logarithmic regression model (y = a + b ln x) for the total production. Estimate (to the nearest million) the production in 2024
> Use the formula in Problem 91 (with I0 = 10-16 W/cm2 ) to find the decibel ratings of the following sounds: (A) Whisper: 10-13 W/cm2 (B) Normal conversation: 3.16 * 10-10 W/cm2 (C) Heavy traffic: 10-8 W/cm2 (D) Jet plane with afterburner: 10-1 W/cm2
> Use the models constructed in Problem 89 to find the equilibrium point. Write the equilibrium price to the nearest cent and the equilibrium quantity to the nearest unit. Data from 89:
> How many years (to two decimal places) will it take an investment of $17,000 to grow to $41,000 if it is invested at 2.95% compounded continuously?
> How many years (to two decimal places) will it take $5,000 to grow to $7,500 if it is invested at 8% compounded semiannually? Compounded monthly?
> In its first 10 years the Janus Flexible Income Fund produced an average annual return of 9.58%. Assume that money invested in this fund continues to earn 9.58% compounded annually. How long (to the nearest year) will it take money invested in this fund
> Let p(x) = log x, q(x) and r(x) = x. Use a graphing calculator to draw graphs of all three functions in the same viewing window for 1 ( x ( 16. Discuss what it means for one function to be smaller than another on an interval, and then order the three fu
> Sketch a graph of each equation or pair of equations in a rectangular coordinate system. 5x - 6y = 15
> Explain why 1 is not a suitable logarithmic base.
> Graph using a calculator and point-by-point plotting. Indicate increasing and decreasing intervals. Y = 4 ln (x-3)
> Graph using a calculator and point-by-point plotting. Indicate increasing and decreasing intervals. Y = 2 ln x + 2
> Graph using a calculator and point-by-point plotting. Indicate increasing and decreasing intervals. y = ln |x|
> Graph using a calculator and point-by-point plotting. Indicate increasing and decreasing intervals. y = - ln x
> Solve each equation to four decimal places. 1.024t = 2
> Solve each equation to four decimal places ex = 0.3059
> Solve each equation to four decimal places. 10x = 153
> Find x to four decimal places. (A) log x = 2.0832 (B) log x = -1.1577 (C) ln x = 3.1336 (D) ln x = -4.3281
> Evaluate to five decimal places using a calculator. (A) log 72.604 (B) log 0.033 041 (C) ln 40,257 (D) ln 0.005 926 3
> Find the solution set.
> What are the domain and range of the function defined by y = log (x – 1) - 1?
> Explain how the graph of the equation in Problem 56 can be obtained from the graph of y = log 3 x using a simple trans formation (see Section 2.2). Data From Problem 56:
> Graph the Problems by converting to exponential form first.
> Find x
> Find x
> Find x
> discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If g is the inverse of a function , then is the inverse of g.
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. The inverse of:
> discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. The graph of a one-to-one function intersects each vertical line exactly once
> Sketch a graph of each equation or pair of equations in a rectangular coordinate system.
> solve for x 31x + 62 = 5 - 21x + 12
> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. Every polynomial function of odd degree is one-to-one.
> Find x, y, or b without using a calculator.
> Find x, y, or b without using a calculator.
> Find x, y, or b without using a calculator.
> Find x, y, or b without using a calculator.
> Find x, y, or b without using a calculator.
> Write in simpler form,
> Write in simpler form,
> Write in simpler form,