Question: If f and g are the functions
If f and g are the functions whose graphs are shown, let u (x) = f (g (x)), v (x) = g (f (x)), and w (x) = g (g (x)). Find each derivative, if it exists. If it does not exist, explain why.
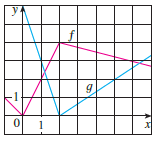
(a). u'(1)
(b). v'(1)
(c). w'(1)
Transcribed Image Text:
y f
> Find f' in terms of g'. f (x) = ln |g (x)|
> Find f' in terms of g'. f (x) = eg (x)
> Find f' in terms of g'. f (x) = g (ex)
> Find f' in terms of g'. f (x) = g (g (x))
> Find f' in terms of g'. f (x) = [g (x)]2
> Find expressions for the first five derivatives of f (x) = x2ex. Do you see a pattern in these expressions? Guess a formula for f(n)(x) and prove it using mathematical induction.
> Find f' in terms of g'. f (x) = g (x2)
> Find f' in terms of g'. f (x) = x2g (x)
> If f and g are the functions whose graphs are shown, let P (x) = f (x) g (x), Q (x) = f (x)/g (x), and C (x) = f (g (x)). Find (a) P'(2), (b) Q'(2), and (c) C'(2). 9/ f
> Suppose that h (x) f (x) g (x) and F (x) = f (g (x)), where f (2) = 3, g (2) = 5, g'(2) = 4, f'(2) = -2, and f'(5) = 11. Find (a) h'(2) and (b) F'(2).
> (a). Graph the function f (x) = x – 2 sin x in the viewing rectangle [0, 8] by [-2, 8]. (b). On which interval is the average rate of change larger: [1, 2] 0r [2, 3]. (c). At which value of is the instantaneous rate of change larger: x = 2 or x = 5? (d).
> If f (x) =xesin x, find f'(x). Graph f and f' on the same screen and comment.
> Find the limit. limu→1 u4 – 1/u3 + 5u2 – 6u
> Find the limit. limv→14+ 4 – v/|4 – v|
> Find equations of the tangent line and normal line to the curve at the given point. x2 + 4xy + y2 = 13, (2, 1)
> Sketch the graph of a function that satisfies the given conditions: f(0) = 0, f'(-2) =f'(1) = f"(9) = 0, lim f(x) = 0, lim f(x) = -, %3D %3D f'(x) < 0 on (-0, -2), (1, 6), and (9, 0), f'(x) > 0 on (-2, 1) and (6, 9), f"(x) > 0 on (-0, 0) and (12, 0)
> (a). Find equations of both lines through the point (2, -3) that are tangent to the parabola y = x2 + x. (b). Show that there is no line through the point (2, 7) that is tangent to the parabola. Then draw a diagram to see why.
> The figure shows the graph of the derivative f' of a function f. (a). Sketch the graph of f". (b). Sketch a possible graph of f. y. y = f'(x) -1 1 2 3 /4 5 6 7
> Find an equation of the tangent to the curve at the given point. x = ln t, y = t2 + 1, (0, 2)
> Find an equation of the tangent to the curve at the given point. y = x2 - 1/x2 + 1, (0, -1)
> Find an equation of the tangent to the curve at the given point. y = 4 sin2x, (π/6, 1)
> Find y" if x6 + y6 = 1.
> If f (x) = 2x, find f(n)(x).
> If g (θ) = θ sin θ, find g"(π/6).
> If f (t) = √4t + 1, find f"(2).
> Calculate y'. y = sin2 (cos √sin πx)
> Calculate y'. y = cos (e√tan 3x)
> Draw a diagram to show that there are two tangent lines to the parabola y = x2 that pass through the point (0, -4). Find the coordinates of the points where these tangent lines intersect the parabola.
> Calculate y'. y = arctan (arcsin √x)
> Calculate y'. y = sin (tan √1 + x3)
> Calculate y'. y = ln |x2 – 4/2x + 5|
> Calculate y'. y = tan2(sin θ)
> Calculate y'. y = 10 tan πθ
> Calculate y'. y = ln | sec 5x + tan 5x|
> Calculate y'. y = ecos x + cos (ex)
> Calculate y'. y = x tan-1(4x)
> Calculate y'. y = (x2 + 1)4/) (2x + 1)3(3x – 1)5
> Calculate y'. y = ln sin x – ½ sin2x
> The figure shows a lamp located three units to the right of the y-axis and a shadow created by the elliptical region x2 + 4y2 -5 3 x² + 4y? = 5
> Calculate y'. xey = y - 1
> Calculate y'. y = 3x ln x
> Calculate y'. y = √t ln (t4)
> Calculate y'. sin (xy) = x2 - y
> Calculate y'. y = (ln x) cos x
> Calculate y'. y = log5 (1 + 2x)
> Calculate y'. y = ln (x2ex)
> Calculate y'. y = ecx (c sin x – cos x)
> Calculate y'. x2 cos y + sin 2y = xy
> Calculate y'. y = sec 2θ/1 + tan 2θ
> Calculate y'. y = ln (csc 5x)
> Calculate y'. xy4 + x2y = x + 3y
> Calculate y'. y = (arcsin 2x)2
> Calculate y'. y = ((e1/x)/x2)
> Calculate y'. y = emx cos nx
> Calculate y'. y = t/1 – t2
> Calculate y'. y = e-1(t2 – 2t + 2)
> Calculate y'. y = esin2θ
> Calculate y'. y = ex/1 + x2
> Calculate y'. y = 2x√x2 + 1
> Find equations of the tangent lines to the curve y = x – 1/x + 1 that are parallel to the line x - 2y = 2.
> Calculate y'. y = 3x – 2/√2x + 1
> Calculate y'. y = √x + 1/3√x4
> Calculate y'. y = cos (tan x)
> Calculate y'. y = (x4 – 3x2 + 5)3
> Show that the length of the portion of any tangent line to the asteroid x2/3 + y2/3 = a2/3 cut off by the coordinate axes is constant.
> The cost, in dollars, of producing units of a certain commodity is C (x) = 920 + 2x – 0.02x2 + 0.00007x3 (a). Find the marginal cost function. (b). Find C"(100) and explain its meaning. (c). Compare C"(100) with the cost of producing the 101st item. (d).
> A particle moves on a vertical line so that its coordinate at time t is y = t3 – 12t + 3, t > 0. (a). Find the velocity and acceleration functions. (b). When is the particle moving upward and when is it moving downward? (c). Find the distance that the pa
> Find a parabola y = ax2 + bx + c that passes through the point (1, 4) and whose tangent lines at x = -1 and x = 5 have slopes 6 and -2, respectively.
> (a). Find an equation of the tangent to the curve y = ex that is parallel to the line x – 4y = 1. (b). Find an equation of the tangent to the curve y = ex that passes through the origin.
> The graph of a function is shown. Sketch the graph of an antiderivative F, given that F (0) = 0.
> Recall that a function f is called even if f (-x) = f (x) for all x in its domain and odd if f (-x) = -f (x) for all such x. Prove each of the following. (a). The derivative of an even function is an odd function. (b). The derivative of an odd function i
> A car starts from rest and its distance traveled is recorded in the table in 2-second intervals. (a). Estimate the speed after 6 seconds. (b). Estimate the coordinates of the inflection point of the graph of the position function. (c). What is the sign
> (a). If f (x) = 4x – tan x, -π/2 < x < π/2, find f' and f". (b). Check to see that your answers to part (a) are reasonable by comparing the graphs of f, f', and f".
> (a). If f (x) = x√5 - x, find f'(x). (b). Find equations of the tangent lines to the curve y = x√5 - x at the points (1, 2) and (4, 4). (c). Illustrate part (b) by graphing the curve and tangent lines on the same screen. (d). Check to see that your answe
> The total fertility rate at time t, denoted by F (t), is an estimate of the average number of children born to each woman (assuming that current birth rates remain constant). The graph of the total fertility rate in the United States shows the fluctuatio
> Find equations of the tangent line and normal line to the curve at the given point. y = (2 + x) e-x, (0, 2)
> Find an equation of the tangent to the curve at the given point. x = t3 – 2t2 + t + 1, y = t2 + t, (1, 0)
> The graph of the derivative f' of a function f is given. (a). On what intervals is f increasing or decreasing? (b). At what values of x does f have a local maximum or minimum? (c). Where is f concave upward or downward? (d). If f (0) = 0, sketch a poss
> The cost of living continues to rise, but at a slower rate. In terms of a function and its derivatives, what does this statement mean?
> The figure shows the graphs of f, f', and f". Identify each curve, and explain your choices. a b
> (a). Find the asymptotes of the graph of f (x) = 4 – x/3 + x and use them to sketch the graph. (b). Use your graph from part (a) to sketch the graph of f'. (c). Use the definition of a derivative to find f'(x). (d). Use a graphing device to graph f' and
> (a). Where does the normal line to the ellipse x2 – xy + y2 3 at the point (-1, 1) intersect the ellipse a second time? (b). Illustrate part (a) by graphing the ellipse and the normal line.
> The total cost of repaying a student loan at an interest rate of r % per year is C = f (r). (a). What is the meaning of the derivative f'(r)? What are its units? (b). What does the statement f'(10) = 1200 mean? (c). Is f'(r) always positive or does it ch
> According to Boyle’s Law, if the temperature of a confined gas is held fixed, then the product of the pressure P and the volume V is a constant. Suppose that, for a certain gas, PV = 800, where P is measured in pounds per square inch and V is measured in
> Use the Intermediate Value Theorem to show that there is a root of the equation in the given interval. e-x2 = x, (0, 1)
> Use the Intermediate Value Theorem to show that there is a root of the equation in the given interval. 2x3 + x2 + 2 = 0, (-2, -1)
> Show that each function is continuous on its domain. State the domain. Vx² – 9 (a) g(x) = (b) h(x) = xesin x x? – 2
> Let (a). Evaluate each limit, if it exists. (b). Where is f discontinuous? (c). Sketch the graph of f. if x<0 f(x) — { 3 — х if 0 <x<3 (x) х — 3)? if x >3 (i) lim f(x) (ii) lim f(x) (iii) lim f(x) (iv) lim f(x) (v) lim f(x) (vi) lim f(x)
> Use graphs to discover the asymptotes of the curve. Then prove what you have discovered. y = /x? + x + I – Vr? – x - x
> The graph of f is given. (a). Find each limit, or explain why it does not exist. (b). State the equations of the horizontal asymptotes. (c). State the equations of the vertical asymptotes. (d). At what numbers f is discontinuous? Explain. (i) lim
> Suppose f is a function with the property that |f (x)
> A lattice point in the plane is a point with integer coordinates. Suppose that circles with radius r are drawn using all lattice points as centers. Find the smallest value of r such that any line with slope 2/3 intersects some of these circles.
> The equation x2 – xy + y2 = 3 represents a “rotated ellipse,” that is, an ellipse whose axes are not parallel to the coordinate axes. Find the points at which this ellipse crosses the -axis and show that the tangent lines at these points are parallel.
> Suppose that three points on the parabola y = x2 have the property that their normal lines intersect at a common point. Show that the sum of their x-coordinates is 0.
> Find the two points on the curve y = x4 – 2x2 – x that have a common tangent line.
> Given an ellipse x2/a2 + y2/b2 = 1, where a ≠ b, find the equation of the set of all points from which there are two tangents to the curve whose slopes are (a) reciprocals and (b) negative reciprocals.
> Suppose that we replace the parabolic mirror of Problem 18 by a spherical mirror. Although the mirror has no focus, we can show the existence of an approximate focus. In the figure, C is a semicircle with center O. A ray of light coming in toward the mir
> A car is traveling at night along a highway shaped like a parabola with its vertex at the origin. The car starts at a point 100 m west and 100 m north of the origin and travels in an easterly direction. There is a statue located 100 m east and 50 m north
> (a). Use the identity for tan (x – y) (see Equation 14b in Appendix C) to show that if two lines L1 and L2 intersect at an angle a, then tan a = m2 – m1/1 + m1m2 where m1 and m2 are the slopes of L1 and L2, respectivel
> (a). The cubic function f (x) = x (x – 2) (x – 6) has three distinct zeros: 0, 2, and 6. Graph f and its tangent lines at the average of each pair of zeros. What do you notice? (b). Suppose the cubic function f (x) = x (x – a) (x – b) (x – c) has three d

