Question: If three different subjects are randomly selected

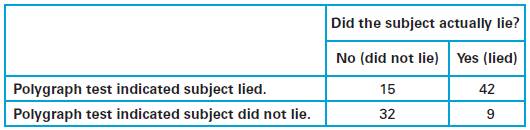
> If one of the subjects is randomly selected, find the probability of selecting someone who did not lie and had a polygraph indication of not lying.

> If one of the subjects is randomly selected, find the probability of selecting someone who lied.

> A study sponsored by AT&T and the Automobile Association of America included the sample data in the following table. a. Compare the percentage of cell phone users who had a crash to the percentage of people who did not use a cell phone and had a cras

> If P(A) = 0.65, what is the value of P(not A)?

> Using the samples of service times from all three restaurants, we obtain the analysis of variance results shown in Figure 10.7. Use a 0.05 significance level to test the claim that the three restaurants have the same mean service time.

> Using only the service times from McDonald’s, use a 0.05 significance level to test the claim that the sample is from a population with a mean of 180 seconds.

> Using only the service times from McDonald’s, construct a 95% confidence interval estimate of the population mean.

> A researcher collects paired sample data values and computes the value of the linear correlation coefficient to be 0. Based on that value, he concludes that there is no relationship between the two variables. What is wrong with this conclusion?

> In a study involving randomly selected subjects, it is found that there is a strong correlation between household income and number of visits to dentists. Is it valid to conclude that higher incomes cause people to visit dentists more often? Is it valid

> For 10 pairs of sample data values, the correlation coefficient is computed to be r = -1. What do you know about the scatterplot?

> Using the equation for the best-fit line, we find that when a slice of pizza costs $1000, the predicted subway fare is $1011. Is that predicted subway fare likely to be an accurate prediction? Why or why not?

> Does it appear that the best-fit line can be used to make a reasonably good prediction of subway fare given the cost of a slice of pizza?

> Find or estimate the value of r2. What does that value tell us?

> Can we conclude that the cost of a slice of pizza has a direct causal effect on the subway fare? Explain briefly.

> In a clinical trial of the effectiveness of a gender selection method, it is found that there is a 0.005 probability that the results could have occurred by chance. Does the method appear to be effective?

> Estimate the value of the correlation coefficient. What does that value suggest?

> Estimate the value of the linear correlation coefficient r for the points shown in the scatterplot in Figure 7.23.

> Construct a scatterplot. What does the result suggest?

> For a recent year, the fatality rate from motor vehicle crashes was reported as 10.3 per 100,000 populations. a. What is the probability that a randomly selected person will die this year as a result of a motor vehicle crash? b. If two people are randoml

> What is the meaning of small and large values of the test statistic F in ANOVA, and how do we use the value of F to decide whether to reject the null hypothesis at the 0.05 significance level?

> Describe and distinguish between the variance between samples and the variance within samples in ANOVA. How is the test statistic F related to the variance between samples and the variance within samples?

> Why is the method discussed in this section referred to as one-way analysis of variance? That is, what is “one-way” about the method?

> What does ANOVA stand for? What is the objective in using ANOVA? What form does the null hypothesis take?

> Listed below are measured amounts of greenhouse gas emissions from cars in three different categories. The measurements are in tons per year, expressed as CO2 equivalents. Use a 0.05 significance level to test the claim that the different car categories

> A student of one of the authors of this text lives in a home with a solar electric system. At the same time each day, she collected voltage readings (in volts) from a meter connected to the system and the results are listed in the accompanying table. Use

> The chest deceleration data (in g’s) from the tests described in Exercise 15 are given below. Use a 0.05 significance level to test the null hypothesis that the different size categories of cars have the same mean. Do the data suggest t

> In car crash experiments conducted by the National Transportation Safety Administration, new cars were purchased and crashed into a fixed barrier at 35 miles per hour. The subcompact cars were the Ford Escort, Honda Civic, Hyundai Accent, Nissan Sentra,

> The Binary Computer Company manufactures computer chips used in DVD players. The chips coming off the production line show a 27% yield, meaning that 27% of them are good and the others are defective. a. If one chip is randomly selected, find the probabil

> A random sample of adult females is partitioned into the age categories 18–24, 25–50, and over 50. The pulse rates of the subjects in the three different age categories are measured, and the analysis of variance result

> A random sample of M&Ms is partitioned into six categories according to color. The weights (in grams) are obtained, and the analysis of variance results are as shown in the display in Figure 10.5. a. What is the null hypothesis? b. What is the altern

> The Vertical Semirestrained Test was used to conduct flammability tests on children’s sleepwear. Pieces of fabric were burned under controlled conditions. After the burning stopped, the length of the charred portion was measured and rec

> Samples of Flesch-Kincaid Grade Level readability scores are obtained for randomly selected pages from books by Tom Clancy, J. K. Rowling, and Leo Tolstoy. The analysis of variance results from STATDISK are as shown in Figure 10.3. Assume that we want to

> A researcher obtains random samples of SAT scores from students at three different colleges. She plans to use the three sets of sample data with the method of analysis of variance. Identify the null and alternative hypotheses.

> Samples of airline departure times are obtained and compared to the scheduled departure times. Five major airlines are compared and their mean delay times are recorded. Identify the null and alternative hypotheses for applying an analysis of variance.

> An economist wants to compare the mean annual income of government employees in four different states. Analysis of variance cannot be used because there are more than three populations.

> The Atkins, Zone, Weight Watchers, and Ornish diets were tested in clinical trials. For each participant in the trials, the amount of weight loss was recorded, and results from analysis of variance show that the four diets are all effective in causing we

> In an ANOVA test for equality of mean IQ scores of students majoring in history, psychology, and art, the P-value of 0.242 is obtained. Based on the P-value, we cannot support the alternative hypothesis that at least one of the three means is different f

> In an ANOVA test for equality of mean skull breadths of Egyptian males from three different epochs, the P-value of 0.0031 is obtained. We conclude that the mean skull breadths from the three different epochs are all equal.

> Use subjective probability to estimate the probability of randomly selecting a car and selecting one that is black.

> Briefly explain the meaning of the  2 statistic. What does it tell us if the value of this statistic is small? How do you use the  2 statistic to decide whether to reject the null hypothesis?

> Explain what we mean by the observed frequency and expected frequency for each cell in a two-way table. What notation is used for the expected and observed frequencies? How do we calculate expected frequencies?

> What is a two-way table? What are the entries in its cells?

> The table below summarizes results from a survey of males aged 15 or older living in the Minhang District of China (based on data from “Cigarette Smoking in China” by Gong, Koplan, Feng, et al., Journal of the American

> The table below lists survey results obtained from a random sample of crime victims (based on data from the U.S. Department of Justice). Use a 0.01 significance level to test the claim that the type of crime is independent of whether the criminal was a s

> A random sample of 760 subjects was obtained, and each was tested for left-handed writing. Among the 240 males, 23 wrote with their left hand. Among the 520 females, 65 wrote with their left hand. The data are from the Education Resources Information Cen

> Of the 98 participants in a drug trial who were given a new experimental treatment for arthritis, 56 showed improvement. Of the 92 participants given a placebo, 49 showed improvement. Construct a two-way table for these data, and then use a 0.05 signific

> In a USA Today article about an experimental vaccine for children, the following statement appeared: “In a trial involving 1602 children, only 14 (1%) of the 1070 who received the vaccine developed the flu, compared with 95 (18%) of the

> Workers and senior-level bosses were asked if it was seriously unethical to monitor employee e-mails; the results are summarized in the following table (based on data from a Gallup poll). Use a 0.05 significance level to test the claim that the response

> In a study of high school students at least 16 years of age, researchers obtained the survey results summarized in the accompanying table (based on data from “Texting While Driving and Other Risky Motor Vehicle Behaviors Among U.S. High

> The table below includes results from polygraph (lie detector) experiments conducted by researchers Charles R. Honts (Boise State University) and Gordon H. Barland (Department of Defense Polygraph Institute). In each case, it was known if the subject lie

> Test statistic:  2= 3.849; significance level: 0.01

> Test statistic:  2= 12.336; significance level: 0.01

> Test statistic:  2= 3.957; significance level: 0.05

> Test statistic:  2 = 3.499; significance level: 0.05

> Consider the following (hypothetical) data describing a survey in which dog and cat owners are asked whether they go for daily walks. Assume that we want to use a 0.01 significance level to test the claim that whether you own a dog or a cat is independen

> Consider the following data from a study of high school students at least 16 years of age (based on data from an article in Pediatrics). Assume that we want to use a 0.05 significance level to test the claim of independence between texting while driving

> The  2 statistic from my study was close to zero, so I rejected the null hypothesis.

> In a two-way table, all of the observed frequencies are lower than the expected frequencies, so the  2 statistic is negative.

> In a two-way table, all of the observed frequencies are very close to the expected frequencies, so the  2 statistics is very small.

> If two different subjects are randomly selected without replacement, find the probability that they both lied.

> In a two-way table for major and gender, the observed frequencies were very different from the expected frequencies, so I concluded that major and gender is independent variables.

> Briefly summarize the procedure for conducting a hypothesis test for a population mean when using the t distribution. What is the difference between the procedures using the normal and t distributions?

> Briefly summarize the procedure for constructing a 95% confidence interval around a sample mean when using the t distribution. What is the difference between the procedures using the normal and t distributions?

> How do you determine the number of degrees of freedom when using a t distribution? Once you know this number, how do you find the critical value of t that you will need for building a confidence interval or conducting a statistical test?

> What is the t distribution? What factors determine its shape? Describe conditions under which you could use a t distribution instead of a normal distribution when making inferences about a population mean.

> Use the sample data listed in Exercise 18 with a 0.05 significance level to test the claim that the sample is from a population with a mean less than 1.6 W/kg.

> Use the sample data listed in Exercise 17 with a 0.05 significance level to test the claim that the sample is from a population with a mean equal to 1000 cm3.

> The Carolina Tobacco Company advertised that its best-selling non filtered cigarettes contain 40 milligrams of nicotine or less, but Consumer Advocate magazine ran tests on 10 randomly selected cigarettes and found the amounts (in milligrams) shown below

> The National Highway Traffic Safety Administration conducted crash tests of child booster seats for cars. Listed below are results from those tests, with the measurements given in the standard unit “head injury condition” (hic). The safety requirement fo

> One of the authors of this text claimed that his pulse rate was lower than the mean pulse rate of statistics students. The author’s pulse rate was measured and found to be 60 beats per minute, and the 20 students in his class measured their pulse rates.

> If one of the subjects is randomly selected, find the probability of selecting someone who lied or did not lie.

> When birth weights were recorded for a simple random sample of 16 male babies born to mothers taking a special vitamin supplement, the sample had a mean of 3.675 kilograms and a standard deviation of 0.657 kilogram (based on data from the New York State

> The mean time between failures for a Telektronic Company radio used in light aircraft is 420 hours. After 15 new radios were modified in an attempt to improve reliability, tests were conducted to measure the times between failures. The 15 radios had a me

> The U.S. Mint has a specification requiring that pennies have a mean weight of 2.5 grams (g). Thirty randomly selected pennies have a mean weight of 2.49910 g and a standard deviation of 0.01648 g. The mean weight of all pennies is assumed to be normally

> Students randomly selected 30 people and measured the accuracy of their wristwatches, with positive errors representing watches that were ahead of the correct time and negative errors representing watches that were behind the correct time. The 30 values

> A simple random sample of 16 different cereals is obtained, and the sugar content (in grams of sugar per gram of cereal) is measured for each cereal selected. Those amounts have a mean of 0.295 gram and a standard deviation of 0.168 gram. The amount of s

> Listed below are the measured “specific absorption rates” (SARs) of radiation (in watts per kilogram, or W/kg) from a sample of cell phones (when held to the head). The data are from the Environmental Working Group. The media often present reports about

> Listed below are brain volumes (in cubic centimeters, or cm3) of adult subjects used in a study. Use the sample data to construct a 95% confidence interval estimate of the mean of the normally distributed brain volumes of the entire adult population. Giv

> Listed below are lengths (in minutes) of randomly selected movies. The lengths of all movies are assumed to be normally distributed. 110 96 125 94 132 120 136 154 149 94 119 132 a. Construct a 95% confidence interval estimate of the mean length of all mo

> Each car in a sample of seven cars was tested for nitrogen-oxide emissions (in grams per mile), and the following results were obtained: 0.06, 0.11, 0.16, 0.15, 0.14, 0.08, 0.15 (based on data from the Environmental Protection Agency). Assume that nitrog

> One of the authors of this text compiled a list of actual high temperatures and a corresponding list of three-day-forecast high temperatures. The difference for each day was then found by subtracting the three-day-forecast high temperature from the actua

> A two-way table, constructed from survey results, consists of two rows representing gender (male/female) and two columns representing the response to a question (yes/no). What is the null hypothesis for a test to determine whether there is some relations

> Estimate the probability that a randomly selected prime-time television show will be interrupted with a news bulletin.

> A study was conducted to estimate hospital costs for accident victims who wore seat belts. Twenty randomly selected cases have a distribution that appears to be approximately bell-shaped with a mean of $9004 and a standard deviation of $5629 (based on da

> A simple random sample of epicenter depths of 51 earthquakes has a mean of 9.808 kilometers (km) and a standard deviation of 5.013 km. Determine the critical value of t and the margin of error, and then construct the 95% confidence interval estimate of t

> A simple random sample of men is obtained, and the elbow-to-fingertip length of each man is measured. The population of those lengths has a distribution that is normal. The sample statistics are n = 35, /= 14.5 inches, and s = 0.7 inch. Determine the cri

> A simple random sample of heights of basketball players in the NBA is obtained, and the population has a distribution that is approximately normal. The sample statistics are n = 16, /= 77.9 inches, and s = 3.50 inches. Determine the critical value of t a

> A simple random sample of IQ scores is selected from a normally distributed population of statistics professors. The sample statistics are n = 16, /= 130, and s = 10. Determine the critical value of t and the margin of error, and then construct the 95% c

> I was able to estimate the mean white blood cell count for the population of about 325 million people in the United States using a randomly selected sample of only 25 people.

> You want to test the claim that the mean annual income of all movie stars is greater than $1 million, but you know that income data are not normally distributed (they are right-skewed). Therefore you cannot use the t distribution to test the claim with a

> In testing a claim about a population mean, the t distribution is always used when the population standard deviation / is not known.

> You should always use the t distribution when the sample size is only n = 5.

> If a collection of paired sample data values yields a correlation coefficient of r = 1, then we can be very confident that causality is involved.

> If the hypothesis test of the claim described in Exercise 7 results in a P-value of 0.757, what do you conclude about the null hypothesis?

> Researchers conducted animal experiments to study smoking and lung cancer because it would have been unethical to conduct these experiments on humans.

> Describe three levels of confidence in causality that are used in the legal system, and briefly explain how these can be useful when we consider establishing causality with statistics.

> Briefly state in your own words the six guidelines that can be used in establishing causality.

> Briefly describe the correlations that made researchers suspect a link between smoking and lung cancer, and how causality was ultimately established.

> What is the difference between finding a correlation between two variables and establishing causality between two variables?

> The article “Does Vasectomy Cause Prostate Cancer?” (Chance, Vol. 10, No. 1) reports on several large studies that found an increased risk of prostate cancer among men with vasectomies. In the absence of a direct cause, several researchers attribute the