Question: In a charming 19th-century hotel, an
In a charming 19th-century hotel, an old-style elevator is connected to a counterweight by a cable that passes over a rotating disk 2.50 m in diameter (Fig. E9.18). The elevator is raised and lowered by turning the disk, and the cable does not slip on the rim of the disk but turns with it. (a) At how many rpm must the disk turn to raise the elevator at 25.0 cm/s?
(b) To start the elevator moving, it must be accelerated at 1/8 g. What must be the angular acceleration of the disk, in rad/s2?
(c) Through what angle (in radians and degrees) has the disk turned when it has raised the elevator 3.25 m between floors?
Fig. E9.18:
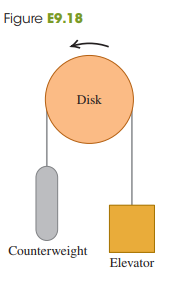
Transcribed Image Text:
Figure E9.18 Disk Counterweight Elevator
> A spring stores potential energy U0 when it is compressed a distance x0 from its uncompressed length. (a) In terms of U0, how much energy does the spring store when it is compressed (i) twice as much and (ii) half as much? (b) In terms of x0, how much mu
> A wheel is rotating about an axis that is in the z-direction. The angular velocity
> The angle u through which a disk drive turns is given by
> At t = 0 the current to a dc electric motor is reversed, resulting in an angular displacement of the motor shaft given by
> A slender rod with length L has a mass per unit length that varies with distance from the left end, where x = 0, according to dm/dx = gx, where g has units of kg/m2. (a) Calculate the total mass of the rod in terms of g and L. (b) Use Eq. (9.20) to calcu
> Use Eq. (9.20) to calculate the moment of inertia of a slender, uniform rod with mass M and length L about an axis at one end, perpendicular to the rod.
> Use Eq. (9.20) to calculate the moment of inertia of a uniform, solid disk with mass M and radius R for an axis perpendicular to the plane of the disk and passing through its center.
> A thin uniform rod of mass M and length L is bent at its center so that the two segments are now perpendicular to each other. Find its moment of inertia about an axis perpendicular to its plane and passing through (a) the point where the two segments mee
> A thin, rectangular sheet of metal has mass M and sides of length a and b. Use the parallel-axis theorem to calculate the moment of inertia of the sheet for an axis that is perpendicular to the plane of the sheet and that passes through one corner of the
> (a) For the thin rectangular plate shown in part (d) of Table 9.2, find the moment of inertia about an axis that lies in the plane of the plate, passes through the center of the plate, and is parallel to the axis shown. (b) Find the moment of inertia of
> A child is pushing a merry-go-round. The angle through which the merry-go-round has turned varies with time according to
> Tendons are strong elastic fibers that attach muscles to bones. To a reasonable approximation, they obey Hooke’s law. In laboratory tests on a particular tendon, it was found that, when a 250-g object was hung from it, the tendon stretched 1.23 cm. (a)
> About what axis will a uniform, balsa-wood sphere have the same moment of inertia as does a thin-walled, hollow, lead sphere of the same mass and radius, with the axis along a diameter?
> Find the moment of inertia of a hoop (a thin-walled, hollow ring) with mass M and radius R about an axis perpendicular to the hoop’s plane at an edge.
> If we multiply all the design dimensions of an object by a scaling factor f, its volume and mass will be multiplied by f3. (a) By what factor will its moment of inertia be multiplied? (b) If a 1/48-scale model has a rotational kinetic energy of 2.5 J, wh
> A uniform 2.00-m ladder of mass 9.00 kg is leaning against a vertical wall while making an angle of 53.0° with the floor. A worker pushes the ladder up against the wall until it is vertical. What is the increase in the gravitational potential energy of t
> A thin, light wire is wrapped around the rim of a wheel (Fig. E9.45). The wheel rotates without friction about a stationary horizontal axis that passes through the center of the wheel. The wheel is a uniform disk with radius R = 0.280 m. An object of mas
> A bucket of mass m is tied to a massless cable that is wrapped around the outer rim of a frictionless uniform pulley of radius R, similar to the system shown in Fig. E9.43. In terms of the stated variables, what must be the moment of inertia of the pulle
> A frictionless pulley has the shape of a uniform solid disk of mass 2.50 kg and radius 20.0 cm. A 1.50-kg stone is attached to a very light wire that is wrapped around the rim of the pulley (Fig. E9.43), and the system is released from rest. (a) How far
> A light, flexible rope is wrapped several times around a hollow cylinder, with a weight of 40.0 N and a radius of 0.25 m, that rotates without friction about a fixed horizontal axis. The cylinder is attached to the axle by spokes of a negligible moment o
> Energy is to be stored in a 70.0-kg flywheel in the shape of a uniform solid disk with radius R = 1.20 m. To prevent structural failure of the flywheel, the maximum allowed radial acceleration of a point on its rim is 3500 m/s2. What is the maximum kinet
> You need to design an industrial turntable that is 60.0 cm in diameter and has a kinetic energy of 0.250 J when turning at 45.0 rpm (rev/min). (a) What must be the moment of inertia of the turntable about the rotation axis? (b) If your workshop makes thi
> A force of 520 N keeps a certain spring stretched a distance of 0.200 m. (a) What is the potential energy of the spring when it is stretched 0.200 m? (b) What is its potential energy when it is compressed 5.00 cm?
> A fan blade rotates with angular velocity given by
> The flywheel of a gasoline engine is required to give up 500 J of kinetic energy while its angular velocity decreases from 650 rev/min to 520 rev/min. What moment of inertia is required?
> A hollow spherical shell has mass 8.20 kg and radius 0.220 m. It is initially at rest and then rotates about a stationary axis that lies along a diameter with a constant acceleration of 0.890 rad/s2. What is the kinetic energy of the shell after it has t
> A uniform sphere with mass 28.0 kg and radius 0.380 m is rotating at constant angular velocity about a stationary axis that lies along a diameter of the sphere. If the kinetic energy of the sphere is 236 J, what is the tangential velocity of a point on t
> A wheel is turning about an axis through its center with constant angular acceleration. Starting from rest, at t = 0, the wheel turns through 8.20 revolutions in 12.0 s. At t = 12.0 s the kinetic energy of the wheel is 36.0 J. For an axis through its cen
> A compound disk of outside diameter 140.0 cm is made up of a uniform solid disk of radius 50.0 cm and area density 3.00 g/cm2 surrounded by a concentric ring of inner radius 50.0 cm, outer radius 70.0 cm, and area density 2.00 g/cm2. Find the moment of i
> An airplane propeller is 2.08 m in length (from tip to tip) with mass 117 kg and is rotating at 2400 rpm (rev/min) about an axis through its center. You can model the propeller as a slender rod. (a) What is its rotational kinetic energy? (b) Suppose that
> A wagon wheel is constructed as shown in Fig. E9.33. The radius of the wheel is 0.300 m, and the rim has mass 1.40 kg. Each of the eight spokes that lie along a diameter and are 0.300 m long has mass 0.280 kg. What is the moment of inertia of the wheel a
> You are a project manager for a manufacturing company. One of the machine parts on the assembly line is a thin, uniform rod that is 60.0 cm long and has mass 0.400 kg. (a) What is the moment of inertia of this rod for an axis at its center, perpendicular
> A uniform bar has two small balls glued to its ends. The bar is 2.00 m long and has mass 4.00 kg, while the balls each have mass 0.300 kg and can be treated as point masses. Find the moment of inertia of this combination about an axis (a) perpendicular t
> An ideal spring of negligible mass is 12.00 cm long when nothing is attached to it. When you hang a 3.15-kg weight from it, you measure its length to be 13.40 cm. If you wanted to store 10.0 J of potential energy in this spring, what would be its total l
> Small blocks, each with mass m, are clamped at the ends and at the center of a rod of length L and negligible mass. Compute the moment of inertia of the system about an axis perpendicular to the rod and passing through (a) the center of the rod and (b) a
> The angular velocity of a flywheel obeys the equation
> Calculate the moment of inertia of each of the following uniform objects about the axes indicated. Consult Table 9.2 as needed. (a) A thin 2.50-kg rod of length 75.0 cm, about an axis perpendicular to it and passing through (i) one end and (ii) its cente
> Four small spheres, each of which you can regard as a point of mass 0.200 kg, are arranged in a square 0.400 m on a side and connected by extremely light rods (Fig. E9.28). Find the moment of inertia of the system about an axis (a) through the center of
> According to the shop manual, when drilling a 12.7-mm-diameter hole in wood, plastic, or aluminum, a drill should have a speed of 1250 rev/min. For a 12.7-mm- diameter drill bit turning at a constant 1250 rev/min, find (a) the maximum linear speed of any
> At t = 3.00 s a point on the rim of a 0.200-m-radius wheel has a tangential speed of 50.0 m/s as the wheel slows down with a tangential acceleration of constant magnitude 10.0 m/s2. (a) Calculate the wheel’s constant angular acceleration. (b) Calculate t
> An advertisement claims that a centrifuge takes up only 0.127 m of bench space but can produce a radial acceleration of 3000g at 5000 rev/min. Calculate the required radius of the centrifuge. Is the claim realistic?
> An electric turntable 0.750 m in diameter is rotating about a fixed axis with an initial angular velocity of 0.250 rev>s and a constant angular acceleration of 0.900 rev/s2. (a) Compute the angular velocity of the turntable after 0.200 s. (b) Through how
> A flywheel with a radius of 0.300 m starts from rest and accelerates with a constant angular acceleration of 0.600 rad/s2. Compute the magnitude of the tangential acceleration, the radial acceleration, and the resultant acceleration of a point on its rim
> You are to design a rotating cylindrical axle to lift 800-N buckets of cement from the ground to a rooftop 78.0 m above the ground. The buckets will be attached to a hook on the free end of a cable that wraps around the rim of the axle; as the axle turns
> A 10.0-kg microwave oven is pushed 6.00 m up the sloping surface of a loading ramp inclined at an angle of 36.9° above the horizontal, by a constant force
> A wheel of diameter 40.0 cm starts from rest and rotates with a constant angular acceleration of 3.00 rad/s2. Compute the radial acceleration of a point on the rim for the instant the wheel completes its second revolution from the relationship (a) arad =
> A compact disc (CD) stores music in a coded pattern of tiny pits 10-7 m deep. The pits are arranged in a track that spirals outward toward the rim of the disc; the inner and outer radii of this spiral are 25.0 mm and 58.0 mm, respectively. As the disc sp
> An airplane propeller is rotating at 1900 rpm (rev/min). (a) Compute the propeller’s angular velocity in rad/s. (b) How many seconds does it take for the propeller to turn through 35°?
> Using Appendix F, along with the fact that the earth spins on its axis once per day, calculate (a) the earth’s orbital angular speed (in rad/s) due to its motion around the sun, (b) its angular speed (in rad/s) due to its axial spin, (c) the tangential s
> A safety device brings the blade of a power mower from an initial angular speed of
> At t = 0 a grinding wheel has an angular velocity of 24.0 rad/s. It has a constant angular acceleration of 30.0 rad/s2 until a circuit breaker trips at t = 2.00 s. From then on, it turns through 432 rad as it coasts to a stop at constant angular accelera
> A high-speed flywheel in a motor is spinning at 500 rpm when a power failure suddenly occurs. The flywheel has mass 40.0 kg and diameter 75.0 cm. The power is off for 30.0 s, and during this time the flywheel slows due to friction in its axle bearings. D
> A circular saw blade 0.200 m in diameter starts from rest. In 6.00 s it accelerates with constant angular acceleration to an angular velocity of 140 rad/s. Find the angular acceleration and the angle through which the blade has turned.
> A turntable rotates with a constant 2.25 rad/s2 angular acceleration. After 4.00 s it has rotated through an angle of 30.0 rad. What was the angular velocity of the wheel at the beginning of the 4.00-s interval?
> Tarzan, in one tree, sights Jane in another tree. He grabs the end of a vine with length 20 m that makes an angle of 45° with the vertical, steps off his tree limb, and swings down and then up to Jane’s open arms. When he arrives, his vine makes an angle
> A 90.0kg mail bag hangs by a vertical rope 3.5 m long. A postal worker then displaces the bag to a position 2.0 m sideways from its original position, always keeping the rope taut. (a) What horizontal force is necessary to hold the bag in the new positi
> When a gas expands adiabatically, it does work on its surroundings. But if there is no heat input to the gas, where does the energy come from to do the work?
> When a gas surrounded by air is compressed adiabatically, its temperature rises even though there is no heat input to the gas. Where does the energy come from to raise the temperature?
> In a constant-volume process, dU = nCV dT. But in a constant-pressure process, it is not true that dU = nCp dT. Why not?
> Applying the same considerations as in Question Q19.17, explain why the island of Niihau, a few kilometers to the southwest of Kauai, is almost a desert and farms there need to be irrigated. Question Q19.17: The prevailing winds on the Hawaiian island
> The prevailing winds on the Hawaiian island of Kauai blow from the northeast. The winds cool as they go up the slope of Mt. Waialeale (elevation 1523 m), causing water vapor to condense and rain to fall. There is much more precipitation at the summit tha
> What would be the efficiency of a Carnot engine operating with TH = TC ? What would be the efficiency if TC = 0 K and TH were any temperature above 0 K? Interpret your answers.
> In the carburetor of an aircraft or automobile engine, air flows through a relatively small aperture and then expands. In cool, foggy weather, ice sometimes forms in this aperture even though the outside air temperature is above freezing. Why?
> When you use a hand pump to inflate the tires of your bicycle, the pump gets warm after a while. Why? What happens to the temperature of the air in the pump as you compress it? Why does this happen? When you raise the pump handle to draw outside air into
> Real heat engines, like the gasoline engine in a car, always have some friction between their moving parts, although lubricants keep the friction to a minimum. Would a heat engine with completely frictionless parts be 100% efficient? Why or why not? Does
> An ideal gas expands while the pressure is kept constant. During this process, does heat flow into the gas or out of the gas? Justify your answer.
> Household refrigerators have arrays or coils of tubing on the outside, usually at the back or bottom. When the refrigerator is running, the tubing becomes quite hot. Where does the heat come from?
> The efficiency of heat engines is high when the temperature difference between the hot and cold reservoirs is large. Refrigerators, on the other hand, work better when the temperature difference is small. Thinking of the mechanical refrigeration cycle sh
> In an adiabatic process for an ideal gas, the pressure decreases. In this process does the internal energy of the gas increase or decrease? Explain.
> Imagine a gas made up entirely of negatively charged electrons. Like charges repel, so the electrons exert repulsive forces on each other. Would you expect that the temperature of such a gas would rise, fall, or stay the same in a free expansion? Why?
> An electric motor has its shaft coupled to that of an electric generator. The motor drives the generator, and some current from the generator is used to run the motor. The excess current is used to light a home. What is wrong with this scheme?
> Imagine a special air filter placed in a window of a house. The tiny holes in the filter allow only air molecules moving faster than a certain speed to exit the house, and allow only air molecules moving slower than that speed to enter the house from out
> When ice melts at 00C, its volume decreases. Is the internal energy change greater than, less than, or equal to the heat added? How can you tell?
> If you are told the initial and final states of a system and the associated change in internal energy, can you determine whether the internal energy change was due to work or to heat transfer? Explain.
> A pot is half-filled with water, and a lid is placed on it, forming a tight seal so that no water vapor can escape. The pot is heated on a stove, forming water vapor inside the pot. The heat is then turned off and the water vapor condenses back to liquid
> It is not correct to say that a body contains a certain amount of heat, yet a body can transfer heat to another body. How can a body give away something it does not have in the first place?
> For the following processes, is the work done by the system (defined as the expanding or contracting gas) on the environment positive or negative? (a). expansion of the burned gasoline–air mixture in the cylinder of an automobile engine; (b). opening a
> You bake chocolate chip cookies and put them, still warm, in a container with a loose (not airtight) lid. What kind of process does the air inside the container undergo as the cookies gradually cool to room temperature (isothermal, isochoric, adiabatic,
> The graph in Fig. P19.36 shows a pV-diagram for 3.25 mol of ideal helium (He) gas. Part ca of this process is isothermal. Fig. P19.36: (a). Find the pressure of the He at point a. (b). Find the temperature of the He at points a, b, and c. (c) How m
> Figure P19.35 shows the pV-diagram for a process in which the temperature of the ideal gas remains constant at 85°C. Figure P19.35: (a). How many moles of gas are involved? (b). What volume does this gas occupy at a? (c). How much work wa
> One-half mole of an ideal gas is taken from state a to state c as shown in Fig. P19.34. Fig. P19.34: (a). Calculate the final temperature of the gas. (b). Calculate the work done on (or by) the gas as it moves from state a to state c. (c). Does hea
> A quantity of air is taken from state a to state b along a path that is a straight line in the pV diagram (Fig. P19.33). Fig. P19.33: (a). In this process, does the temperature of the gas increase, decrease, or stay the same? Explain. (b). If Va = 0.
> A cylinder with a frictionless, movable piston like that shown in Fig. 19.5 contains a quantity of helium gas. Initially the gas is at 1.00 × 105 Pa and 300 K and occupies a volume of 1.50 L. The gas then undergoes two processes. In the firs
> Nitrogen gas in an expandable container is cooled from 50.0 0C to 10.0 0C with the pressure held constant at 3.00 × 105 Pa. The total heat liberated by the gas is 2.50 × 104 J. Assume that the gas may be treated as ideal. Find (a) the number of moles of
> Starting with 2.50 mol of N2 gas (assumed to be ideal) in a cylinder at 1.00 atm and 20.0 0C, a chemist first heats the gas at constant volume, adding 1.36 × 104 J of heat, then continues heating and allows the gas to expand at constant pressure to twice
> (a). One-third of a mole of He gas is taken along the path abc shown in Fig. P19.44. Assume that the gas may be treated as ideal. How much heat is transferred into or out of the gas? (b). If the gas instead went directly from state a to state c along th
> Figure P19.43 shows a pV-diagram for 0.0040 mol of ideal H2 gas. The temperature of the gas does not change during segment bc. Figure P19.43: (a). What volume does this gas occupy at point c? (b). Find the temperature of the gas at points a, b, and c
> Three moles of an ideal gas are taken around cycle acb shown in Fig. P19.42. For this gas, Cp = 29.1 J/mol ∙ K. Process ac is at constant pressure, process ba is at constant volume, and process cb is adiabatic. The temperatures of the g
> You hold an inflated balloon over a hot-air vent in your house and watch it slowly expand. You then remove it and let it cool back to room temperature. During the expansion, which was larger: the heat added to the balloon or the work done by the air insi
> Two moles of an ideal monatomic gas go through the cycle abc. For the complete cycle, 800 J of heat flows out of the gas. Process ab is at constant pressure, and process bc is at constant volume. States a and b have temperatures Ta = 200 K and Tb = 300 K
> Three moles of argon gas (assumed to be an ideal gas) originally at 1.50 × 104 Pa and a volume of 0.0280 m3 are first heated and expanded at constant pressure to a volume of 0.0435 m3, then heated at constant volume until the pressure reaches 3.50 × 104
> A volume of air (assumed to be an ideal gas) is first cooled without changing its volume and then expanded without changing its pressure, as shown by path abc in Fig. P19.39. Fig. P19.39: (a). How does the final temperature of the gas compare with it
> In a hospital, pure oxygen may be delivered at 50 psi (gauge pressure) and then mixed with N2O. What volume of oxygen at 20°C and 50 psi (gauge pressure) should be mixed with 1.7 kg of N2O to get a 50%/50% mixture by volume at 20°C? (a). 0.21 m3; (b). 0
> You have a cylinder that contains 500 L of the gas mixture pressurized to 2000 psi (gauge pressure). A regulator sets the gas flow to deliver 8.2 L/min at atmospheric pressure. Assume that this flow is slow enough that the expansion is isothermal and the
> In another test, the valve of a 500-L cylinder full of the gas mixture at 2000 psi (gauge pressure) is opened wide so that the gas rushes out of the cylinder very rapidly. Why might some N2O condense during this process? (a). This is an isochoric proces
> A thermodynamic system is taken from state a to state c in Fig. P19.38 along either path abc or path adc. Along path abc, the work W done by the system is 450 J. Along path adc, W is 120 J. The internal energies of each of the four states shown in the fi
> The power output of an automobile engine is directly proportional to the mass of air that can be forced into the volume of the engine’s cylinders to react chemically with gasoline. Many cars have a turbocharger, which compresses the air before it enters
> You place a quantity of gas into a metal cylinder that has a movable piston at one end. No gas leaks out of the cylinder as the piston moves. The external force applied to the piston can be varied to change the gas pressure as you move the piston to chan
> You compress a gas in an insulated cylinder— no heat flows into or out of the gas. The gas pressure is fairly low, so treating the gas as ideal is a good approximation. When you measure the pressure as a function of the volume of the ga
> Is it a violation of the second law of thermodynamics to convert mechanical energy completely into heat? To convert heat completely into work? Explain your answers.

