Question: In Fig. E26.11, R1 = 3.00
In Fig. E26.11, R1 = 3.00 Ω, R2 = 6.00 Ω, and R3 = 5.00 Ω. The battery has negligible internal resistance. The current I2 through R2 is 4.00 A.
Fig. E26.11:
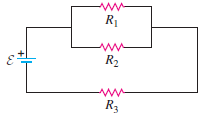
(a). What are the currents I1 and I3?
(b). What is the emf of the battery?
Transcribed Image Text:
ww R1 R2 R3
> Consider the circuit shown in Fig. E26.16. The current through the 6.00-Ω resistor is 4.00 A, in the direction shown. What are the currents through the 25.0-Ω and 20.0-Ω resistors? Fig. E26.16: 4.00 A 6.00 N ww 2
> The magnetic poles of a small cyclotron produce a magnetic field with magnitude 0.85 T. The poles have a radius of 0.40 m, which is the maximum radius of the orbits of the accelerated particles. (a). What is the maximum energy to which protons (q = 1.60
> An L-C circuit consists of a 60.0-mH inductor and a 250-µF capacitor. The initial charge on the capacitor is 6.00 µC, and the initial current in the inductor is zero. (a). What is the maximum voltage across the capacitor? (b). What is the maximum curre
> Your latest invention is a car alarm that produces sound at a particularly annoying frequency of 3500 Hz. To do this, the car-alarm circuitry must produce an alternating electric current of the same frequency. That’s why your design includes an inductor
> A very long, straight solenoid with a crosssectional area of 2.00 cm2 is wound with 90.0 turns of wire per centimeter. Starting at t = 0, the current in the solenoid is increasing according to i(t) = (0.160 A/s2) t2. A secondary winding of 5 turns encirc
> A small solid conductor with radius a is supported by insulating, nonmagnetic disks on the axis of a thin-walled tube with inner radius b. The inner and outer conductors carry equal currents i in opposite directions. (a). Use Ampere’s law to find the ma
> A coil has 400 turns and self-inductance 7.50 mH. The current in the coil varies with time according to i = (680 mA) cos (pt/0.0250 s). (a). What is the maximum emf induced in the coil? (b). What is the maximum average flux through each turn of the coi
> One solenoid is centered inside another. The outer one has a length of 50.0 cm and contains 6750 coils, while the coaxial inner solenoid is 3.0 cm long and 0.120 cm in diameter and contains 15 coils. The current in the outer solenoid is changing at 49.2
> Two long, parallel wires are separated by a distance of 2.50 cm. The force per unit length that each wire exerts on the other is 4.00 × 10-5 N/m, and the wires repel each other. The current in one wire is 0.600 A. (a). What is the current in the second
> An inductor is connected to the terminals of a battery that has an emf of 16.0 V and negligible internal resistance. The current is 4.86 mA at 0.940 ms after the connection is completed. After a long time, the current is 6.45 mA. What are (a). the resist
> An L-R-C series circuit has L = 0.450 H, C = 2.50 × 10-5 F, and resistance R. (a). What is the angular frequency of the circuit when R = 0? (b). What value must R have to give a 5.0% decrease in angular frequency compared to the value calculated in par
> An L-R-C series circuit has L = 0.600 H and C = 3.00 µF. (a). Calculate the angular frequency of oscillation for the circuit when R = 0. (b). What value of R gives critical damping? (c). What is the oscillation frequency
> In the circuit of Fig. E26.15, each resistor represents a light bulb. Let R1 = R2 = R3 = R4 = 4.50 Ω and
> An L-C circuit containing an 80.0-mH inductor and a 1.25-nF capacitor oscillates with a maximum current of 0.750 A. Calculate: (a). the maximum charge on the capacitor and (b). the oscillation frequency of the circuit. (c). Assuming the capacitor had
> In an L-C circuit, L = 85.0 mH and C = 3.20 µF. During the oscillations the maximum current in the inductor is 0.850 mA. (a). What is the maximum charge on the capacitor? (b). What is the magnitude of the charge on the capacitor at an instant when the c
> In Fig. 30.11 switch S1 is closed while switch S2 is kept open. The inductance is L = 0.380 H, the resistance is R = 48.0 Ω, and the emf of the battery is 18.0 V. At time t after S1 is closed, the current in the circuit is increasing
> A 35.0-V battery with negligible internal resistance, a 50.0 Ω resistor, and a 1.25-mH inductor with negligible resistance are all connected in series with an open switch. The switch is suddenly closed. (a). How long after closing the switch will the cu
> In a proton accelerator used in elementary particle physics experiments, the trajectories of protons are controlled by bending magnets that produce a magnetic field of 4.80 T. What is the magnetic-field energy in a 10.0-cm3 volume of space where B = 4.80
> An air-filled toroidal solenoid has 300 turns of wire, a mean radius of 12.0 cm, and a cross-sectional area of 4.00 cm2. If the current is 5.00 A, calculate: (a). the magnetic field in the solenoid; (b). the self-inductance of the solenoid; (c). the en
> Two long, parallel wires are separated by a distance of 0.400 m (Fig. E28.29). The currents I1 and I2 have the directions shown. Fig. E28.29: (a). Calculate the magnitude of the force exerted by each wire on a 1.20-m length of the other. Is the force
> An air-filled toroidal solenoid has a mean radius of 15.0 cm and a cross-sectional area of 5.00 cm2. When the current is 12.0 A, the energy stored is 0.390 J. How many turns does the winding have?
> At the instant when the current in an inductor is increasing at a rate of 0.0640 A/s, the magnitude of the self-induced emf is 0.0160 V. (a). What is the inductance of the inductor? (b). If the inductor is a solenoid with 400 turns, what is the average
> (a). A long, straight solenoid has N turns, uniform cross-sectional area A, and length l. Show that the inductance of this solenoid is given by the equation L = µ0AN2/l. Assume that the magnetic field is uniform inside the solenoid and zero outside. (You
> A long, straight solenoid has 800 turns. When the current in the solenoid is 2.90 A, the average flux through each turn of the solenoid is 3.25 × 10-3 Wb. What must be the magnitude of the rate of change of the current in order for the self-induced emf t
> Compute the equivalent resistance of the network in Fig. E26.14, and find the current in each resistor. The battery has negligible internal resistance. Fig. E26.14: ε- 48.0 V r-0 1.00 Ω 3.00 Ω ww 7.00 Ω 5.00 Ω
> If two resistors R1 and R2 (R2 > R1) are connected in series as shown in Fig. Q26.5, which of the following must be true? In each case justify your answer. Fig. Q26.5: (a). I1 = I2 = I3. (b). The current is greater in R1 than in R2. (c). The ele
> When the current in a toroidal solenoid is changing at a rate of 0.0260 A/s, the magnitude of the induced emf is 12.6 mV. When the current equals 1.40 A, the average flux through each turn of the solenoid is 0.00285 Wb. How many turns does the solenoid h
> A toroidal solenoid with mean radius r and cross-sectional area A is wound uniformly with N1 turns. A second toroidal solenoid with N2 turns is wound uniformly on top of the first, so that the two solenoids have the same cross-sectional area and mean rad
> Two toroidal solenoids are wound around the same form so that the magnetic field of one passes through the turns of the other. Solenoid 1 has 700 turns, and solenoid 2 has 400 turns. When the current in solenoid 1 is 6.52 A, the average flux through each
> Two coils have mutual inductance M = 3.25 × 10-4 H. The current i1 in the first coil increases at a uniform rate of 830 A/s. (a). What is the magnitude of the induced emf in the second coil? Is it constant? (b). Suppose that the current described is in
> The body contains many small currents caused by the motion of ions in the organs and cells. Measurements of the magnetic field around the chest due to currents in the heart give values of about 10 µG. Although the actual currents are rather complicated,
> Suppose that the parallel plates in Fig. 29.23 have an area of 3.00 cm2 and are separated by a 2.50-mm-thick sheet of dielectric that completely fills the volume between the plates. The dielectric has dielectric constant 4.70. (You can ignore fringing ef
> A long, thin solenoid has 400 turns per meter and radius 1.10 cm. The current in the solenoid is increasing at a uniform rate di/dt. The induced electric field at a point near the center of the solenoid and 3.50 cm from its axis is 8.00 × 10-6 V/m. Calcu
> Airplanes and trains move through the earth’s magnetic field at rather high speeds, so it is reasonable to wonder whether this field can have a substantial effect on them. We shall use a typical value of 0.50 G for the earth’s field. (a). The French TGV
> How fast (in m/s and mph) would a 5.00-cm copper bar have to move at right angles to a 0.650-T magnetic field to generate 1.50 V (the same as a AA battery) across its ends? Does this seem like a practical way to generate electricity?
> The current in the long, straight wire AB shown in Fig. E29.7 is upward and is increasing steadily at a rate di/dt. Figure E29.7: (a). At an instant when the current is i, what are the magnitude and direction of the field B at a distance r to the righ
> A coil 4.00 cm in radius, containing 500 turns, is placed in a uniform magnetic field that varies with time according to B = (0.0120 T/s) t + (3.00 × 10-5 T/s4) t4. The coil is connected to a 600-Ω resistor, and its plane is perpendicular to the magnetic
> In Fig. E26.11 the battery has emf 35.0 V and negligible internal resistance. R1 = 5.00 Ω. The current through R1 is 1.50 A, and the current through R3 = 4.50 A. What are the resistances R2 and R3? Fig. E26.11: ww R1 R2 R3
> A circular loop of wire with a radius of 12.0 cm and oriented in the horizontal xy-plane is located in a region of uniform magnetic field. A field of 1.5 T is directed along the positive z-direction, which is upward. (a). If the loop is removed from the
> In a physics laboratory experiment, a coil with 200 turns enclosing an area of 12 cm2 is rotated in 0.040 s from a position where its plane is perpendicular to the earth’s magnetic field to a position where its plane is parallel to the field. The earth’s
> The armature of a small generator consists of a flat, square coil with 120 turns and sides with a length of 1.60 cm. The coil rotates in a magnetic field of 0.0750 T. What is the angular speed of the coil if the maximum emf produced is 24.0 mV?
> A very long, straight horizontal wire carries a current such that 8.20 × 1018 electrons per second pass any given point going from west to east. What are the magnitude and direction of the magnetic field this wire produces at a point 4.00 cm directly abo
> In many magnetic resonance imaging (MRI) systems, the magnetic field is produced by a superconducting magnet that must be kept cooled below the superconducting transition temperature. If the cryogenic cooling system fails, the magnet coils may lose their
> A single loop of wire with an area of 0.0900 m2 is in a uniform magnetic field that has an initial value of 3.80 T, is perpendicular to the plane of the loop, and is decreasing at a constant rate of 0.190 T/s. (a). What emf is induced in this loop? (b)
> The current in the windings of a toroidal solenoid is 2.400 A. There are 500 turns, and the mean radius is 25.00 cm. The toroidal solenoid is filled with a magnetic material. The magnetic field inside the windings is found to be 1.940 T. Calculate (a). t
> A toroidal solenoid with 400 turns of wire and a mean radius of 6.0 cm carries a current of 0.25 A. The relative permeability of the core is 80. (a). What is the magnetic field in the core? (b). What part of the magnetic field is due to atomic currents?
> A wooden ring whose mean diameter is 14.0 cm is wound with a closely spaced toroidal winding of 600 turns. Compute the magnitude of the magnetic field at the center of the cross section of the windings when the current in the windings is 0.650 A.
> A magnetic field of 37.2 T has been achieved at the MIT Francis Bitter National Magnetic Laboratory. Find the current needed to achieve such a field (a). 2.00 cm from a long, straight wire; (b). at the center of a circular coil of radius 42.0 cm that h
> A 15.0-cm-long solenoid with radius 0.750 cm is closely wound with 600 turns of wire. The current in the windings is 8.00 A. Compute the magnetic field at a point near the center of the solenoid.
> A solenoid that is 35 cm long and contains 450 circular coils 2.0 cm in diameter carries a 1.75-A current. (a). What is the magnetic field at the center of the solenoid, 1.0 cm from the coils? (b). Suppose we now stretch out the coils to make a very lo
> As a new electrical technician, you are designing a large solenoid to produce a uniform 0.150-T magnetic field near the center of the solenoid. You have enough wire for 4000 circular turns. This solenoid must be 55.0 cm long and 2.80 cm in diameter. What
> Two very long insulated wires perpendicular to each other in the same plane carry currents as shown in Fig. E28.27. Find the magnitude of the net magnetic field these wires produce at points P and Q if the 10.0-A current is Fig. E28.27: (a). to the ri
> The amount of meat in prehistoric diets can be determined by measuring the ratio of the isotopes 15N to 14N in bone from human remains. Carnivores concentrate 15N, so this ratio tells archaeologists how much meat was consumed. For a mass spectrometer tha
> A closely wound coil has a radius of 6.00 cm and carries a current of 2.50 A. How many turns must it have if, at a point on the coil axis 6.00 cm from the center of the coil, the magnetic field is 6.39 × 10-4 T?
> Calculate the magnitude and direction of the magnetic field at point P due to the current in the semicircular section of wire shown in Fig. E28.34. (Hint: Does the current in the long, straight section of the wire produce any field at P?) Fig. E28.34:
> Currents in dc transmission lines can be 100 A or higher. Some people are concerned that the electromagnetic fields from such lines near their homes could pose health dangers. For a line that has current 150 A and a height of 8.0 m above the ground, what
> Lightning bolts can carry currents up to approximately 20 kA. We can model such a current as the equivalent of a very long, straight wire. (a). If you were unfortunate enough to be 5.0 m away from such a lightning bolt, how large a magnetic field would y
> A straight wire carries a 10.0-A current (Fig. E28.9). ABCD is a rectangle with point D in the middle of a 1.10-mm segment of the wire and point C in the wire. Find the magnitude and direction of the magnetic field due to this segment at Fig. E28.9:
> A square wire loop 10.0 cm on each side carries a clockwise current of 8.00 A. Find the magnitude and direction of the magnetic field at its center due to the four 1.20-mm wire segments at the midpoint of each side.
> A wire carrying a 28.0-A current bends through a right angle. Consider two 2.00-mm segments of wire, each 3.00 cm from the bend (Fig. E28.13). Find the magnitude and direction of the magnetic field these two segments produce at point P, which is midway b
> A short current element d
> The power rating of a resistor is the maximum power the resistor can safely dissipate without too great a rise in temperature and hence damage to the resistor. (a). If the power rating of a 15-k Ω resistor is 5.0 W, what is the maximum allowable potenti
> A negative charge q = -3.60 × 10-6 C is located at the origin and has velocity
> Four very long, current carrying wires in the same plane intersect to form a square 40.0 cm on each side, as shown in Fig. E28.26. Find the magnitude and direction of the current I so that the magnetic field at the center of the square is zero. Fig. E28
> A -4.80-µC charge is moving at a constant speed of 6.80 × 105 m/s in the +x-direction relative to a reference frame. At the instant when the point charge is at the origin, what is the magnetic-field vector it produces at the following points: (a). x = 0
> In the Bohr model of the hydrogen atom, the electron moves in a circular orbit of radius 5.3 × 10-11 m with a speed of 2.2 × 106 m/s. If we are viewing the atom in such a way that the electron’s orbit is in the plane of the paper with the electron moving
> Let Fig. E27.49 represent a strip of an unknown metal of the same dimensions as those of the silver ribbon in Exercise 27.49. When the magnetic field is 2.29 T and the current is 78.0 A, the Hall emf is found to be 131 mV. What does the simplified model
> Singly ionized (one electron removed) atoms are accelerated and then passed through a velocity selector consisting of perpendicular electric and magnetic fields. The electric field is 155 V/m and the magnetic field is 0.0315 T. The ions next enter a unif
> A flat, square surface with side length 3.40 cm is in the xy-plane at z = 0. Calculate the magnitude of the flux through this surface produced by a magnetic field
> A particle with charge 7.80 µC is moving with velocity
> An electron experiences a magnetic force of magnitude 4.60 × 10-15 N when moving at an angle of 60.0 with respect to a magnetic field of magnitude 3.50 × 10-3 T. Find the speed of the electron.
> A particle with mass 1.81 × 10-3 kg and a charge of 1.22 × 10-8 C has, at a given instant, a velocity
> A particle with a charge of -1.24 × 10-8 C is moving with instantaneous velocity
> Now the three resistors of Exercise 26.8 are connected in series to the same battery. Answer the same questions for this situation. Exercise 26.8: Three resistors having resistances of 1.60 Ω, 2.40 Ω, and 4.80 Ω are connected in parallel to a 28.0-V ba
> Four, long, parallel power lines each carry 100-A currents. A cross-sectional diagram of these lines is a square, 20.0 cm on each side. For each of the three cases shown in Fig. E28.25, calculate the magnetic field at the center of the square. Fig. E28.
> A 42-Ω resistor and a 20-Ω resistor are connected in parallel, and the combination is connected across a 240-V dc line. (a). What is the resistance of the parallel combination? (b). What is the total current through the parallel combination? (c). What
> A resistor with R1 = 25.0 Ω is connected to a battery that has negligible internal resistance and electrical energy is dissipated by R1 at a rate of 36.0 W. If a second resistor with R2 = 15.0 Ω is connected in series with R1, what is the total rate at w
> Compute the equivalent resistance of the network in Fig. E26.13, and find the current in each resistor. The battery has negligible internal resistance. Fig. E26.13: E = 60.0 V, r = 0 3.00 Ω 12.0 Ω 6.00 Ω 4.00 Ω
> You are to make a resistor by winding a wire around a cylindrical form. To make the inductance as small as possible, it is proposed that you wind half the wire in one direction and the other half in the opposite direction. Would this achieve the desired
> Two closely wound circular coils have the same number of turns, but one has twice the radius of the other. How are the self-inductances of the two coils related? Explain your reasoning.
> In Fig. 30.1, if coil 2 is turned 900 so that its axis is vertical, does the mutual inductance increase or decrease? Explain. Fig. 30.1: Coil 1 N turns Coil 2 N, turns В P82 it
> From Eq. (30.5) 1H = 1 Wb/A, and from Eqs. (30.4) 1H = 1 Ω∙ s. Show that these two definitions are equivalent.
> In an L-R-C series circuit, what criteria could be used to decide whether the system is overdamped or underdamped? For example, could we compare the maximum energy stored during one cycle to the energy dissipated during one cycle? Explain.
> Suppose there is a steady current in an inductor. If you attempt to reduce the current to zero instantaneously by quickly opening a switch, an arc can appear at the switch contacts. Why? Is it physically possible to stop the current instantaneously? Expl
> In the R-L circuit shown in Fig. 30.11, is the current in the resistor always the same as the current in the inductor? How do you know? Fig. 30.11: a b ell L R S2 +
> A rectangular loop with dimensions 4.20 cm by 9.50 cm carries current I. The current in the loop produces a magnetic field at the center of the loop that has magnitude 5.50 × 10-5 T and direction away from you as you view the plane of the loop. What are
> Three resistors having resistances of 1.60 Ω, 2.40 Ω, and 4.80 Ω are connected in parallel to a 28.0-V battery that has negligible internal resistance. Find (a). the equivalent resistance of the combination; (b). the current in each resistor; (c). the
> In the R-L circuit shown in Fig. 30.11, when switch S1 is closed, the potential vac changes suddenly and discontinuously, but the current does not. Explain why the voltage can change suddenly but the current can’t. Fig. 30.11: a b
> In Section 30.5 the relationship i = dq/dt is used in deriving Eq. (30.20). But a flow of current corresponds to a decrease in the charge on the capacitor. Explain, therefore, why this is the correct equation to use in the derivation, rather than i = -dq
> In Section 30.5 Kirchhoff’s loop rule is applied to an L-C circuit where the capacitor is initially fully charged and the equation -L (di/dt) – (q/C) = 0 is derived. But as the capacitor starts to discharge, the current increases from zero. The equation
> In an electric trolley or bus system, the vehicle’s motor draws current from an overhead wire by means of a long arm with an attachment at the end that slides along the overhead wire. A brilliant electric spark is often seen when the attachment crosses a
> An airplane is in level flight over Antarctica, where the magnetic field of the earth is mostly directed upward away from the ground. As viewed by a passenger facing toward the front of the plane, is the left or the right wingtip at higher potential? Doe
> A long, straight conductor passes through the center of a metal ring, perpendicular to its plane. If the current in the conductor increases, is a current induced in the ring? Explain.
> For Eq. (29.6), show that if v is in meters per second, B in teslas, and L in meters, then the units of the right-hand side of the equation are joules per coulomb or volts (the correct SI units for E). Eq. (29.6):
> A type-II superconductor in an external field between Bc1 and Bc2 has regions that contain magnetic flux and have resistance, and also has superconducting regions. What is the resistance of a long, thin cylinder of such material?
> If magnetic monopoles existed, the right-hand side of Eq. (29.20) would include a term proportional to the current of magnetic monopoles. Suppose a steady monopole current is moving in a long straight wire. Sketch the electric field lines that such a cur
> In a two-cell flashlight, the batteries are usually connected in series. Why not connect them in parallel? What possible advantage could there be in connecting several identical batteries in parallel?
> Match the mathematical statements of Maxwell’s equations as given in Section 29.7 to these verbal statements. (a). Closed electric field lines are evidently produced only by changing magnetic flux. (b). Closed magnetic field lines are produced both by
> In an R-C circuit, a resistor, an uncharged capacitor, a dc battery, and an open switch are in series. In an R-L circuit, a resistor, an inductor, a dc battery, and an open switch are in series. Compare the behavior of the current in these circuits (a).
> Can one have a displacement current as well as a conduction current within a conductor? Explain.

