Question: In This problem , graph each of the
In This problem , graph each of the functions using the graphs of functions f and g below.
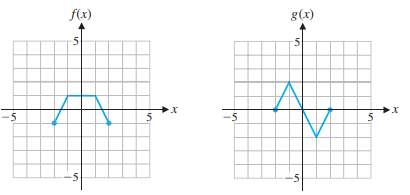
y = 2 ((x)
> Find the vertex form for each quadratic function. Then find each of the following: (A) Intercepts (B) Vertex (C) Maximum or minimum (D) Range g(x) = x2 - 6x + 5
> write an equation for each graph in the form y = a(x – h) 2 + k, where a is either 1 or -1 and h and k are integers.
> write an equation for each graph in the form y = a(x – h) 2 + k, where a is either 1 or -1 and h and k are integers.
> Find each of the following: (A) Intercepts (B) Vertex (C) Maximum or minimum (D) Range n(x) = (x – 4) 2 - 3
> Find each of the following: (A) Intercepts (B) Vertex (C) Maximum or minimum (D) Range g(x) = - (x + 2) 2 + 3
> Find each of the following to the nearest integer by referring to the graphs. (A) Intercepts (B) Vertex (C) Maximum or minimum (D) Range Function g in the figure for Problem 14 Data from Problem 14:
> Find each of the following to the nearest integer by referring to the graphs. (A) Intercepts (B) Vertex (C) Maximum or minimum (D) Range Function m in the figure for Problem 14 Data from Problem 14:
> Find the slope and x intercept of the graph of each equation. 3x + y = 6
> Match each equation with a graph of one of the functions f, g, m, or n in the figure. (A) y = (x – 3)2 - 4 (B) y = - (x + 3)2 + 4 (C) y = - (x – 3)2 + 4 (D) y = (x + 3)2 - 4
> write a brief verbal description of the relationship between the graph of the indicated function and the graph of y = x2 . n(x) = -x2 + 8x - 9
> write a brief verbal description of the relationship between the graph of the indicated function and the graph of y = x2 . g(x) = x2 - 2x - 5
> In This problem , graph each of the functions using the graphs of functions f and g below. y = g(x – 1)
> In This problem , graph each of the functions using the graphs of functions f and g below. y = g(x) - 1
> Find the domain and range of each function.
> Find the domain and range of each function.
> Find the domain and range of each function.
> Find the domain and range of each function.
> Find the domain and range of each function.
> write the solution set using interval notation. -8 < -4x ( 12
> A production analyst has found that on average it takes a new person T(x) minutes to perform a particular assembly operation after x performances of the operation, where (A) Describe how the graph of function T can be obtained from the graph of one of t
> The average weight of a particular species of snake is given by w(x) = 463x3 , 0.2 ( x ( 0.8, where x is length in meters and w(x) is weight in grams. (A) Describe how the graph of function w can be obtained from the graph of one of the basic functions
> Table 6 shows state income tax rates for individuals filing a return in Louisiana. (A) Write a piecewise definition for T(x), the tax due on a taxable income of x dollars. (B) Graph T(x). (C) Find the tax due on a taxable income of $32,000. Of $64,000
> Table 4 shows the electricity rates charged by Monroe Utilities in the winter months. (A) Write a piecewise definition of the monthly charge w(x) for a customer who uses x kWh in a winter month. (B) Graph w(x).
> A company manufactures and sells in-line skates. Its financial department has established the price– demand function p1x2 = 190 - 0.0131x - 102 2 10 … x … 100 where p1x2 is the price at which x thousand pairs of in-line skates can be sold. (A) Describe h
> The manufacturer of the bicycle helmets is willing to supply x helmets at a price of p(x) as given by the equation p(x) = 4√x 9 ( x ( 289 (A) Describe how the graph of function p can be obtained from the graph of one of the basic funct
> Changing the order in a sequence of transformations may change the final result. Investigate each pair of transformations in this Problem to determine if reversing their order can produce a different result. Support your conclusions with specific example
> Changing the order in a sequence of transformations may change the final result. Investigate each pair of transformations in this Problem to determine if reversing their order can produce a different result. Support your conclusions with specific example
> Changing the order in a sequence of transformations may change the final result. Investigate each pair of transformations in this Problem to determine if reversing their order can produce a different result. Support your conclusions with specific example
> Graph involve a reflection in the x axis and/or a vertical stretch or shrink of one of the basic functions in Figure 1 on page 58. Identify the basic function, and describe the transformation verbally. Write an equation for the given graph. Figure-1:
> Find the slope and x intercept of the graph of each equation. y = -4x + 12
> Graph involve a reflection in the x axis and/or a vertical stretch or shrink of one of the basic functions in Figure 1 on page 58. Identify the basic function, and describe the transformation verbally. Write an equation for the given graph. Figure-1:
> Graph involve a reflection in the x axis and/or a vertical stretch or shrink of one of the basic functions in Figure 1 on page 58. Identify the basic function, and describe the transformation verbally. Write an equation for the given graph. Figure-1:
> Graph each function.
> Graph each function.
> Graph each function.
> The graph of the function g is formed by applying the indicated sequence of transformations to the given function f. Find an equation for the function g and graph g using -5 ( x ( 5 and -5 ( y ( 5. The graph of ƒ(x)= x2 is reflected in the x axis and shi
> The graph of the function g is formed by applying the indicated sequence of transformations to the given function f. Find an equation for the function g and graph g using -5 ( x ( 5 and -5 ( y ( 5. The graph of ƒ(x)= | x | is reflected in the x axis and
> The graph of the function g is formed by applying the indicated sequence of transformations to the given function f. Find an equation for the function g and graph g using -5 ( x ( 5 and -5 ( y ( 5.
> Graph in this Problem is the result of applying a sequence of transformations to the graph of one of the six basic functions in Figure 1 on page 58. Identify the basic function and describe the transformation verbally. Write an equation for the given gra
> Graph in this Problem is the result of applying a sequence of transformations to the graph of one of the six basic functions in Figure 1 on page 58. Identify the basic function and describe the transformation verbally. Write an equation for the given gra
> write the solution set using interval notation 3x ( 12
> Graph in this Problem is the result of applying a sequence of transformations to the graph of one of the six basic functions in Figure 1 on page 58. Identify the basic function and describe the transformation verbally. Write an equation for the given gra
> Graph in this Problem is the result of applying a sequence of transformations to the graph of one of the six basic functions in Figure 1 on page 58. Identify the basic function and describe the transformation verbally. Write an equation for the given gra
> Describe how the graph of each function is related to the graph of one of the six basic functions in Figure 1 on page 58. Sketch a graph of each function. m(x) = –0.4x2 is
> Describe how the graph of each function is related to the graph of one of the six basic functions in Figure 1 on page 58. Sketch a graph of each function. /
> Describe how the graph of each function is related to the graph of one of the six basic functions in Figure 1 on page 58. Sketch a graph of each function. m(x) = (x + 3)2 + 4
> Describe how the graph of each function is related to the graph of one of the six basic functions in Figure 1 on page 58. Sketch a graph of each function. h (x) = - | x - 5 |
> In This problem , graph each of the functions using the graphs of functions f and g below. y = - (0.5g (x) + 3
> In This problem , graph each of the functions using the graphs of functions f and g below. y = -0.5g (x) + 3
> In This problem , graph each of the functions using the graphs of functions f and g below. y = -g (x)
> Find the slope and y intercept of the graph of each equation.
> In This problem , graph each of the functions using the graphs of functions f and g below. y = ((x) + 3
> In This problem , graph each of the functions using the graphs of functions f and g below. y = ( (x + 3)
> Indicate whether table specifies a function.
> Use point-by-point plotting to sketch the graph of each equation. xy = 12
> Use point-by-point plotting to sketch the graph of each equation. x = y3
> Use point-by-point plotting to sketch the graph of each equation. y = x2
> Use point-by-point plotting to sketch the graph of each equation. x = y + 1
> The percentage s of seats in the House of Representatives won by Democrats and the percentage v of votes cast for Democrats (when expressed as decimal fractions) are related by the equation 5v - 2s = 1.4 0 < s < 1, 0.28 < v < 0.68 (A) Express v a
> The financial department for the company in Problems 86 and 88 established the following cost function for producing and selling x thousand notebook computers: C1x2 = 4,000 + 500x thousand dollars (A) Write a profit function for producing and selling x
> (A) Using the price–demand function P(x) = 2,000 - 60x 1 ( x ( 25 from Problem 86, write the company’s revenue function and indicate its domain. (B) Complete Table 11, computing revenues to the nearest thousand
> write the solution set using interval notation -1 ( x < 5
> A company manufactures notebook computers. Its marketing research department, using statistical techniques, collected the data shown in Table 9, where p is the wholesale price per computer at which x thousand computers can be sold. Using special analytic
> Refer to the area A and perimeter P of a rectangle with length l and width w (see the figure). The perimeter of a rectangle is 160 m. Express the area A1w2 as a function of the width w, and state the domain of this function.
> Refer to the area A and perimeter P of a rectangle with length l and width w (see the figure). The area of a rectangle is 81 sq in. Express the perimeter P1l2 as a function of the length l, and state the domain of this function
> Find and simplify each of the following, assuming h (( 0 in (C). ƒ(x ) = x ( x + 40 )
> Find and simplify each of the following, assuming h (( 0 in (C). ƒ(x ) = 3x2 + 5x - 8
> Find and simplify each of the following, assuming h (( 0 in (C). ƒ(x ) = -3x + 9
> Find and simplify the expression if ƒ(x) = x2 - 4. ƒ( -3 + h ) - ƒ( -3 )
> Find and simplify the expression if ƒ(x) = x2 - 4. ƒ( -3 + h )
> Find and simplify the expression if ƒ(x) = x2 - 4. ƒ(-3) + ƒ(h)
> Find and simplify the expression if ƒ(x) = x2 - 4. ƒ(∜x)
> Find the slope and y intercept of the graph of each equation.
> Find and simplify the expression if ƒ(x) = x2 - 4. ƒ(x3)
> Find and simplify the expression if ƒ(x) = x2 - 4. ƒ(x - 1)
> Find and simplify the expression if ƒ(x) = x2 - 4. ƒ(-3x)
> Does the equation specify a function with independent variable x? If so, find the domain of the function. If not, find a value of x to which there corresponds more than one value of y.
> Does the equation specify a function with independent variable x? If so, find the domain of the function. If not, find a value of x to which there corresponds more than one value of y. x2 + y2 = 9
> Does the equation specify a function with independent variable x? If so, find the domain of the function. If not, find a value of x to which there corresponds more than one value of y. X (x + y) = 4
> Does the equation specify a function with independent variable x? If so, find the domain of the function. If not, find a value of x to which there corresponds more than one value of y. 6x - 7y = 21
> Find the domain of each function.
> Find the domain of each function.
> Find the domain of each function. H(x) = 7 - 2x2 - x4
> write the interval as an inequality or double inequality. [ 9 , ∞ )
> Use the following graph of a function f to determine x or y to the nearest integer, as indicated. Æ’(x) = 0
> Use the following graph of a function f to determine x or y to the nearest integer, as indicated. Æ’(x) = 4
> Use the following graph of a function f to determine x or y to the nearest integer, as indicated. y = Æ’(-2)
> Use the following graph of a function f to determine x or y to the nearest integer, as indicated. y = Æ’(4)
> The three points in the table are on the graph of the indicated function f. Do these three points provide sufficient information for you to sketch the graph of y = Æ’(x) ? Add more points to the table until you are satisfied that your sketch i
> use point-by-point plotting to sketch the graph of each function.
> use point-by-point plotting to sketch the graph of each function. ƒ(x)= x3 - 2
> use point-by-point plotting to sketch the graph of each function. ƒ(x) = 3 - x2
> use point-by-point plotting to sketch the graph of each function.
> Equation specifies a function with independent variable x. Determine whether the function is linear, constant, or neither.
> Find the slope and y intercept of the graph of each equation. y = 3x + 2
> solve for x 7x - 6 = 5x - 24
> If a contingent liability is probable but estimable only within a range, what amount, if any, should the firm report?
> Suppose the firm’s analysis of a contingent liability indicates that an obligation is not probable. What accounting treatment, if any, is warranted?
> Under what circumstances should a firm report a contingent liability?
> List and briefly describe the three categories of likelihood that a payment for a contingent liability will need to be made.

