Question: Interference effects are produced at point P
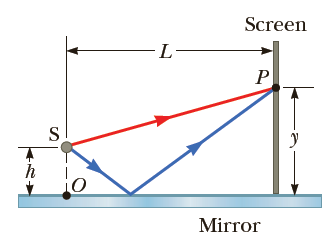
Interference effects are produced at point P on a screen as a result of direct rays from a 5.00 x 102 - nm source and reflected rays off a mirror, as shown in Figure P24.67. If the source is L = 1.00 x 102 m to the left of the screen and h = 1.00 cm above the mirror, find the distance y (in millimeters) to the first dark band above the mirror.
Figure P24.67:
> You are pulling a suitcase through the airport at a constant speed by exerting a force of 25.0 N at angle 30.0° from the vertical. What is the force of friction acting on the suitcase?
> (a) What assumptions do you make when you call the reading of a bathroom scale your “weight”? What does the scale really tell you? (b) Under what circumstances might the reading of the scale not be equal to your weight?
> An 85 kg skier is sliding down a ski slope at a constant velocity. The slope makes an angle of 11° above the horizontal direction. Ignore air resistance. (a) What is the force of kinetic friction acting on the skier? (b) What is the coefficient of kineti
> An 80.0 N crate of apples sits at rest on a ramp that runs from the ground to the bed of a truck. The ramp is inclined at 20.0° to the ground. (a) What is the normal force exerted on the crate by the ramp? (b) The interaction partner of this normal for
> Mechanical advantage is the ratio of the force required without the use of a simple machine to that needed when using the simple machine. Compare the force to lift an object with that needed to slide the same object up a frictionless incline and show tha
> (a) In Example 2.14, if the movers stop pushing on the safe, can static friction hold the safe in place without having it slide back down? (b) If not, what minimum force needs to be applied to hold the safe in place?
> Before hanging new William Morris wallpaper in her bedroom, Brenda sanded the walls lightly to smooth out some irregularities on the surface. The sanding block weighs 2.0 N and Brenda pushes on it with a force of 3.0 N at an angle of 30.0° with respect t
> A crate of artichokes is on a ramp that is inclined 10.0° above the horizontal. Give the direction of the normal force and the friction force acting on the crate in each of these situations. (a) The crate is at rest. (b) The crate is sliding up the ramp.
> A crate of potatoes of mass 18.0 kg is on a ramp with angle of incline 30° to the horizontal. The coefficients of friction are μs = 0.75 and μk = 0.40. Find the normal force (magnitude) and the frictional force (magnitude and direction) on the crate if t
> A crate of potatoes of mass 18.0 kg is on a ramp with angle of incline 30° to the horizontal. The coefficients of friction are μs = 0.75 and μk = 0.40. Find the normal force (magnitude) and the frictional force (magnitude and direction) on the crate if t
> A crate of potatoes of mass 18.0 kg is on a ramp with angle of incline 30° to the horizontal. The coefficients of friction are μs = 0.75 and μk = 0.40. Find the normal force (magnitude) and the frictional force (magnitude and direction) on the crate if t
> A crate of potatoes of mass 18.0 kg is on a ramp with angle of incline 30° to the horizontal. The coefficients of friction are μs = 0.75 and μk = 0.40. Find the normal force (magnitude) and the frictional force (magnitude and direction) on the crate if t
> (a) Is it possible for the sum of two vectors to be smaller in magnitude than the magnitude of either vector? (b) Is it possible for the magnitude of the sum of two vectors to be larger than the sum of the magnitudes of the vectors?
> A person is standing on a bathroom scale. Which of the following is not a force exerted on the scale: a contact force due to the floor, a contact force due to the person's feet, the weight of the person, the weight of the scale?
> When sodium is bombarded with electrons accelerated through a potential difference ΔV, its x - ray spectrum contains emission peaks at 1.04 keV and 1.07 keV. Find the minimum value of ΔV required to produce both of these peaks.
> What minimum accelerating voltage is required to produce an x - ray with a wavelength of 70.0 pm?
> Calculate the minimum - wavelength x - ray that can be produced when a target is struck by an electron that has been accelerated through a potential difference of (a) 15.0 kV and (b) 1.00 x 102 kV. (c) What happens to the minimum wavelength as the potent
> The extremes of the x - ray portion of the electromagnetic spectrum range from approximately 1.0 x 10-8 m to 1.0 x 10-13 m. Find the minimum accelerating voltages required to produce wavelengths at these two extremes.
> Two light sources are used in a photoelectric experiment to determine the work function for a particular metal surface. When green light from a mercury lamp (λ = 546.1 nm) is used, a stopping potential of 0.376 V reduces the photocurrent to zero. (a) Bas
> When monochromatic light of an unknown wavelength falls on a sample of silver, a minimum potential of 2.50 V is required to stop all of the ejected photoelectrons. Determine the (a) Maximum kinetic energy and (b) Maximum speed of the ejected photoelectro
> Lithium, beryllium, and mercury have work functions of 2.30 eV, 3.90 eV, and 4.50 eV, respectively. Light with a wavelength of 4.00 x 102 nm is incident on each of these metals. (a) Which of these metals emit photoelectrons in response to the light? Why?
> The work function for platinum is 6.35 eV. (a) Convert the value of the work function from electron volts to joules. (b) Find the cutoff frequency for platinum. (c) What maximum wavelength of light incident on platinum releases photoelectrons from the pl
> The work function for zinc is 4.31 eV. (a) Find the cutoff wavelength for zinc. (b) What is the lowest frequency of light incident on zinc that releases photoelectrons from its surface? (c) If photons of energy 5.50 eV are incident on zinc, what is the m
> When light of wavelength 3.50 x 102 nm falls on a potassium surface, electrons having a maximum kinetic energy of 1.31 eV are emitted. Find (a) The work function of potassium, (b) The cutoff wavelength, and (c) The frequency corresponding to the cutoff w
> Monochromatic light falls on a screen 1.75 m from two slits separated by 2.10 mm. The first - and second - order bright fringes are separated by 0.552 mm. What is the wavelength of the light?
> The threshold of dark - adapted (scotopic) vision is 4.0 x 10-11 W/m2 at a central wavelength of 5.00 x 102 nm. If light with this intensity and wavelength enters the eye when the pupil is open to its maximum diameter of 8.5 mm, how many photons per seco
> Calculate the energy, in electron volts, of a photon whose frequency is (a) 6.20 x 102 THz, (b) 3.10 GHz, and (c) 46.0 MHz.
> Suppose a star with radius 8.50 x 108 m has a peak wavelength of 685 nm in the spectrum of its emitted radiation. (a) Find the energy of a photon with this wavelength. (b) What is the surface temperature of the star? (c) At what rate is energy emitted fr
> Earth’s average surface temperature is about 287 K. Assuming Earth radiates as a blackbody, calculate λmax for the Earth.
> The radius of our Sun is 6.96 x 108 m, and its total power output is 3.85 x 1026 W. (a) Assuming the Sun’s surface emits as a blackbody, calculate its surface temperature. (b) Using the result of part (a), find λmax for the Sun.
> The temperature of a student’s skin is 33.0°C. At what wavelength does the radiation emitted from the skin reach its peak?
> (a) Lightning produces a maximum air temperature on the order of 104 K, whereas (b) A nuclear explosion produces a temperature on the order of 107 K. Use Wien’s displacement law to find the order of magnitude of the wavelength of the thermally produced p
> Why is it impossible to simultaneously measure the position and velocity of a particle with infinite accuracy?
> Why is an electron microscope more suitable than an optical microscope for “seeing” objects of atomic size?
> If matter has a wave nature, why is this wave - like characteristic not observable in our daily experiences?
> Light of wavelength 6.0 x 102 nm falls on a double slit, and the first bright fringe of the interference pattern is observed to make an angle of 12° with the horizontal. Find the separation between the slits.
> The atoms in a crystal lie in planes separated by a few tenths of a nanometer. Can a crystal be used to produce a diffraction pattern with visible light as it does for x - rays? Explain your answer with reference to Bragg’s law.
> The brightest star in the constellation Lyra is the bluish star Vega, whereas the brightest star in Boötes is the reddish star Arcturus. How do you account for the difference in color of the two stars?
> What effect, if any, would you expect the temperature of a material to have on the ease with which electrons can be ejected from it via the photoelectric effect?
> Which has more energy, a photon of ultraviolet radiation or a photon of yellow light?
> Is light a wave or a particle? Support your answer by citing specific experimental evidence.
> A flat piece of glass is supported horizontally above the flat end of a 10.0 - cm - long metal rod that has its lower end rigidly fixed. The thin film of air between the rod and the glass is observed to be bright when illuminated by light of wavelength 5
> A diffraction pattern is produced on a screen 1.40 m from a single slit, using monochromatic light of wavelength 5.00 x 102 nm. The distance from the center of the central maximum to the first - order maximum is 3.00 mm. Calculate the slit width. Assume
> A plano - convex lens (flat on one side, convex on the other) with index of refraction n rests with its curved side (radius of curvature R) on a flat glass surface of the same index of refraction with a film of index nfilm between them. The lens is illum
> The transmitting antenna on a submarine is 5.00 m above the water when the ship surfaces. The captain wishes to transmit a message to a receiver on a 90.0 - m - tall cliff at the ocean shore. If the signal is to be completely polarized by reflection off
> Three polarizers, centered on a common axis and with their planes parallel to one another, have transmission axes oriented at angles of θ1, θ2, and θ3 from the vertical, as shown in Figure P24.59. Light of intensity
> Two radio antennas separated by d = 3.00 x 102 m, as shown in Figure P24.7, simultaneously broadcast identical signals at the same wavelength. A car travels due north along a straight line at position x = 1.00 x 103 m from the center point between the an
> Figure P24.69 shows a radio - wave transmitter and a receiver, both h = 50.0 m above the ground and d = 6.00 x 102 m apart. The receiver can receive signals directly from the transmitter and indirectly from signals that bounce off the ground. If the grou
> Many cells are transparent and colorless. Structures of great interest in biology and medicine can be practically invisible to ordinary microscopy. An interference microscope reveals a difference in refractive index as a shift in interference fringes to
> The two speakers are placed 35.0 cm apart. A single oscillator makes the speakers vibrate in phase at a frequency of 2.00 kHz. At what angles, measured from the perpendicular bisector of the line joining the speakers, would a distant observer hear maximu
> Light of wavelength 546 nm (the intense green line from a mercury source) produces a Young’s interference pattern in which the second minimum from the central maximum is along a direction that makes an angle of 18.0 min of arc with the axis through the c
> In a Young’s interference experiment, the two slits are separated by 0.150 mm and the incident light includes two wavelengths: λ1 = 5.40 x 102 nm (green) and λ2 = 4.50 x 102 nm (blue). The overlapping interference patterns are observed on a screen 1.40 m
> Laser light with a wavelength of 632.8 nm is directed through one slit or two slits and allowed to fall on a screen 2.60 m beyond. Figure P24.63 shows the pattern on the screen, with a centimeter ruler below it. Did the light pass through one slit or two
> Light from a helium–neon laser (λ = 632.8 nm) is incident on a single slit. What is the maximum width of the slit for which no diffraction minima are observed?
> Light with a wavelength in vacuum of 546.1 nm falls perpendicularly on a biological specimen that is 1.000 μm thick. The light splits into two beams polarized at right angles, for which the indices of refraction are 1.320 and 1.333, respectively. (a) Cal
> Light of intensity I0 is polarized vertically and is incident on an analyzer rotated at an angle θ from the vertical. Find the angle θ if the transmitted light has intensity (a) I = (0.750)I0, (b) I = (0.500)I0, (c) I = (0.250)I0, and (d) I = 0.
> A double slit separated by 0.058 0 mm is placed 1.50 m from a screen. (a) If yellow light of wavelength 588 nm strikes the double slit, what is the separation between the zeroth - order and first - order maxima on the screen? (b) If blue light of wavelen
> Three polarizing plates whose planes are parallel are centered on a common axis. The directions of the transmission axes relative to the common vertical direction are shown in Figure P24.59. A linearly polarized beam of light with plane of polarization p
> Plane - polarized light is incident on a single polarizing disk, with the direction of E0 parallel to the direction of the transmission axis. Through what angle should the disk be rotated so that the intensity in the transmitted beam is reduced by a fact
> Equation 24.14 assumes the incident light is in air. If the light is incident from a medium of index n1 onto a medium of index n2, follow the procedure used to derive Equation 24.14 to show that tan θp = n2/n1.
> The critical angle for total internal reflection for sapphire surrounded by air is 34.4°. Calculate the Brew ster’s angle for sapphire if the light is incident from the air.
> A light beam is incident on a piece of fused quartz (n = 1.458) at the Brewster’s angle. Find a) The value of Brewster’s angle and (b) The angle of refraction for the transmitted ray.
> At what angle above the horizon is the Sun if light from it is completely polarized upon reflection from water?
> The index of refraction of a glass plate is 1.52. What is the Brewster’s angle when the plate is (a) In air and (b) In water?
> Unpolarized light passes through two Polaroid sheets. The transmission axis of the analyzer makes an angle of 35.0° with the axis of the polarizer. (a) What fraction of the original unpolarized light is transmitted through the analyzer? (b) What fraction
> The angle of incidence of a light beam in air onto a reflecting surface is continuously variable. The reflected ray is found to be completely polarized when the angle of incidence is 48.0°. (a) What is the index of refraction of the reflecting material?
> Light containing two different wavelengths passes through a diffraction grating with 1.20 x 103 slits/cm. On a screen 15.0 cm from the grating, the third - order maximum of the shorter wavelength falls midway between the central maximum and the first sid
> In a location where the speed of sound is 354 m/s, a 2.00 kHz sound wave impinges on two slits 30.0 cm apart. (a) At what angle is the first maximum located? (b) If the sound wave is replaced by 3.00 - cm microwaves, what slit separation gives the same a
> Light of wavelength 5.00 x 102 nm is incident normally on a diffraction grating. If the third - order maximum of the diffraction pattern is observed at 32.0°, (a) What is the number of rulings per centimeter for the grating? (b) Determine the total numbe
> Monochromatic light at 577 nm illuminates a diffraction grating with 325 lines/mm. Determine (a) The angle to the first - order maximum, (b) The highest order that can be observed with this grating at the given wavelength, and (c) The angle to this highe
> Sunlight is incident on a diffraction grating that has 2750 lines/ cm. The second - order spectrum over the visible range (400.– 700. nm) is to be limited to 1.75 cm along a screen that is a distance L from the grating. What is the required value of L?
> White light is incident on a diffraction grating with 475 lines/ mm. (a) Calculate the angle θr2 to the second - order maximum for a wavelength of 675 nm. (b) Calculate the wavelength of light with a third - order maximum at the same angle θr2.
> Light from an argon laser strikes a diffraction grating that has 5310 grooves/cm. The central and first - order principal maxima are separated by 0.488 m on a wall 1.72 m from the grating. Determine the wavelength of the laser light.
> White light is spread out into its spectral components by a diffraction grating. If the grating has 2.00 x 103 lines/cm, at what angle does red light of wavelength 6.40 x 102 nm appear in the first - order spectrum?
> A helium–neon laser (λ = 632.8 nm) is used to calibrate a diffraction grating. If the first - order maximum occurs at 20.5°, what is the spacing between adjacent grooves in the grating?
> Consider an array of parallel wires with uniform spacing of 1.30 cm between centers. In air at 20.0°C, ultrasound with a frequency of 37.2 kHz from a distant source is incident perpendicular to the array. (Take the speed of sound to be 343 m/s.) (a) Find
> The hydrogen spectrum has a red line at 656 nm and a violet line at 434 nm. What angular separations between these two spectral lines can be obtained with a diffraction grating that has 4.50 x 103 lines/cm?
> Intense white light is incident on a diffraction grating that has 600. lines/mm. (a) What is the highest order in which the complete visible spectrum can be seen with this grating? (b) What is the angular separation between the violet edge (400. nm) and
> Light of wavelength 620. nm falls on a double slit, and the first bright fringe of the interference pattern is seen at an angle of 15.0° from the central maximum. Find the separation between the slits.
> Three discrete spectral lines occur at angles of 10.1°, 13.7°, and 14.8°, respectively, in the first - order spectrum of a diffraction - grating spectrometer. (a) If the grating has 3660 slits/cm, what are the wavelengths of the light? (b) At what angles
> The second - order dark fringe in a single - slit diffraction pattern is 1.40 mm from the center of the central maximum. Assuming the screen is 85.0 cm from a slit of width 0.800 mm and assuming monochromatic incident light, calculate the wavelength of t
> A slit of width 0.50 mm is illuminated with light of wavelength 5.00 x 102 nm, and a screen is placed 1.20 x 102 cm in front of the slit. Find the widths of the first and second maxima on each side of the central maximum.
> A screen is placed 50.0 cm from a single slit that is illuminated with light of wavelength 6.80 x 102 nm. If the distance between the first and third minima in the diffraction pattern is 3.00 mm, what is the width of the slit?
> A beam of monochromatic light is diffracted by a slit of width 0.600 mm. The diffraction pattern forms on a wall 1.30 m beyond the slit. The width of the central maximum is 2.00 mm. Calculate the wavelength of the light.
> Microwaves of wavelength 5.00 cm enter a long, narrow window in a building that is otherwise essentially opaque to the incoming waves. If the window is 36.0 cm wide, what is the distance from the central maximum to the first - order minimum along a wall
> Light of wavelength 587.5 nm illuminates a slit of width 0.75 mm. (a) At what distance from the slit should a screen be placed if the first minimum in the diffraction pattern is to be 0.85 mm from the central maximum? (b) Calculate the width of the centr
> A student and his lab partner create a single slit by carefully aligning two razor blades to a separation of 0.500 mm. When a helium–neon laser at 633 nm illuminates the slit, a diffraction pattern is observed on a screen 1.25 m beyond the slit. Calculat
> Light of wavelength 5.40 x 102 nm passes through a slit of width 0.200 mm. (a) Find the width of the central maximum on a screen located 1.50 m from the slit. (b) Determine the width of the first - order bright fringe.
> A lens made of glass (ng = 1.52) is coated with a thin film of MgF2 (ns = 1.38) of thickness t. Visible light is incident normally on the coated lens as in Figure P24.30. (a) For what minimum value of t will the reflected light of wavelength 5.40 x 102 n
> Light at 633 nm from a helium–neon laser shines on a pair of parallel slits separated by 1.45 x 10-5 m and an interference pattern is observed on a screen 2.00 m from the plane of the slits. (a) Find the angle from the central maximum to the first bright
> A thin film of glycerin (n = 1.473) of thickness 524 nm with air on both sides is illuminated with white light at near normal incidence. What wavelengths will be strongly reflected in the range 300 nm to 700 nm?
> Nonreflective coatings on camera lenses reduce the loss of light at the surfaces of multi-lens systems and prevent internal reflections that might mar the image. Find the minimum thickness of a layer of magnesium fluoride (n = 1.38) on flint glass (n = 1
> A thin film of oil (n = 1.45) of thickness 425 nm with air on both sides is illuminated with white light at normal incidence. Determine (a) The most strongly and (b) The most weakly reflected wavelengths in the range 400 nm to 600 nm.
> A plano - convex lens with radius of curvature R = 3.0 m is in contact with a flat plate of glass. A light source and the observer’s eye are both close to the normal, as shown in Figure 24.10a. The radius of the 50th bright Newtonâ
> An investigator finds a fiber at a crime scene that he wishes to use as evidence against a suspect. He gives the fiber to a technician to test the properties of the fiber. To measure the diameter of the fiber, the technician places it between two flat gl
> A spacer is cut from a playing card of thickness 2.90 x 10-4 m and used to separate one end of two rectangular, optically flat, 3.00 - cm long glass plates with n = 1.55, as in Figure P24.24. Laser light at 594 nm shines straight down on the top plate. T
> Astronomers observe the chromosphere of the Sun with a filter that passes the red hydrogen spectral line of wavelength 656.3 nm, called the Hα line. The filter consists of a transparent dielectric of thickness d held between two partially aluminized glas
> An oil film (n = 1.45) floating on water is illuminated by white light at normal incidence. The film is 2.80 x 102 nm thick. Find (a) The wavelength and color of the light in the visible spectrum most strongly reflected and (b) The wavelength and color o
> A possible means for making an airplane invisible to radar is to coat the plane with an antireflective polymer. If radar waves have a wavelength of 3.00 cm and the index of refraction of the polymer is n = 1.50, how thick would you make the coating? Assu
> Krypton (atomic number 36) has how many electrons in its next - to - outer shell (n = 3)? (a) 2 (b) 4 (c) 8 (d) 18

