Question: Let 5 be the region that lies
Let 5 be the region that lies between the curves
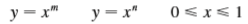
where m and n are integers with 0 (a) Sketch the region /.
(b) Find the coordinates of the centroid of /.
(c) Try to find values of m and n such that the centroid lies outside /.
Transcribed Image Text:
y = x" y = x" 0 < x< 1
> Find the exact length of the curve. y = In(cos x), 0 <x</3 %3|
> Find the exact length of the curve. 3 Vy (у — 3), 1<y<9
> Find a power series representation for the function and determine the interval of convergence. 1 1+ x S(x)
> Find the exact length of the curve. 1 1<y<2 8 4y² +
> Find the exact length of the curve. 1<x<2 y = 3 4x +
> Find the exact length of the curve. 36y? = (x² – 4), 2<x<3, y > 0 %3D
> Find the exact length of the curve. y = 1 + 6x2, 0<x<1 3/2
> Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. y? = In x, -1 < y< 1
> Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. x= Vy - y, 1< y< 4 X =
> Set up an integral that represents the length of the curve. Then use your calculator to find the length correct to four decimal places. y = xe, 0<I<2
> Use the arc length formula to find the length of the curve / Check your answer by noting that the curve is part of a circle.
> Use the arc length formula (3) to find the length of the curve y = 2x - 5, 21 < x < 3. Check your answer by noting that the curve is a line segment and calculating its length by the distance formula.
> Formula 4 is valid only when f(x) > 0. Show that when f(x) is not necessarily positive, the formula for surface area becomes s = [" 27| f(x)|/T +[S(x)F dx
> Let L be the length of the curve y = f(x), a < x < b, where f is positive and has a continuous derivative. Let Sf be the surface area generated by rotating the curve about the x axis. If c is a positive constant, define t(x) = f(x) 1 c and let St be the
> Show that if we rotate the curve y = ex/2 + ex/2 about the x axis, the area of the resulting surface is the same value as the enclosed volume for any interval a < x < b.
> Find the area of the surface obtained by rotating the circle x2 + y2 = r2 about the line y = r.
> Use the result of Exercise 33 to set up an integral to find the area of the surface generated by rotating the curve / 0 < x < 4, about the line y = 4. Then use a CAS to evaluate the integral. Data from Exercise 33: If the curve y = f(x), a < x < b, is
> If the curve y = f(x), a < x < b, is rotated about the horizontal line y = c, where f(x) < c, find a formula for the area of the resulting surface.
> Find the surface area of the torus in Exercise 6.2.63. Data from Exercise 6.2.63: (a) Set up an integral for the volume of a solid torus (the donut-shaped solid shown in the figure) with radii r and R. (b) By interpreting the integral as an area, find
> A group of engineers is building a parabolic satellite dish whose shape will be formed by rotating the curve y = ax2 about the y axis. If the dish is to have a 10ft diameter and a maximum depth of 2 ft, find the value of a and the surface area of the d
> (a) If a > 0, find the area of the surface generated by rotating the loop of the curve 3ay2 = x (a - x)2 about the x axis. (b) Find the surface area if the loop is rotated about the y axis.
> If the infinite curve y = ex, x > 0, is rotated about the x axis, find the area of the resulting surface.
> Use a CAS to find the exact area of the surface obtained by rotating the curve about the y axis. If your CAS has trouble evaluating the integral, express the surface area as an integral in the other variable. у — In(x + 1), 0 <x<1 y
> Use a CAS to find the exact area of the surface obtained by rotating the curve about the y­ axis. If your CAS has trouble evaluating the integral, express the surface area as an integral in the other variable. y = x', 0< y< 1
> Use either a CAS or a table of integrals to find the exact area of the surface obtained by rotating the given curve about the x­ axis y = Vx? + 1, 0<x<3
> Use either a CAS or a table of integrals to find the exact area of the surface obtained by rotating the given curve about the x­ axis. y = 1/x, 1<x< 2
> Use Simpson’s Rule with n = 10 to approximate the area of the surface obtained by rotating the curve about the x axis. Compare your answer with the value of the integral produced by a calculator. y = x In x, 1 r< 2
> Use Simpson’s Rule with n = 10 to approximate the area of the surface obtained by rotating the curve about the x axis. Compare your answer with the value of the integral produced by a calculator. y = xe", 0 < x<1
> Use Simpson’s Rule with n = 10 to approximate the area of the surface obtained by rotating the curve about the x axis. Compare your answer with the value of the integral produced by a calculator. y = x + x², 0<x<1
> Use Simpson’s Rule with n = 10 to approximate the area of the surface obtained by rotating the curve about the x­ axis. Compare your answer with the value of the integral produced by a calculator. y = x', 0< x < 5
> The given curve is rotated about the y axis. Find the area of the resulting surface. y = x' - } In x, 1 < x< 2
> The given curve is rotated about the y axis. Find the area of the resulting surface. x = Va? – y², 0 <y<a/2
> The given curve is rotated about the y axis. Find the area of the resulting surface. x2/3 + y/3 = 1, 0< y<1 %3|
> The given curve is rotated about the y­ axis. Find the area of the resulting surface. y = }x2, 0 <x< 12
> Find the exact area of the surface obtained by rotating the curve about the x axis. x = 1 + 2y?, 1 <y<2
> Find the exact area of the surface obtained by rotating the curve about the x axis. x = }(y² + 2)/², 1<y<2 + 2)/2, ミys2
> Find the exact area of the surface obtained by rotating the curve about the x axis. y = 6. 2x
> Find the exact area of the surface obtained by rotating the curve about the x axis. y = cos(}x), 0<x<T
> Find the exact area of the surface obtained by rotating the curve about the x axis. y = V1 + e*, 0<x<1
> Find the exact area of the surface obtained by rotating the curve about the x axis. y² = x + 1, 0<x< 3
> Find the exact area of the surface obtained by rotating the curve about the x axis. у3 V5 — х, 3<x<5
> Find the exact area of the surface obtained by rotating the curve about the x­ axis. y = x', 0< x < 2
> (a) Set up an integral for the area of the surface obtained by rotating the curve about (i) the x axis and (ii) the y axis. (b) Use the numerical integration capability of a calculator to evaluate the surface areas correct to four decimal places. у —
> (a) Set up an integral for the area of the surface obtained by rotating the curve about (i) the x axis and (ii) the y axis. (b) Use the numerical integration capability of a calculator to evaluate the surface areas correct to four decimal places. x =
> (a) Set up an integral for the area of the surface obtained by rotating the curve about (i) the x axis and (ii) the y axis. (b) Use the numerical integration capability of a calculator to evaluate the surface areas correct to four decimal places. x =
> (a) Set up an integral for the area of the surface obtained by rotating the curve about (i) the x axis and (ii) the y axis. (b) Use the numerical integration capability of a calculator to evaluate the surface areas correct to four decimal places. y =
> (a) Set up an integral for the area of the surface obtained by rotating the curve about (i) the x axis and (ii) the y axis. (b) Use the numerical integration capability of a calculator to evaluate the surface areas correct to four decimal places. y =
> (a) Set up an integral for the area of the surface obtained by rotating the curve about (i) the x­ axis and (ii) the y­ axis. (b) Use the numerical integration capability of a calculator to evaluate the surface areas correct to four
> Evaluate the integral using integration by parts with the indicated choices of u and dv. хе ^ dx; и —х, dv — — х, do — e 2* dx
> Use the Second Theorem of Pappus described in Exercise 48 to find the surface area of the torus in Example 7.
> The Second Theorem of Pappus is in the same spirit as Pappus’s Theorem on page 565, but for surface area rather than volume: Let C be a curve that lies entirely on one side of a line l in the plane. If C is rotated about l, then the area of the resulting
> The centroid of a curve can be found by a process similar to the one we used for finding the centroid of a region. If C is a curve with length L, then the centroid is (x, y) where / Here we assign appropriate limits of integration, and ds is as defined i
> Use the Theorem of Pappus to find the volume of the given solid. The solid obtained by rotating the triangle with vertices (2, 3), (2, 5), and (5, 4) about the x-axis
> Use the Theorem of Pappus to find the volume of the given solid. A cone with height h and base radius r
> Use the Theorem of Pappus to find the volume of the given solid. A sphere of radius r
> If x is the x-coordinate of the centroid of the region that lies under the graph of a continuous function f, where a (ex + d)f(x) dx = (cã + d) [* f(x) dx %3D
> A rectangle R with sides a and b is divided into two parts R1 and R2 by an arc of a parabola that has its vertex at one corner of R and passes through the opposite corner. Find the centroids of both R1and R2. R2 Ry
> Find the centroid of the region shown, not by integration, but by locating the centroids of the rectangles and triangles and using additivity of moments. -2 i 2 X -1 2.
> Find the centroid of the region shown, not by integration, but by locating the centroids of the rectangles and triangles and using additivity of moments. yA 2 1- -1 1 2.
> Prove that the centroid of any triangle is located at the point of intersection of the medians.
> Use a graph to find approximate x-coordinates of the points of intersection of the curves y = ex and y = 2 - x2. Then find (approximately) the centroid of the region bounded by these curves.
> Find the centroid of the region bounded by the curves y = x3 - x and y = x2 - 1. Sketch the region and plot the centroid to see if your answer is reasonable.
> Use Simpson’s Rule to estimate the centroid of the region shown. y 4 4 8 x 2. 2.
> Calculate the moments Mx and My and the center of mass of a lamina with the given density and shape. p= 6 y 4 -2
> Calculate the moments Mx and My and the center of mass of a lamina with the given density and shape. - p = 4 yA 3 2
> Find the centroid of the region bounded by the given curves. х+у—2, х — у? 2, х— у
> Find the centroid of the region bounded by the given curves. y = x', x + y = 2, y= 0
> Find the centroid of the region bounded by the given curves. у — sin x, у — сos x, х — 0, х— п/4 TT
> Find the centroid of the region bounded by the given curves. у — 2 — х*, у — х
> A function f is defined by that is, its coefficients are c2n = 1 and c2n+1 = 2 for all n > 0. Find the interval of convergence of the series and find an explicit formula for f(x). f(x) = 1 + 2x + x² + 2x³ + x* + . ||
> Find the centroid of the region bounded by the given curves. y у —х, х— у? x², x=y*
> Sketch the region bounded by the curves, and visually estimate the location of the centroid. Then find the exact coordinates of the centroid. y = sin x, y = 0, 0<x<T
> Sketch the region bounded by the curves, and visually estimate the location of the centroid. Then find the exact coordinates of the centroid. у —е", у—0, х— 0, х— 1
> Sketch the region bounded by the curves, and visually estimate the location of the centroid. Then find the exact coordinates of the centroid. y = Vx, y=0, x= 4 X = 4
> Sketch the region bounded by the curves, and visually estimate the location of the centroid. Then find the exact coordinates of the centroid. у — 2х, у— 0, х— 1 y
> The masses mi are located at the points Pi. Find the moments Mx and My and the center of mass of the system. т — 5, т, — 4, тз — 3, т, — 6; P.(-4, 2), Р.0, 5), Р:(3, 2), Р.(1, —2)
> The masses mi are located at the points Pi. Find the moments Mx and My and the center of mass of the system. т, — 4, тз — 2, тз — 4; P (2, — 3), Р.(-3, 1), P:(3, 5)
> The function A defined by is called an Airy function after the English mathematician and astronomer Sir George Airy (1801–1892). (a) Find the domain of the Airy function. (b) Graph the first several partial sums on a common screen. (c)
> A metal plate was found submerged vertically in seawater, which has density 64 lb/ft3. Measurements of the width of the plate were taken at the indicated depths. Use Simpson’s Rule to estimate the force of the water against the plate.
> A swimming pool is 20 ft wide and 40 ft long and its bottom is an inclined plane, the shallow end having a depth of 3 ft and the deep end, 9 ft. If the pool is full of water, find the hydro static force on (a) the shallow end, (b) the deep end, (c) one o
> A dam is inclined at an angle of 30° from the vertical and has the shape of an isosceles trapezoid 100 ft wide at the top and 50 ft wide at the bottom and with a slant height of 70 ft. Find the hydrostatic force on the dam when it is full of water.
> A cube with 20-cm-long sides is sitting on the bottom of an aquarium in which the water is one meter deep. Find the hydrostatic force on (a) the top of the cube and (b) one of the sides of the cube.
> A vertical dam has a semicircular gate as shown in the figure. Find the hydrostatic force against the gate. ]} 2 m `water level 12 m 4 m
> A trough is filled with a liquid of density 840 kg/m3. The ends of the trough are equilateral triangles with sides 8 m long and vertex at the bottom. Find the hydrostatic force on one end of the trough.
> A milk truck carries milk with density 64.6 lb/ft3 in a horizontal cylindrical tank with diameter 6 ft. (a) Find the force exerted by the milk on one end of the tank when the tank is full. (b) What if the tank is half full?
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. 2а h
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. a a
> The function J1 defined by is called the Bessel function of order 1. (a) Find its domain. (b) Graph the first several partial sums on a common screen. (c) If your CAS has built-in Bessel functions, graph J1 on the same screen as the partial sums in part
> (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate the accuracy of the approximation / when x lies in the given interval. (c) Check your result in part (b) by graphing / S
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. 4 ft
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. 4 m
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. -2 m
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. 4 m
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. 1 4
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. 2 ft
> A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an integral and evaluate it. 3 ft
> A tank is 8 m long, 4 m wide, 2 m high, and contains kerosene with density 820 kg/m3 to a depth of 1.5 m. Find (a) the hydrostatic pressure on the bottom of the tank, (b) the hydrostatic force on the bottom, and (c) the hydrostatic force on one end of th
> An aquarium 5 ft long, 2 ft wide, and 3 ft deep is full of water. Find (a) the hydrostatic pressure on the bottom of the aquarium, (b) the hydrostatic force on the bottom, and (c) the hydrostatic force on one end of the aquarium.
> The graph of the concentration function c(t) is shown after a 7-mg injection of dye into a heart. Use Simpson’s Rule to estimate the cardiac output. (mg/L) 4 0 2 4 6 8 10 12 14 í(seconds) 2.
> After a 5.5-mg injection of dye, the readings of dye concentration, in mg/L, at two-second intervals are as shown in the table. Use Simpson’s Rule to estimate the cardiac output. t c(t) t c(1) 0.0 10 4.3 2 4.1 12 2.5 4 8.9 14 1.2 8

