Question: Let P (x1, y1) be a point
Let P (x1, y1) be a point on the parabola y2 = 4px with focus F (p, 0). Let a be the angle between the parabola and the line segment FP, and let β be the angle between the horizontal line y = y' and the parabola as in the figure. Prove that a = β. (Thus, by a principle of geometrical optics, light from a source placed at F will be reflected along a line parallel to the x-axis. This explains why paraboloids, the surfaces obtained by rotating parabolas about their axes, are used as the shape of some automobile headlights and mirrors for telescopes.)
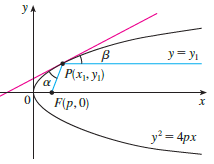
Transcribed Image Text:
y 4 у. y= yı P(x, yı) a F(p,0) y² = 4px
> Verify the given linear approximation at a = 0. Then determine the values of for which the linear approximation is accurate to within 0.1. ex ≈ 1 + x
> Verify the given linear approximation at a = 0. Then determine the values of for which the linear approximation is accurate to within 0.1. 1/ (1 + 2x)4 ≈ 1 - 8x
> Verify the given linear approximation at a = 0. Then determine the values of for which the linear approximation is accurate to within 0.1. tan x ≈ x
> Verify the given linear approximation at a = 0. Then determine the values of for which the linear approximation is accurate to within 0.1. 式
> Find the linear approximation of the function g (x) = 3√1 + x at a = 0 and use it to approximate the numbers 3√0.95 and 3√1.1. Illustrate by graphing g and the tangent line.
> Draw a diagram showing two perpendicular lines that intersect on the y-axis and are both tangent to the parabola y = x2. Where do these lines intersect?
> Find the linear approximation of the function f (x) = √1 - x at a = 0 and use it to approximate the numbers √0.9 and √0.99. Illustrate by graphing f and the tangent line.
> Find the linearization L (x) of the function at a. f (x) = x3/4, a = 16
> Find the linearization L (x) of the function at a. f (x) = cos x, a = π/2
> Find the linearization L (x) of the function at a. f (x) = ln x a = 1
> Find the linearization L (x) of the function at a. f (x) = x4 + 3x2, a = -1
> The table shows the population of Nepal (in millions) as of June 30 of the given year. Use a linear approximation to estimate the population at midyear in 1989. Use another linear approximation to predict the population in 2010. 1985 1990 1995 2000
> Differentiate the function. f (x) = sin (ln x)
> Atmospheric pressure P decreases as altitude h increases. At a temperature of 150C, the pressure is 101.3 kilopascals (kPa) at sea level, 87.1 kPa at h = 1 km, and 74.9 kPa at h = 2 km. Use a linear approximation to estimate the atmospheric pressure at a
> Explain why the natural logarithmic function y = ln x is used much more frequently in calculus than the other logarithmic functions y = logax.
> Find points P and Q on the parabola y = 1 -x2 so that the triangle ABC formed by the x-axis and the tangent lines at P and Q is an equilateral triangle. (See the figure.) y A P. B
> The figure shows the graphs of f, f', and f''. Identify each curve, and explain your choices. у. a b
> For which positive numbers is it true that ax > 1 + x for all x?
> Suppose f is a function that satisfies the equation f (x + y) = f (x) + f (y) + x2y + xy2 for all real numbers x and y. Suppose also that limx→0 f (x)/x = 1 (a). Find a (0). (b). Find f'(0). (c). Find f'(x).
> Water is flowing at a constant rate into a spherical tank. Let V (t) be the volume of water in the tank and H (t) be the height of the water in the tank at time t. (a). What are the meanings of V'(t) and H'(t)? Are these derivatives positive, negative, o
> Let T and N be the tangent and normal lines to the ellipse x2/9 + y2/4= 1 at any point P on the ellipse in the first quadrant. Let xT and yr be the x- and y-intercepts of T and xN and yN be the intercepts of N. As P moves along the ellipse in the first q
> (a). The figure shows an isosceles triangle ABC with ∠B = ∠C. The bisector of angle B intersects the side AC at the point P. Suppose that the base BC remains fixed but the altitude |AM| of the triangle approaches 0, so
> (a). If we start from 00 latitude and proceed in a westerly direction, we can let T (x) denote the temperature at the point at any given time. Assuming that T is a continuous function of x, show that at any fixed time there are at least two diametrically
> A fixed point of a function f is a number c in its domain such that f (c) = c. (The function doesn’t move c; it stays fixed.) (a). Sketch the graph of a continuous function with domain [0, 1] whose range also lies in [0, 1]. Locate a fixed point of f. (b
> The figure shows a rotating wheel with radius 40 cm and a connecting rod AP with length 1.2 m. The pin P slides back and forth along the -axis as the wheel rotates counter clockwise at a rate of 360 revolutions per minute. (a). Find the angular velocit
> Sketch the region in the plane defined by each of the following equations. (a) [x]² + [y]² = 1 (b) [x]² – []° = 3 (c) [r + y]² = 1 (d) [x] + [y] = 1
> Evaluate limx→0 |2x -1|- |2x + 1|/x
> A tangent line is drawn to the hyperbola xy = c at a point P. (a). Show that the midpoint of the line segment cut from this tangent line by the coordinate axes is P. (b). Show that the triangle formed by the tangent line and the coordinate axes always ha
> The graphs of a function f and its derivative f' are shown. Which is bigger, f' (-1) or f"(1)? у.
> The figure shows a point P on the parabola and the point Q where the perpendicular bisector of OP intersects the y-axis. As P approaches the origin along the parabola, what happens to Q? Does it have a limiting position? If so, find it. y y=x P
> Show that the tangent lines to the parabola y = ax2 + bx + c at any two points with x-coordinates p and q must intersect at a point whose -coordinate is halfway between p and q.
> Find the point where the curves y = x3 – 3x + 4 and y = 3 (x2 – x) are tangent to each other, that is, have a common tangent line. Illustrate by sketching both curves and the common tangent.
> The figure shows a circle with radius 1 inscribed in the parabola y = x2. Find the center of the circle. y y= x?
> Draw a graph of f and use it to make a rough sketch of the antiderivative that passes through the origin. f(x) = Vx4 – 2x2 + 2 – 2, -3 <I<3
> Draw a graph of f and use it to make a rough sketch of the antiderivative that passes through the origin. sin x f(x) = 1+ x?"
> The graph of the velocity function of a particle is shown in the figure. Sketch the graph of a position function.
> The graph of a function f is shown. Which graph is an antiderivative of f and why? a
> Let f (x) = x4 – 2x2. (a). Use the definition of a derivative to find f'(x) and f"(x). (b). On what intervals is f increasing or decreasing? (c). On what intervals is f concave upward or concave downward?
> If f'(x) = e-x2, what can you say about f?
> For what values of a and b is the line 2x + y = b tangent to the parabola y = ax2 when x = 2?
> Sketch the graph of a function that satisfies all of the given conditions. f'(x) > 0 if |x| < 2, f'(x) < 0 if |x| > 2, f'(-2) = 0, lim |f'(x) | = ∞, f"(x) > 0 if x # 2
> Sketch the graph of a function that satisfies all of the given conditions. f'(1) = f'(-1) = 0, f'(x) < 0 if |x| < 1, f'(x) > 0 if 1 < |x|< 2, f'(x) = -1 if |x|> 2, f"(x) < 0 if –2 <x< 0, inflection point (0, 1)
> Sketch the graph of a function that satisfies all of the given conditions. f'(0) = f'(2) = f'(4) = 0, f'(x) > 0 if x < 0 or 2 <x< 4, f'(x) < 0 if 0 <x< 2 or x> 4, f"(x) > 0 if 1 < x< 3, f"(x) < 0 if x < 1 or x > 3
> Sketch the graph of a function that satisfies all of the given conditions. f'(x) > 0 for all x # 1, vertical asymptote x = 1, f"(x) > 0 if x < 1 or x> 3, f"(x) < 0 if 1 <x<3
> Sketch the graph of a function that satisfies all of the given conditions. f'(0) = f'(4) = 0, f'(x) > 0 if x < 0, f'(x) < 0 if 0 < x < 4 or if x > 4, f"(x) > 0 if 2 < x< 4, f"(x) < O if x < 2 or x>4
> Sketch the graph of a function whose first derivative is always negative and whose second derivative is always positive.
> Sketch the graph of a function whose first and second derivatives are always negative.
> The president announces that the national deficit is increasing, but at a decreasing rate. Interpret this statement in terms of a function and its derivatives.
> (a). Sketch a curve whose slope is always positive and increasing. (b). Sketch a curve whose slope is always positive and decreasing. (c). Give equations for curves with these properties.
> Estimate the value of f'(a) by zooming in on the graph off. Then differentiate f to find the exact value of f'(a) and compare with your estimate. f (x) = 1/√x, a = 4
> If limx→a [f (x) + g (x)] = 2 and limx→a [f (x) - g (x)] = 1, find limx→a [f (x) g (x)].
> If f is a differentiable function and g (x) = x f (x), use the definition of a derivative to show that g'(x) = x f'(x) + f (x).
> For what value of does the equation e2x = k√x have exactly one solution?
> If y = ((x/√a2 – 1) – (2/√a2 – 1) arctan sin x/a + (√a2 – 1) + cos x) show that y' = 1/a + cos x.
> If f and g are differentiable functions with f (0) = g (0) = 0 and g'(0) ≠0, show that f(x) _ f'(0) lim g(x) g'(0)
> If [[x]] denotes the greatest integer function, find limx→∞ x/[[x]].
> Find the values of the constants a and b such that limx→0 3√ax + b – 2/x = 5/12
> Show that dn/dxn = eax sin bx) = rneaxs sin (bx + nθ) where a and b are positive numbers, r2 = a2 + b2, and θ = tan-1(b/a).
> Tangent lines T1 and T2 are drawn at two points P1 and P2 on the parabola y = x2 and they intersect at a point P. Another tangent line T is drawn at a point between P1 and P2; it intersects T1 at Q1 and T2 at Q2. Show that | PQ.| | P | PQ:| 1
> Find all values of a such that f is continuous on R: Jx +1 if x< a f(x) = |x? - if x>a
> Find a cubic function y = ax2 + bx2 + cx + d whose graph has horizontal tangents at the points (-2, 6) and (2, 6).
> If f is differentiable at a, where a > 0, evaluate the following limit in terms of f'(a): f(x) – f(a) lim VI - Va x,
> If f (x) = limt→x sec t – sec x/t - x, find the value of f'(π/4).
> Show that d/dx (sin2 x/ 1 + cot x + cos2x/1 + tan x) = -cos 2x
> Find numbers a and b such that limx→1 √ax + b – 2/x = 1
> Evaluate limx→1 3√x – 1/√x - 1
> Bézier curves are used in computer-aided design and are named after the French mathematician Pierre Bézier (1910–1999), who worked in the automotive industry. A cubic Bézier curve is determined by
> The tangent line approximation L (x) is the best first-degree (linear) approximation f (x) to near x = a because f (x) and L (x) have the same rate of change (derivative) at a. For a better approximation than a linear one, let’s try a s
> Certain combinations of the exponential functions, ex and e-x arise so frequently in mathematics and its applications that they deserve to be given special names. This project explores the properties of functions called hyperbolic functions. The hyperbol
> State each differentiation rule both in symbols and in words. (a). The Power Rule (b). The Constant Multiple Rule (c). The Sum Rule (d). The Difference Rule (e). The Product Rule (f). The Quotient Rule (g). The Chain Rule
> (a). Suppose the horizontal distance between P and Q is 100 ft. Write equations in a, b, and that will ensure that the track is smooth at the transition points. (b). Solve the equations in part (a) for a, b, and c to find a formula for f (x). (c). Plot L
> Suppose the curve y = x4 + ax3 + bx2 + cx + d has a tangent line when x = 0 with equation y = 2x + 1 and a tangent line when x = 1 with equation y = 2 – 3x. Find the values of a, b, c, and d.
> The solution in Problem 1 might look smooth, but it might not feel smooth because the piecewise defined function [consisting of L1 (x) for x 100] doesn’t have a continuous second derivative. So you decide to improve the design by using
> An approach path for an aircraft landing is shown in the figure and satisfies the following conditions: (i). The cruising altitude is h when descent starts at a horizontal distance from touchdown at the origin. (ii). The pilot must maintain a constant
> (a). What does it mean to say that the line x = a is a vertical asymptote of the curve y = f (x)? Draw curves to illustrate the various possibilities. (b). What does it mean to say that the line y = L is a horizontal asymptote of the curve y = f (x)? Dra
> Describe several ways in which a limit can fail to exist. Illustrate with sketches.
> (a). Define an antiderivative of f. (b). What is the antiderivative of a velocity function? What is the antiderivative of an acceleration function?
> (a). What does the sign of f'(x) tell us about f? (b). What does the sign of f"(x) tell us about f?
> Describe several ways in which a function can fail to be differentiable. Illustrate with sketches.
> (a). What does it mean for f to be differentiable at a? (b). What is the relation between the differentiability and continuity of a function? (c). Sketch the graph of a function that is continuous but not differentiable at a =2.
> Define the second derivative of f. If f (t) is the position function of a particle, how can you interpret the second derivative?
> Define the derivative f'(a). Discuss two ways of interpreting this number.
> Find the parabola with equation y = ax2 + bx whose tangent line at (1, 1) has equation y = 3x - 2.
> If y = f (x) and x changes from x1 to x2, write expressions for the following. (a). The average rate of change of y with respect to x over the interval [x1, x2]. (b). The instantaneous rate of change of y with respect to x at x = x1.
> State the following Limit Laws. (a). Sum Law (b). Difference Law (c). Constant Multiple Law (d). Product Law (e). Quotient Law (f). Power Law (g). Root Law
> State the derivative of each function. (a). y = xn (b). y = ex (c). y = ax (d). y = ln x (e). y = logax (f). y = sin x (g). y = cos x (h). y = tan x (i). y = y = csc x (j). y = sec x (k). y = cot x (l). y = sin-1 x (m). y = cos-1 x (n). y = tan-1 x
> Which of the following curves have vertical asymptotes? Which have horizontal asymptotes? (a). y = x4 (b). y = sin x (c). y = tan x (d). y = ex (e). y = ln x (f). y = 1/x (g). y = √x
> (a). What does it mean for f to be continuous at a? (b). What does it mean for f to be continuous on the interval (∞,∞)? What can you say about the graph of such a function?
> Write an expression for the linearization of, f at a.
> How do you find the slope of a tangent line to a parametric curve x = f (t), y = g (t)?
> (a). Explain how implicit differentiation works. When should you use it? (b). Explain how logarithmic differentiation works. When should you use it?
> (a). How is the number e defined? (b). Express e as a limit. (c). Why is the natural exponential function y = ex used more often in calculus than the other exponential functions y = ax? (d). Why is the natural logarithmic function y = ln x used more oft
> Explain what each of the following means and illustrate with a sketch. (a) lim f(x) = L (b) lim f(x) = L エ→ (c) lim f(r) = L エ→a (d) lim f(x) = 0 エ→ %3D (e) lim f(x) = L
> Find an equation of the tangent line to the curve y = x√x that is parallel to the line y = 1 + 3x.
> Find the limit. limr→9 √r/ (r -9)4
> Find the limit. limt→2 t2 – 4/t3 - 8
> Find the limit. limh→0 (h – 1)3 + 1/h
> Find the limit. limx→1 x2 – 9/x2 + 2x -3
> Find the limit. limx→-3 x2 – 9/x2 + 2x - 3
> Let C (t) be the total value of US currency (coins and banknotes) in circulation at time t. The table gives values of this function from 1980 to 2000, as of September 30, in billions of dollars. Interpret and estimate the value of C'(1990). t 1980 1

