Question: Level curves for barometric pressure (in millibars)
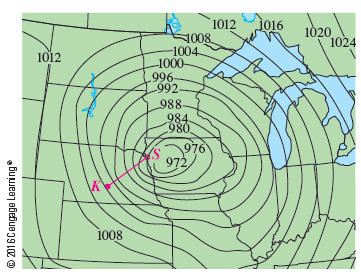
Level curves for barometric pressure (in millibars) are shown for 6:00 am on a day in November. A deep low with pressure 972 mb is moving over northeast Iowa. The distance along the red line from K (Kearney, Nebraska) to S (Sioux City, Iowa) is 300 km. Estimate the value of the directional derivative of the pressure function at Kearney in the direction of Sioux City. What are the units of the directional derivative?
Transcribed Image Text:
1012 j016 1020 1024 1008 -1004 -1000- 996- 992- 988 984 980 1012 976 972 1008 ® 2016Cengage Learring
> An economist wanted to learn more about total compensation packages. She conducted a survey of 858 workers and asked all to report their hourly wages or salaries, their total benefits, and whether the companies they worked for produced goods or services.
> Low back pain is a common medical problem that sometimes results in disability and absence from work. Any method of treatment that decreases absence would be welcome by individuals and insurance companies. A randomized control study (published in Annals
> An apple juice manufacturer has developed a new product—a liquid concentrate that produces 1 liter of apple juice when mixed with water. The product has several attractive features. First, it is more convenient than bottled apple juice, which is the way
> If t (x, y) = x2 + y2 - 4x, find the gradient vector Vg = t (1, 2) and use it to find the tangent line to the level curve t (x, y) = 1 at the point (1, 2). Sketch the level curve, the tangent line, and the gradient vector.
> If f (x, y) = xy, find the gradient vector =f (3, 2) and use it to find the tangent line to the level curve f (x, y) = 6 at the point (3, 2). Sketch the level curve, the tangent line, and the gradient vector.
> Use the Chain Rule to find dz/dt or dw/dt. х — у x + 2y' x = e"", y = e-
> Use a tree diagram to write out the Chain Rule for the given case. Assume all functions are differentiable. w = f (x, y, z), where x = x (u, v), y = y (u, v), z = z (u, v)
> Find the directional derivative of the function at the given point in the direction of the vector v. f (x, y, z) = xy2 tan-1z, (2, 1, 1), v = 1, 1, 1
> Find the directional derivative of the function at the given point in the direction of the vector v. f(x, y, 2) — х'у + у?г, (1,2, 3), v%3D(2, —1, 2)
> Find the local maximum and minimum values and saddle point(s) of the function. If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. f(x, y) = x² + y* +
> Suppose that the equation F (x, y, z) = 0 implicitly defines each of the three variables x, y, and z as functions of the other two: z = f (x, y), y = t (x, z), x = h (y, z). If F is differentiable and Fx, Fy, and Fz are all nonzero, show that дх дх
> The speed of sound traveling through ocean water with salinity 35 parts per thousand has been modeled by the equation C = 1449.2 + 4.6T - 0.055T2 + 0.00029T3 + 0.016D where C is the speed of sound (in meters per second), T is the temperature (in degree
> At what points does the normal line through the point (1, 2, 1) on the ellipsoid 4x2 + y2 + 4z2 = 12 intersect the sphere x2 + y2 + z2 = 102?
> Show that every plane that is tangent to the cone x2 + y2 = z2 passes through the origin.
> Show that the ellipsoid 3x2 + 2y2 + z2 = 9 and the sphere x2 + y2 + z2 - 8x - 6y - 8z + 24 = 0 are tangent to each other at the point (1, 1, 2). (This means that they have a common tangent plane at the point.)
> Are there any points on the hyperboloid x2 - y2 - z2 = 1 where the tangent plane is parallel to the plane z = x + y?
> At what point on the ellipsoid x2 + y2 + 2z2 = 1 is the tangent plane parallel to the plane x + 2y + z = 1?
> Use a computer to graph the surface, the tangent plane, and the normal line on the same screen. Choose the domain carefully so that you avoid extraneous vertical planes. Choose the viewpoint so that you get a good view of all three objects. xyz = 6, (1,
> Use a computer to graph the surface, the tangent plane, and the normal line on the same screen. Choose the domain carefully so that you avoid extraneous vertical planes. Choose the viewpoint so that you get a good view of all three objects. xy + yz + zx
> Find equations of (a) the tangent plane and (b) the normal line to the given surface at the specified point. x4 + y4 + z4 = 3x2y2z2, (1, 1, 1)
> Find the local maximum and minimum values and saddle point(s) of the function. If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. f(x, y) = y(e* – 1)
> Find equations of (a) the tangent plane and (b) the normal line to the given surface at the specified point. x + y + z = exyz, (0, 0, 1)
> Find equations of (a) the tangent plane and (b) the normal line to the given surface at the specified point. xy + yz + zx = 5, (1, 2, 1)
> Find equations of (a) the tangent plane and (b) the normal line to the given surface at the specified point. xy2z3 = 8, (2, 2, 1)
> Find equations of (a) the tangent plane and (b) the normal line to the given surface at the specified point. x = y2 + z2 + 1, (3, 1, -1)
> Find equations of (a) the tangent plane and (b) the normal line to the given surface at the specified point. 2 (x – 2)2 + (y – 1)2 + (z – 3)2 = 10, (3, 3, 5)
> Sketch the gradient vector ∆ f (4, 6) for the function f whose level curves are shown. Explain how you chose the direction and length of this vector. yA -5 6- -3 (4, 6) 4- 5 2+ 2 4 6. 3-
> Shown is a topographic map of Blue River Pine Provincial Park in British Columbia. Draw curves of steepest descent from point A (descending to Mud Lake) and from point B. Blue River o Blue River Mud Ca Blue River Pine Provincial Park Mud Creek Snfok
> Suppose you are climbing a hill whose shape is given by the equation z = 1000 - 0.005x2 - 0.01y2, where x, y, and z are measured in meters, and you are standing at a point with coordinates (60, 40, 966). The positive x-axis points east and the positive y
> Equation 6 is a formula for the derivative dy/dx of a function defined implicitly by an equation F (x, y) = 0, provided that F is differentiable and Fy ± 0. Prove that if F has continuous second derivatives, then a formula for the second de
> If f is homogeneous of degree n, show that fx (tx, ty) = tn-1 f (x, y)
> Find the local maximum and minimum values and saddle point(s) of the function. If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. f(x, y) = (x – y)(1
> Suppose that the directional derivatives of f (x, y) are known at a given point in two nonparallel directions given by unit vectors u and v. Is it possible to find ∆f at this point? If so, how would you do it?
> (a). Two surfaces are called orthogonal at a point of intersection if their normal lines are perpendicular at that point. Show that surfaces with equations F (x, y, z) = 0 and G (x, y, z) = 0 are orthogonal at a point P where ∆F ≠ 0 and ∆G ≠ 0 if and onl
> (a). The plane y + z = 3 intersects the cylinder x2 + y2 = 5 in an ellipse. Find parametric equations for the tangent line to this ellipse at the point (1, 2, 1). (b). Graph the cylinder, the plane, and the tangent line on the same screen.
> Find parametric equations for the tangent line to the curve of intersection of the paraboloid z = x2 + y2 and the ellipsoid 4x2 + y2 + z2 = 9 at the point (-1, 1, 2).
> Show that the pyramids cut off from the first octant by any tangent planes to the surface xyz − 1 at points in the first octant must all have the same volume.
> Find an equation of the plane that passes through the point (1, 2, 3) and cuts off the smallest volume in the first octant.
> Find the local maximum and minimum values and saddle point(s) of the function. If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. f (x, y) — ху — 2х
> Where does the normal line to the paraboloid z = x2 + y2 at the point (1, 1, 2) intersect the paraboloid a second time?
> Three alleles (alternative versions of a gene) A, B, and O determine the four blood types A (AA or AO), B (BB or BO), O (OO), and AB. The Hardy-Weinberg Law states that the proportion of individuals in a population who carry two different alleles is P =
> The Shannon index (sometimes called the Shannon-Wiener index or Shannon-Weaver index) is a measure of diversity in an ecosystem. For the case of three species, it is defined as H = -p1 ln p1 - p2 ln p2 - p3 ln p3 where pi is the proportion of species i
> A model for the yield Y of an agricultural crop as a function of the nitrogen level N and phosphorus level P in the soil (measured in appropriate units) is Y (N, P) = kNPe-N-P where k is a positive constant. What levels of nitrogen and phosphorus resul
> If the length of the diagonal of a rectangular box must be L, what is the largest possible volume?
> A rectangular building is being designed to minimize heat loss. The east and west walls lose heat at a rate of 10 units/m2 per day, the north and south walls at a rate of 8 units/m2 per day, the floor at a rate of 1 unit/m2 per day, and the roof at a rat
> A cardboard box without a lid is to have a volume of 32,000 cm3. Find the dimensions that minimize the amount of cardboard used.
> Near a buoy, the depth of a lake at the point with coordinates (x, y) is z = 200 + 0.02x2 - 0.001y3, where x, y, and z are measured in meters. A fisherman in a small boat starts at the point s80, 60d and moves toward the buoy, which is located at (0, 0).
> Find all points at which the direction of fastest change of the function f (x, y) = x2 + y2 - 2x - 4y is i + j.
> (a). Show that a differentiable function f decreases most rapidly at x in the direction opposite to the gradient vector, that is, in the direction of 2=f (x). (b). Use the result of part (a) to find the direction in which the function f (x, y) = x4y - x2
> One side of a triangle is increasing at a rate of 3 cm/s and a second side is decreasing at a rate of 2 cm/s. If the area of the triangle remains constant, at what rate does the angle between the sides change when the first side is 20 cm long, the second
> Find the dimensions of the box with volume 1000 cm3 that has minimal surface area.
> Find the maximum volume of a rectangular box that is inscribed in a sphere of radius r.
> Find three positive numbers whose sum is 12 and the sum of whose squares is as small as possible.
> Find three positive numbers whose sum is 100 and whose product is a maximum.
> Find the points on the surface y2 = 9 + xz that are closest to the origin.
> Find the points on the cone z2 = x2 + y2 that are closest to the point (4, 2, 0).
> Find the point on the plane x - 2y + 3z = 6 that is closest to the point (0, 1, 1).
> Find the shortest distance from the point (2, 0, -3) to the plane x + y + z = 1.
> If a function of one variable is continuous on an interval and has only one critical number, then a local maximum has to be an absolute maximum. But this is not true for functions of two variables. Show that the function has exactly one critical point,
> Use the level curves in the figure to predict the location of the critical points of f and whether f has a saddle point or a local maximum or minimum at each critical point. Explain your reasoning. Then use the Second Derivatives Test to confirm your pre
> For functions of one variable it is impossible for a continuous function to have two local maxima and no local minimum. But for functions of two variables such functions exist. Show that the function has only two critical points, but has local maxima a
> Find the absolute maximum and minimum values of f on the set D. f (x, y) = x3 - 3x - y3 + 12y, D is the quadrilateral whose vertices are (-2, 3), (2, 3), (2, 2), and (-2, -2)
> Find the absolute maximum and minimum values of f on the set D. f(x, y) = 2x³ + y*, D= {(x, y) | x² + y² < 1}
> Find the absolute maximum and minimum values of f on the set D. f(x, y) = xy², D= {(x, y) | x > 0, y > 0, x² + y? < 3}
> Find the absolute maximum and minimum values of f on the set D. f(x, y) = x² + 2y² D = {(x, y) | 0 < x< 2,0 < y< 3} — 2х — 4у + 1,
> Find the absolute maximum and minimum values of f on the set D. f(x, y) = x² + xy + y? – 6y, D = {(x, y) | –3 <I< 3,0 < y< 5}
> Find the absolute maximum and minimum values of f on the set D. f(x, y) = x² + y² + x*y + 4, D = {(r, y) | |x| < 1, |y| < 1}
> Find the absolute maximum and minimum values of f on the set D. f (x, y) = x + y - xy, D is the closed triangular region with vertices (0, 0), (0, 2), and (4, 0)
> Find the absolute maximum and minimum values of f on the set D. f (x, y) = x2 + y2 - 2x, D is the closed triangular region with vertices (2, 0), (0, 2), and (0, -2)
> Use a graphing device as in Example 4 (or Newton’s method or solve numerically using a calculator or computer) to find the critical points of f correct to three decimal places. Then classify the critical points and find the highest or l
> Use the level curves in the figure to predict the location of the critical points of f and whether f has a saddle point or a local maximum or minimum at each critical point. Explain your reasoning. Then use the Second Derivatives Test to confirm your pre
> Use a graphing device as in Example 4 (or Newton’s method or solve numerically using a calculator or computer) to find the critical points of f correct to three decimal places. Then classify the critical points and find the highest or l
> Use a graphing device as in Example 4 (or Newton’s method or solve numerically using a calculator or computer) to find the critical points of f correct to three decimal places. Then classify the critical points and find the highest or l
> Use a graphing device as in Example 4 (or Newton’s method or solve numerically using a calculator or computer) to find the critical points of f correct to three decimal places. Then classify the critical points and find the highest or l
> Use a graph or level curves or both to estimate the local maximum and minimum values and saddle point(s) of the function. Then use calculus to find these values precisely. f(x, y) = sin x + sin y + cos(x + y), 0 < x< T/4, 0 < y</4
> Use a graph or level curves or both to estimate the local maximum and minimum values and saddle point(s) of the function. Then use calculus to find these values precisely. f(x, y) = sin x + sin y + sin(x + y), 0 <x< 27, 0 <y< 27
> Use a graph or level curves or both to estimate the local maximum and minimum values and saddle point(s) of the function. Then use calculus to find these values precisely. f(x, y) = (x – y)e²-y²
> Use a graph or level curves or both to estimate the local maximum and minimum values and saddle point(s) of the function. Then use calculus to find these values precisely. f(x, y) = x² + y² +x-?y-2
> Show that f (x, y) = x2ye-x2-y2 has maximum values at (±1, 1/ 2 ) and minimum values at (±1, -1/ 2 ). Show also that f has infinitely many other critical points and D = 0 at each of them. Which of them give rise to maximum values? Minimum values? Saddl
> Show that f (x, y) = x2 + 4y2 - 4xy + 2 has an infinite number of critical points and that D = 0 at each one. Then show that f has a local (and absolute) minimum at each critical point.
> Find the local maximum and minimum values and saddle point(s) of the function. If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. f(x, y) = sin x sin
> The contour map shows the average maximum temperature for November 2004 (in 0C). Estimate the value of the directional derivative of this temperature function at Dubbo, New South Wales, in the direction of Sydney. What are the units? 100 200 300 (Di
> Let p(t) = f (t(t), h(t)), where f is differentiable, t(2) = 4, g'(2) = -3, h(2) = 5, h'(2) = 6, fx (4, 5) = 2, fy (4, 5) = 8. Find p'(2).
> Find the directional derivative of the function at the given point in the direction of the vector v. t (u, v) = u2e-v, (3, 0), v = 3i + 4 j
> Find the directional derivative of the function at the given point in the direction of the vector v. f(x, y) = (1, 2), v = (3, 5) .2 + y
> (a). Find the gradient of f. (b). Evaluate the gradient at the point P. (c). Find the rate of change of f at P in the direction of the vector u. f(x, y, 2) 3 у'е"»,, Р(), 1, —1), %3D u= 13. 13 13
> Use the Chain Rule to find dz/dt or dw/dt. w = In /x² + y? + z?, x= sin t, y = cos t, z = tan t %3D
> Use the figure to estimate Du f (2, 2). yA (2, 2) u Vf(2, 2)
> Assume that all the given functions have continuous second-order partial derivatives. If u = f (x, y), where x = es cos t and y = es sin t, show that u ar au -2s e ду?
> Use the Chain Rule to find dz/dt or dw/dt. w = xey/z, x = t2, y = 1 - t, z = 1 + 2t
> Assume that all the given functions have continuous second-order partial derivatives. Show that any function of the form is a solution of the wave equation. z = f (x + at) + t (x – at) az a'z at? [Hint: Let u = x + at, v = x – at.
> The voltage V in a simple electrical circuit is slowly decreasing as the battery wears out. The resistance R is slowly increasing as the resistor heats up. Use Ohm’s Law, V = IR, to find how the current I is changing at the moment when R = 400 Ω, I = 0.0
> The length ℓ, width w, and height h of a box change with time. At a certain instant the dimensions are ℓ = 1 m and w = h = 2 m, and ℓ, and w are increasing at a rate of 2 m/s while h is decreasing at a rate of 3 m/s. At that instant find the rates at whi
> Find the local maximum and minimum values and saddle point(s) of the function. If you have three-dimensional graphing software, graph the function with a domain and viewpoint that reveal all the important aspects of the function. f(x, y) = xy + ey
> Use Equation 6 to find dy/dx. Equation 6: cos (xy) = 1 + sin y aF dy F. dx F,
> Use the Chain Rule to find the indicated partial derivatives. u = xe", x= a°B, y = B'y, t= ya; au du du da' aß' ay when a — -1, B — 2, у %3D 1
> Use the Chain Rule to find the indicated partial derivatives. p + q N p= u + vw, q- v + uw,r= w + uv; %3D p +r' aN aN aN when u = 2, v = 3, w = 4 ne dv' dw
> Use the Chain Rule to find the indicated partial derivatives. P = Vu? + v? + w², u= xe', v= ye", w = e*"; aP ap when x = 0, y = 2 ax ay
> Use the Chain Rule to find the indicated partial derivatives. = xy + yz + zx, x=r cos 0, y = r sin 0, z = = re; dw dw when r= 2,0 = 7/2 ar' a0
> Use the Chain Rule to find the indicated partial derivatives. T = 2и + u = pq r, v= pvg r; aT aT aT when p = 2, q = 1, r = 4 ap' ag' ar

