Question: Magnetostatics treats the “source current” (the one
Magnetostatics treats the “source current†(the one that sets up the ï¬eld) and the “recipient current†(the one that experiences the force) so asymmetrically that it is by no means obvious that the magnetic force between two current loops is consistent with Newton’s third law. Show, starting with the Biot-Savart law (Eq. 5.34) and the Lorentz force law (Eq. 5.16), that the force on loop 2 due to loop 1 (Fig. 5.61) can be written as
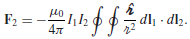
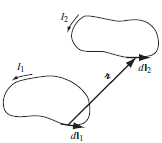
In this form, it is clear that F2=-F1, since rˆ changes direction when the roles of 1 and 2 are interchanged. (If you seem to be getting an “extra†term, it will help to note that dl2 · rˆ = dr.)
> A long circular cylinder of radius R carries a magnetization M = ks2 φˆ, where k is a constant, s is the distance from the axis, and φˆ is the usual azimuthal unit vector (Fig. 6.13). Find the
> An infinitely long circular cylinder carries a uniform magnetization M parallel to its axis. Find the magnetic field (due to M) inside and outside the cylinder.
> Of the following materials, which would you expect to be paramagnetic and which diamagnetic: aluminum, copper, copper chloride (CuCl2), carbon, lead, nitrogen (N2), salt (NaCl), sodium, sulfur, water? (Actually, copper is slightly diamagnetic; otherwise
> A uniform current density J = J0 zˆ fills a slab straddling the yz plane, from x = −a to x = +a. A magnetic dipole m = m0 xˆ is situated at the origin. (a) Find the force on the dipole, using Eq. 6.3. (b) Do the same for a dipole pointing in the y directi
> Derive Eq. 6.3. [Here’s one way to do it: Assume the dipole is an infinitesimal square, of side ε (if it’s not, chop it up into squares, and apply the argument to each one). Choose axes as s
> Find the force of attraction between two magnetic dipoles, m1 and m2, oriented as shown in Fig. 6.7, a distance r apart, (a) using Eq. 6.2, and (b) using Eq. 6.3.
> You are asked to referee a grant application, which proposes to determine whether the magnetization of iron is due to “Ampère” dipoles (current loops) or “Gilbert” dipoles (separated magnetic monopoles). The experiment will involve a cylinder of iron (ra
> Calculate the volume integral of the function T z2 over the tetrahedron with corners at (0,0,0), (1,0,0), (0,1,0), and (0,0,1).
> A magnetic dipole m is imbedded at the center of a sphere (radius R) of linear magnetic material (permeability μ). Show that the magnetic field inside the sphere (0 < r ≤ R) is / What is the field outside the sphere?
> At the interface between one linear magnetic material and another, the magnetic field lines bend (Fig. 6.32). Show that tan θ2/ tan θ1 μ2/μ1, assuming there is no free current at the
> Compare Eqs. 2.15, 4.9, and 6.11. Notice that if ρ, P, and M are uniform, the same integral is involved in all three: Therefore, if you happen to know the electric field of a uniformly charged object, you can immediately write d
> Notice the following parallel: Thus, the transcription turns an electrostatic problem into an analogous magnetostatic one. Use this, together with your knowledge of the electrostatic results, to rederive (a) the magnetic field inside a uni
> Imagine two charged magnetic dipoles (charge q, dipole moment m), constrained to move on the z axis (same as Problem 6.23(a), but without gravity). Electrically they repel, but magnetically (if both m’s point in the z direction) they attract. (a) Find th
> A familiar toy consists of donut-shaped permanent magnets (magnetization parallel to the axis), which slide frictionlessly on a vertical rod (Fig. 6.31). Treat the magnets as dipoles, with mass md and dipole moment m. (a) If you put two back-to-back magn
> In Prob. 6.4, you calculated the force on a dipole by “brute force.” Here’s a more elegant approach. First write B(r) as a Taylor expansion about the center of the loop: where r0 is the position of th
> (a) Show that the energy of a magnetic dipole in a magnetic field B is [Assume that the magnitude of the dipole moment is fixed, and all you have to do is move it into place and rotate it into its final orient
> How would you go about demagnetizing a permanent magnet (such as the wrench we have been discussing, at point c in the hysteresis loop)? That is, how could you restore it to its original state, with M = 0 at I = 0?
> Starting from the Lorentz force law, in the form of Eq. 5.16, show that the torque on any steady current distribution (not just a square loop) in a uniform field B is m × B.
> Calculate the surface integral of the function in Ex. 1.7, over the bot- tom of the box. For consistency, let “upward” be the positive direction. Does the surface integral depend only on the boundary line for this function? What is the total flux over the
> Find the angle between the body diagonals of a cube.
> On the basis of the naïve model presented in Sect. 6.1.3, estimate the magnetic susceptibility of a diamagnetic metal such as copper. Compare your answer with the empirical value in Table 6.1, and comment on any discrepancy.
> A sphere of linear magnetic material is placed in an otherwise uniform magnetic field B0. Find the new field inside the sphere. [Hint: See Prob. 6.15 or Prob. 4.23.]
> A current I flows down a long straight wire of radius a. If the wire is made of linear material (copper, say, or aluminum) with susceptibility χm , and the current is distributed uniformly, what is the magnetic field a distance s from the axis? Find all th
> A coaxial cable consists of two very long cylindrical tubes, separated by linear insulating material of magnetic susceptibility χm . A current I flows down the inner conductor and returns along the outer one; in each case, the c
> If J f=0 everywhere, the curl of H vanishes (Eq. 6.19), and we can express H as the gradient of a scalar potential W : H = −∇W. According to Eq. 6.23, then, ∇2 W = (∇ · M), so W obeys Poisson’s equation, with M as the “source.” This opens up all the mach
> For the bar magnet of Prob. 6.9, make careful sketches of M, B, and H, assuming L is about 2a. Compare Prob. 4.17.
> Suppose the field inside a large piece of magnetic material is B0, so that H0 = (1/μ0)B0 − M, where M is a “frozen-in” magnetization. (a) Now a small spherical cavity is h
> An infinitely long cylinder, of radius R, carries a “frozen-in” magnetization, parallel to the axis, M = ks zˆ, where k is a constant and s is the distance from the axis; there is no free current anywhere. Find the magnetic field inside and outside the cyl
> In Sect, 6.2.1, we began with the potential of a perfect dipole (Eq. 6.10), whereas in fact we are dealing with physical dipoles. Show, by the method of Sect. 4.2.3, that we nonetheless get the correct macroscopic field.
> An iron rod of length L and square cross section (side a) is given a uniform longitudinal magnetization M, and then bent around into a circle with a narrow gap (width w), as shown in Fig. 6.14. Find the magnetic field at the center of the
> Calculate the line integral of the function / from the origin to the point (1,1,1) by three different routes: (a) (0, 0, 0) → (1, 0, 0) → (1, 1, 0) → (1, 1, 1). (b) (0, 0, 0) → (0, 0, 1) → (0, 1, 1) → (1, 1, 1). (c) The direct straight line. (d) What is
> Calculate the torque exerted on the square loop shown in Fig. 6.6, due to the circular loop (assume r is much larger than a or b). If the square loop is free to rotate, what will its equilibrium orientation be?
> Find the magnetic field at point P for each of the steady current configurations shown in Fig. 5.23.
> (a) Find the magnetic field at the center of a square loop, which carries a steady current I . Let R be the distance from center to side (Fig. 5.22). (b) Find the field at the center of a regular n-sided polygon, carrying a
> For a configuration of charges and currents confined within a volume V, show that where p is the total dipole moment. [Hint: evaluate /
> A thin glass rod of radius R and length L carries a uniform surface charge σ . It is set spinning about its axis, at an angular velocity ω. Find the magnetic field at a distance s((R from the axis, in the xy plane (Fi
> Using Eq. 5.88, calculate the average magnetic field of a dipole over a sphere of radius R centered at the origin. Do the angular integrals first. Compare your answer with the general theorem in Prob. 5.59. Explain the discr
> A uniformly charged solid sphere of radius R carries a total charge Q, and is set spinning with angular velocity ω about the z axis. (a) What is the magnetic dipole moment of the sphere? (b) Find the average magnetic field within the sphere (see Prob. 5.5
> (a) A phonograph record carries a uniform density of “static electricity” σ . If it rotates at angular velocity ω, what is the surface current density K at a distance r from the center? (b) A uniformly charged solid sphere, of radius R and total charge Q
> (a) Prove that the average magnetic field, over a sphere of radius R, due to steady currents inside / where m is the total dipole moment of the sphere. Contrast the electrostatic result, Eq. 3.105. [This is tough, so I’l
> A thin uniform donut, carrying charge Q and mass M , rotates about its axis as shown in Fig. 5.64. (a) Find the ratio of its magnetic dipole moment to its angular momentum. This is called the gyromagnetic ratio (or magnetomechanical ratio). (b) What is t
> Prove that the curl of a gradient is always zero. Check it for function (b) in Prob. 1.11.
> A magnetic dipole / is situated at the origin, in an otherwise uniform magnetic field / Show that there exists a spherical surface, centered at the origin, through which no magnetic field lines pass. Find the radius of this sphere, and sketch the field li
> Prove the following uniqueness theorem: If the current density J is specified throughout a volume V, and either the potential A or the magnetic field B is specified on the surface S bounding V, then the magnetic field itself is uniquely determined throughout
> Just as ∇ · B = 0 allows us to express B as the curl of a vector potential (B = ∇ × A), so ∇ · A = 0 permits us to write A itself as the curl of a “higher” potential: A = ∇ × W. (And this hierarchy can be extended ad infinitum.) (a) Find the general formu
> (a) Construct the scalar potential U(r) for a “pure” magnetic dipole m. (b) Construct a scalar potential for the spinning spherical shell (Ex. 5.11). [Hint: for r > R this is a pure dipole field, as you can see by comparing Eqs. 5.69 and 5.87.] (c) Try do
> Another way to fill in the “missing link” in Fig. 5.48 is to look for a magnetostatic analog to Eq. 2.21. The obvious candidate would be / (a) Test this formula for the simplest possible caseâ
> (a) One way to fill in the “missing link” in Fig. 5.48 is to exploit the analogy between the defining equations for and Maxwell’s equations for / Evidently A depends on
> Consider a plane loop of wire that carries a steady current I ; we want to calculate the magnetic field at a point in the plane. We might as well take that point to be the origin (it could be inside or outside the loop). The shape of the w
> (a) If it is uniformly distributed over the surface, what is the surface current density K ? (b) If it is distributed in such a way that the volume current density is inversely proportional to the distance from the axis, what is J(s)?
> Suppose you wanted to find the field of a circular loop (Ex. 5.6) at a point r that is not directly above the center (Fig. 5.60). You might as well choose your axes so that r lies in the yz plane at (0, y, z). The source poi
> Prove that the divergence of a curl is always zero. Check it for function va in Prob. 1.15.
> Use Eq. 5.41 to obtain the magnetic field on the axis of the rotating disk in Prob. 5.37(a). Show that the dipole field (Eq. 5.88), with the dipole moment you found in Prob. 5.37, is a good approximation if z ((R.
> The magnetic field on the axis of a circular current loop (Eq. 5.41) is far from uniform (it falls off sharply with increasing z). You can produce a more nearly uniform field by using two such loops a distance d apart (Fig. 5.59). (a) Find the field (B) as
> Use the Biot-Savart law (most conveniently in the form of Eq. 5.42 appropriate to surface currents) to find the field inside and outside an infinitely long solenoid of radius R, with n turns per unit length, c
> Consider the motion of a particle with mass m and electric charge qe in the field of a (hypothetical) stationary magnetic monopole qm at the origin: / (a) Find the acceleration of qe, expressing your answer in terms of q, qm , m, r (the p
> Calculate the magnetic force of attraction between the northern and southern hemispheres of a spinning charged spherical shell (Ex. 5.11). [Answer: (π/4)μ0σ 2ω2 R4.]
> A circularly symmetrical magnetic field (B depends only on the distance from the axis), pointing perpendicular to the page, occupies the shaded region in Fig. 5.58. If the total flux / is zero, show that a charged particle
> A plane wire loop of irregular shape is situated so that part of it is in a uniform magnetic field B (in Fig. 5.57 the field occupies the shaded region, and points perpendicular to the plane of the loop). The loop carries a
> A current I flows to the right through a rectangular bar of conducting material, in the presence of a uniform magnetic field B pointing out of the page (Fig. 5.56). (a) If the moving charges are positive, in which direction
> It may have occurred to you that since parallel currents attract, the current within a single wire should contract into a tiny concentrated stream along the axis. Yet in practice the current typically distributes itself quite uniformly over the wire. How
> Suppose that the magnetic field in some region has the form B = kz xˆ (where k is a constant). Find the force on a square loop (side a), lying in the yz plane and centered at the origin, if it carries a current I , flowing counterclockwise, when you look d
> Calculate the Laplacian of the following functions: (a) Ta = x 2 + 2xy + 3z + 4. (b) Tb = sin x sin y sin z. (c) Tc = e−5x sin 4y cos 3z. (d) v = x 2 xˆ + 3xz2 yˆ− 2xz zˆ.
> Analyze the motion of a particle (charge q, mass m) in the magnetic field of a long straight wire carrying a steady current I . (a) Is its kinetic energy conserved? (b) Find the force on the particle, in cylindrical coordinates, with I along the z axis. (
> I worked out the multipole expansion for the vector potential of a line current because that’s the most common type, and in some respects the easiest to handle. For a volume current J: (a) Write down the multipole expansion, analogous t
> (a) A phonograph record of radius R, carrying a uniform surface charge σ , is rotating at constant angular velocity ω. Find its magnetic dipole moment. (b) Find the magnetic dipole moment of the spinning spherical shell in Ex. 5.11. Show that for points
> Find the exact magnetic field a distance z above the center of a square loop of side w, carrying a current I . Verify that it reduces to the field of a dipole, with the appropriate dipole moment, when z ((w.
> A circular loop of wire, with radius R, lies in the xy plane (centered at the origin) and carries a current I running counterclockwise as viewed from the positive z axis. (a) What is its magnetic dipole moment? (b) What is the (approximate) magnetic field
> Show that the magnetic field of a dipole can be written in coordinate- free form:
> Prove Eq. 5.78, using Eqs. 5.63, 5.76, and 5.77. [Suggestion: I’d set up Cartesian coordinates at the surface, with z perpendicular to the surface and x parallel to the current.]
> (a) Check Eq. 5.76 for the configuration in Ex. 5.9. (b) Check Eqs. 5.77 and 5.78 for the configuration in Ex. 5.11.
> (a) Complete the proof of Theorem 2, Sect. 1.6.2. That is, show that any diver genceless vector field F can be written as the curl of a vector potential A. What you have to do is find Ax , Ay , and Az such that (i) ∂ Az/∂ y ∂ Ay /∂ z Fx ; (ii) ∂ Ax /∂ z
> Use the results of Ex. 5.11 to find the magnetic field inside a solid sphere, of uniform charge density ρ and radius R, that is rotating at a constant angular velocity ω.
> (a) Check product rule (iv) (by calculating each term separately) for the functions A = x xˆ + 2y yˆ + 3z zˆ; B = 3y xˆ − 2x yˆ. (b) Do the same for product rule (ii). (c) Do the same for rule (vi).
> In 1897, J. J. Thomson “discovered” the electron by measuring the charge-to-mass ratio of “cathode rays” (actually, streams of electrons, with charge q and mass m) as follows: (a) First he passed the beam through uniform crossed electric and magnetic fiel
> Suppose you want to define a magnetic scalar potential U (Eq. 5.67) in the vicinity of a current-carrying wire. First of all, you must stay away from the wire itself / but that’s not enough. Show, by applying AmpÃ
> (a) Check that Eq. 5.65 is consistent with Eq. 5.63, by applying the divergence. (b) Check that Eq. 5.65 is consistent with Eq. 5.47, by applying the curl. (c) Check that Eq. 5.65 is consistent with Eq. 5.64, by applying the Laplacian.
> Find the vector potential above and below the plane surface current in Ex. 5.8.
> (a) By whatever means you can think of (short of looking it up), find the vector potential a distance s from an infinite straight wire carrying a current I . Check that ∇ · A = 0 and ∇ × A = B. (b) Find the magnetic potential inside the wire, if it has rad
> If B is uniform, show that / works. That is, check that / Is this result unique, or are there other functions with the same divergence and curl?
> What current density would produce the vector potential, A=k φˆ (where k is a constant), in cylindrical coordinates?
> Find the magnetic vector potential of a finite segment of straight wire carrying a current I . [Put the wire on the z axis, from z1 to z2, and use Eq. 5.66.] Check that your answer is consistent with Eq. 5.37.
> Suppose there did exist magnetic monopoles. How would you modify Maxwell’s equations and the force law to accommodate them? If you think there are several plausible options, list them, and suggest how you might decide experimentally which one is right.
> Is Ampère’s law consistent with the general rule (Eq. 1.46) that divergence-of-curl is always zero? Show that Ampère’s law cannot be valid, in general, outside magnetostatics. Is there any such “defect” in the other three Maxwell equations?
> Derive the three quotient rules.
> (a) Find the density ρ of mobile charges in a piece of copper, assuming each atom contributes one free electron. [Look up the necessary physical constants.] (b) Calculate the average electron velocity in a copper wire 1 mm in diameter, carrying a current
> Find and sketch the trajectory of the particle in Ex. 5.2, if it starts at the origin with velocity (a) v(0) = (E/B)yˆ, (b) v(0) = (E/2B)yˆ, (c) v(0) = (E/B)(yˆ + zˆ).
> In calculating the current enclosed by an Amperian loop, one must, in general, evaluate an integral of the form The trouble is, there are infinitely many surfaces that share the same boundary line. Which one are we supposed to use?
> Show that the magnetic field of an infinite solenoid runs parallel to the axis, regardless of the cross-sectional shape of the coil, as long as that shape is constant along the length of the solenoid. What is the magnitude of the field, inside and outside o
> A large parallel-plate capacitor with uniform surface charge σ on the upper plate and σ on the lower is moving with a constant speed v, as shown in Fig. 5.43. (a) Find the magnetic field between the plates and also ab
> Two long coaxial solenoids each carry current I, but in opposite directions, as shown in Fig. 5.42. The inner solenoid (radius a) has n1 turns per unit length, and the outer one (radius b) has n2. Find B in each of the three regions: (i) inside the inner
> A thick slab extending from z=-a to z=+a (and infinite in the x and y directions) carries a uniform volume current / (Fig. 5.41). Find the magnetic field, as a function of z, both inside and outside the slab.
> A steady current I flows down a long cylindrical wire of radius a (Fig. 5.40). Find the magnetic field, both inside and outside the wire, if (a) The current is uniformly distributed over the outside surface of the wire. (b)
> Suppose you have two infinite straight line charges λ, a distance d apart, moving along at a constant speed v (Fig. 5.26). How great would v have to be in order for the magnetic attraction to balance the electrical repulsion?
> Use the result of Ex. 5.6 to calculate the magnetic field at the center of a uniformly charged spherical shell, of radius R and total charge Q, spinning at constant angular velocity ω.
> Prove product rules (ii) and (vi). Refer to Prob. 1.22 for the definition of (A · ∇)B.
> Find the magnetic field at point P on the axis of a tightly wound solenoid (helical coil) consisting of n turns per unit length wrapped around a cylindrical tube of radius a and carrying current I (Fig. 5.25). Express your answer in terms
> (a) Find the force on a square loop placed as shown in Fig. 5.24(a), near an infinite straight wire. Both the loop and the wire carry a steady current I . (b) Find the force on the triangular loop in Fig. 5.24(b).
> A particle of charge q enters a region of uniform magnetic field B (pointing into the page). The field deflects the particle a distance d above the original line of flight, as shown in Fig. 5.8.
> A dipole p is a distance r from a point charge q, and oriented so that p makes an angle θ with the vector r from q to p. (a) What is the force on p? (b) What is the force on q?

