Question: On a dry surface, the braking distances (
On a dry surface, the braking distances (in feet), from 60 miles per hour to a complete stop, of a sedan can be approximated by a normal distribution, as shown in the figure at the left.
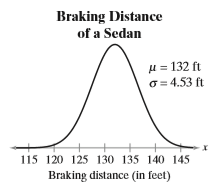
What braking distance of a sedan represents the first quartile?
Transcribed Image Text:
Braking Distance of a Sedan H = 132 ft O = 4.53 ft 115 120 125 130 135 140 145 Braking distance (in feet)
> Find the indicated binomial probabilities. If convenient, use technology or Table 2 in Appendix B. Sixty-two percent of U.S. adults get news on social media sites. You randomly select five U.S. adults. Find the probability that the number of U.S. adults
> In Exercise 25(b), would a sample size of 369 be acceptable? Explain.
> You wish to estimate, with 95% confidence, the population proportion of U.S. adults who have taken or planned to take a winter vacation in a recent year. Your estimate must be accurate within 5% of the population proportion. a. No preliminary estimate i
> In Exercise 22, does it seem possible that the population proportion could be within 1% of the point estimate? Explain.
> In Exercise 19, does it seem possible that the population proportion could equal 0.75? Explain. From Exercise 19: In a survey of 1035 U.S. adults, 745 say they want the U.S. to play a leading or major role in global affairs.
> Let p be the population proportion for the situation. a. Find point estimates of p and q, b. construct 90% and 95% confidence intervals for p, and c. interpret the results of part (b) and compare the widths of the confidence intervals. In a survey of
> Let p be the population proportion for the situation. a. Find point estimates of p and q, b. construct 90% and 95% confidence intervals for p, and c. interpret the results of part (b) and compare the widths of the confidence intervals. In a survey of
> Let p be the population proportion for the situation. a. Find point estimates of p and q, b. construct 90% and 95% confidence intervals for p, and c. interpret the results of part (b) and compare the widths of the confidence intervals. In a survey of
> Let p be the population proportion for the situation. a. Find point estimates of p and q, b. construct 90% and 95% confidence intervals for p, and c. interpret the results of part (b) and compare the widths of the confidence intervals. In a survey of
> You research the heights of top-rated roller coasters and find that the population mean is 160 feet. In Exercise 17, does the t-value fall between -t0.95 and t0.95?
> In a random sample of 36 top-rated roller coasters, the average height is 165 feet and the standard deviation is 67 feet. Construct a 90% confidence interval form. Interpret the results.
> Find the indicated binomial probabilities. If convenient, use technology or Table 2 in Appendix B. Eighty-eight percent of U.S. civilian full-time employees have access to medical care benefits. You randomly select nine civilian full-time employees. Find
> a. find the margin of error for the values of c, s, and n, and b. construct the confidence interval for µ using the t-distribution. Assume the population is normally distributed. c = 0.99, s = 16.5, n = 20, x = 25.2
> a. find the margin of error for the values of c, s, and n, and b. construct the confidence interval for µ using the t-distribution. Assume the population is normally distributed. c = 0.98, s = 0.9, n = 12, x = 6.8
> a. find the margin of error for the values of c, s, and n, and b. construct the confidence interval for µ using the t-distribution. Assume the population is normally distributed. c = 0.95, s = 1.1, n = 25, x = 3.5
> a. find the margin of error for the values of c, s, and n, and b. construct the confidence interval for µ using the t-distribution. Assume the population is normally distributed. c = 0.90, s = 25.6, n = 16, x = 72.1
> Find the critical value tc for the level of confidence c and sample size n. c = 0.99, n = 30
> Find the critical value tc for the level of confidence c and sample size n. c = 0.98, n = 15
> Find the critical value tc for the level of confidence c and sample size n. c = 0.95, n = 24
> Find the critical value tc for the level of confidence c and sample size n. c = 0.80, n = 10
> Determine the minimum sample size required to be 99% confident that the sample mean driving distance to work is within 2 miles of the population mean driving distance to work. Use the population standard deviation from Exercise 2.
> Determine the minimum sample size required to be 95% confident that the sample mean waking time is within 10 minutes of the population mean waking time. Use the population standard deviation from Exercise 1.
> Find the indicated binomial probabilities. If convenient, use technology or Table 2 in Appendix B. Thirty-nine percent of U.S. adults have a gun in their home. You randomly select 12 U.S. adults. Find the probability that the number of U.S. adults who ha
> Use the confidence interval to find the margin of error and the sample mean. (7.428, 7.562)
> You wish to estimate the mean winning time for Boston Marathon Women’s Open Division champions. The estimate must be within 0.13 hour of the population mean. Determine the minimum sample size required to construct a 99% confidence interval for the popula
> The winning times (in hours) for a sample of 30 randomly selected Boston Marathon Women’s Open Division champions are shown in the table at the left. a. Find the point estimate of the population mean. b. Find the margin of error for a 95% confidence l
> Refer to the data set in Exercise 3. Assume the population of times spent checking email is normally distributed. Construct a 95% confidence interval for a. the population variance and b. the population standard deviation. Interpret the results.
> In a survey of 1018 U.S. adults, 753 say that the energy situation in the United States is very or fairly serious. a. Find the point estimate for the population proportion. b. Construct a 90% confidence interval for the population proportion. Interpret
> You research the salaries of senior-level chemical engineers and find that the population mean is $131,935. In Exercise 4, does the t-value fall between -t0.95 and t0.95?
> In a random sample of 12 senior-level chemical engineers, the mean annual earnings was $133,326 and the standard deviation was $36,729. Assume the annual earnings are normally distributed and construct a 95% confidence interval for the population mean an
> The data set represents the amounts of time (in minutes) spent checking email for a random sample of employees at a company. a. Find the sample mean and the sample standard deviation. b. Construct a 90% confidence interval for the population mean. Inte
> The random variable x is normally distributed with mean µ = 18 and standard deviation σ = 7.6. Find the value of x that has 64.8% of the distribution’s area to its right.
> The random variable x is normally distributed with mean µ = 18 and standard deviation σ = 7.6. Find the value of x that has 88.3% of the distribution’s area to its left
> Find the indicated binomial probabilities. If convenient, use technology or Table 2 in Appendix B. Fifty-three percent of U.S. adults want to lose weight. You randomly select eight U.S. adults. Find the probability that the number of U.S. adults who want
> The random variable x is normally distributed with mean µ = 18 and standard deviation σ = 7.6. Find each probability. a. P(x > 20) b. P(0 < x < 5) c. P(x < 9 or x > 27)
> The mean per capita daily water consumption in a village in Bangladesh is about 83 liters per person and the standard deviation is about 11.9 liters per person. Random samples of size 50 are drawn from this population and the mean of each sample is deter
> The per capita disposable income for residents of a U.S. city in a recent year is normally distributed, with a mean of about $44,000 and a standard deviation of about $2450. Random samples of size 8 are drawn from the population and the mean of each samp
> The per capita disposable income for residents of a U.S. city in a recent year is normally distributed, with a mean of about $44,000 and a standard deviation of about $2450. Between what two values does the middle 60% of disposable incomes lie?
> The per capita disposable income for residents of a U.S. city in a recent year is normally distributed, with a mean of about $44,000 and a standard deviation of about $2450. Out of 800 residents, about how many would you expect to have a disposable incom
> The per capita disposable income for residents of a U.S. city in a recent year is normally distributed, with a mean of about $44,000 and a standard deviation of about $2450. Find the probability that the disposable income of a resident is more than $45,0
> Determine whether you can use a normal distribution to approximate the binomial distribution. If you can, use the normal distribution to approximate the indicated probabilities and sketch their graphs. If you cannot, explain why and use a binomial distri
> Determine whether you can use a normal distribution to approximate the binomial distribution. If you can, use the normal distribution to approximate the indicated probabilities and sketch their graphs. If you cannot, explain why and use a binomial distri
> Use the normal curves shown. Which normal curve has the greatest mean? Explain your reasoning. B 80 90 100 110 120 130 140
> Use the normal curve to estimate the mean and standard deviation. 40 45 50 55 60 65 70 75
> Determine whether the experiment is a binomial experiment. If it is, identify a success, specify the values of n, p, and q, and list the possible values of the random variable x. If it is not a binomial experiment, explain why. A fair coin is tossed repe
> Use the normal curve to estimate the mean and standard deviation. 5 10 15 20 25
> A population and sample size are given. a. Find the mean and standard deviation of the population. b. List all samples (with replacement) of the given size from the population and find the mean of each. c. Find the mean and standard deviation of the s
> On a dry surface, the braking distances (in feet), from 60 miles per hour to a complete stop, of a sedan can be approximated by a normal distribution, as shown in the figure at the left. What is the longest braking distance of a sedan that can be in the
> On a dry surface, the braking distances (in feet), from 60 miles per hour to a complete stop, of a sedan can be approximated by a normal distribution, as shown in the figure at the left. What is the shortest braking distance of a sedan that can be in th
> On a dry surface, the braking distances (in feet), from 60 miles per hour to a complete stop, of a sedan can be approximated by a normal distribution, as shown in the figure at the left. What braking distance of a sedan represents the 90th percentile?
> On a dry surface, the braking distances (in feet), from 60 miles per hour to a complete stop, of a sedan can be approximated by a normal distribution, as shown in the figure at the left. Find the braking distance of a sedan that corresponds to z = 1.6.
> On a dry surface, the braking distances (in feet), from 60 miles per hour to a complete stop, of a sedan can be approximated by a normal distribution, as shown in the figure at the left. Find the braking distance of a sedan that corresponds to z = -2.75
> Find the positive z-score for which 94% of the distribution’s area lies between -z and z.
> Find the z-score that has 30.5% of the distribution’s area to its right.
> Determine whether the experiment is a binomial experiment. If it is, identify a success, specify the values of n, p, and q, and list the possible values of the random variable x. If it is not a binomial experiment, explain why. Bags of milk chocolate M&M
> Use the Standard Normal Table or technology to find the z-score that corresponds to the cumulative area or percentile. P46
> Use the Standard Normal Table or technology to find the z-score that corresponds to the cumulative area or percentile. P85
> Use the Standard Normal Table or technology to find the z-score that corresponds to the cumulative area or percentile. P2
> Use the Standard Normal Table or technology to find the z-score that corresponds to the cumulative area or percentile. 0.993
> Use the Standard Normal Table or technology to find the z-score that corresponds to the cumulative area or percentile. 0.1
> Use the Standard Normal Table or technology to find the z-score that corresponds to the cumulative area or percentile. 0.4721
> Determine whether any of the events in Exercise 34 are unusual. Explain your reasoning.
> Determine whether any of the events in Exercise 33 are unusual. Explain your reasoning.
> Find the indicated probabilities. If convenient, use technology to find the probabilities. The daily surface concentration of carbonyl sulfide on the Indian Ocean is normally distributed, with a mean of 9.1 picomoles per liter and a standard deviation of
> Find the indicated probabilities. If convenient, use technology to find the probabilities. Yearly amounts of black carbon emissions from cars in India are normally distributed, with a mean of 14.7 gigagrams per year and a standard deviation of 11.5 gigag
> Find the expected net gain to the player for one play of the game. A scratch-off lottery ticket costs $5. The table at the left shows the probability of winning various prizes on the ticket. Prize Probability 1 $100,000 100,000 1 $100 100 $50 50
> Determine whether the random variable x is discrete or continuous. Explain your reasoning. a. Let x represent the number of lightning strikes that occur in Wyoming during the month of June. b. Let x represent the amount of fuel (in gallons) used by a j
> A student’s test grade of 75 represents the 65th percentile of the grades. What percent of students scored higher than 75?
> Identify the population and the sample. Describe the sample data set. A study of 203 infants was conducted to find a link between fetal tobacco exposure and focused attention in infancy.
> Identify the population and the sample. Describe the sample data set. A survey of 1020 U.S. adults found that 42% trust their political leaders.
> Use the Venn diagram to identify the population and the sample. Incomes of Home Owners in Massachusetts Incomes of home owners in Massachusetts with mortgages Incomes of home owners in Massachusetts without mortgages
> Use the Venn diagram to identify the population and the sample. Ages of Adults in the United States Who Own Automobiles Ages of adults in the U.S. who own Honda automobiles Ages of adults in the U.S. who own automobiles made by a company other than H
> Use the Venn diagram to identify the population and the sample. Student Donations at a Food Drive Student donations of canned goods Student donations of other food items
> Use the Venn diagram to identify the population and the sample. Parties of Registered Voters Parties of registered voters who respond to a survey Parties of registered voters who do not respond to a survey
> Determine whether the data set is a population or a sample. Explain your reasoning. The air contamination levels at 20 locations near a factory
> Match the plot with the description of the sample. a. Times (in minutes) it takes a sample of employees to drive to work b. Grade point averages of a sample of students with finance majors c. Top speeds (in miles per hour) of a sample of high-performa
> Why is a sample used more often than a population?
> A study shows that the obesity rate among adolescents has steadily increased since 1988. From this study, a researcher infers that this trend will continue in future years. What is wrong with this type of reasoning?
> Determine whether the data set is a population or a sample. Explain your reasoning. The political party of every U.S. senator
> Use the relative frequency histogram to a. identify the class with the greatest, and the class with the least, relative frequency. b. approximate the greatest and least relative frequencies. c. describe any patterns with the data. Female Fibula Le
> Determine whether the data set is a population or a sample. Explain your reasoning. The age of every fourth person entering a grocery store
> Determine whether the data set is a population or a sample. Explain your reasoning. The final score of each gamer in a tournament
> Determine whether the data set is a population or a sample. Explain your reasoning. The number of wireless devices in each U.S. household
> Determine whether the data set is a population or a sample. Explain your reasoning. The triglyceride levels of 10 patients in a clinic with 50 patients
> Determine whether the data set is a population or a sample. Explain your reasoning. The annual revenue of each store in a shopping mall
> Identify the sample space of the probability experiment and determine the number of outcomes in the event. Draw a tree diagram when appropriate. Experiment: Choosing a month of the year Event: Choosing a month that begins with the letter J
> Find the probability. A card is randomly selected from a standard deck of 52 playing cards. Find the probability that the card is between 4 and 8, inclusive, or is a club.
> A sample of 6500 automobiles found that 1560 of the automobiles were black, 3120 of the automobiles were sedans, and 1170 of the automobiles were black sedans. Find the probability that a randomly chosen automobile from this sample is black or a sedan.
> The weights (in pounds) of the defensive players on a high school football team are shown below. Draw a box-and-whisker plot that represents the data set and describe the shape of the distribution. 173 145 205 192 197 227 156 240 172 208 185 190 167
> A random sample of 250 working adults found that 74% access the Internet at work, 88% access the Internet at home, and 72% access the Internet at both work and home. Find the probability that a person in this sample selected at random accesses the Intern
> Determine whether the events are mutually exclusive. Explain your reasoning. Event A: Randomly select a person who loves cats. Event B: Randomly select a person who owns a dog.
> Determine whether the events are mutually exclusive. Explain your reasoning. Event A: Randomly select a red jelly bean from a jar. Event B: Randomly select a yellow jelly bean from the same jar.
> Your sock drawer has 18 folded pairs of socks, with 8 pairs of white, 6 pairs of black, and 4 pairs of blue. What is the probability, without looking in the drawer, that you will first select and remove a black pair, then select either a blue or a white
> Your roommate has asked you to buy toothpaste and dental rinse, but your roommate did not tell you which brands to get. The store has eight brands of toothpaste and five brands of dental rinse. What is the probability that you will purchase the correct b
> Determine whether the data set is a population or a sample. Explain your reasoning. A survey of 300 people from an auditorium with 13,000 people
> Determine whether the events are independent or dependent. Explain your reasoning. Getting high grades and being awarded an academic scholarship
> Determine whether the events are independent or dependent. Explain your reasoning. Taking a driver’s education course and passing the driver’s license exam
> Determine whether the events are independent or dependent. Explain your reasoning. Selecting an ace from a standard deck of 52 playing cards, and then selecting a jack from the deck without replacing the ace.
> Identify the sample space of the probability experiment and determine the number of outcomes in the event. Draw a tree diagram when appropriate. Experiment: Rolling 2 six-sided dice Event: Getting a sum of 4 or 5
> Find the interquartile range of the data set from Exercise 13. From Exercise 13: 33.0 35.5 37.5 31.0 28.0 29.5 21.0 26.0 24.0 29.5

